Construct Quad Tree

Medium

Uber

13 views

Topics:

TreesRecursionArrays

Given a n * n matrix grid of 0's and 1's only. We want to represent grid with a Quad-Tree.

Return the root of the Quad-Tree representing grid.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

val: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the val to True or False when isLeaf is False, and both are accepted in the answer.
isLeaf: True if the node is a leaf node on the tree or False if the node has four children.

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

Example 1:

Input: grid = [[0,1],[1,0]]
Output: [[0,1],[1,0],[1,1],[1,1],[1,0]]
Explanation: The explanation of this example is shown below:
Notice that 0 represents False and 1 represents True in the photo representing the Quad-Tree.

Example 2:

Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:

Constraints:

n == grid.length == grid[i].length
n == 2^x where 0 <= x <= 6

Construct Quad Tree

Medium

Uber

13 views

Topics:

TreesRecursionArrays

Given a n * n matrix grid of 0's and 1's only. We want to represent grid with a Quad-Tree.

Return the root of the Quad-Tree representing grid.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

val: True if the node represents a grid of 1's or False if the node represents a grid of 0's. Notice that you can assign the val to True or False when isLeaf is False, and both are accepted in the answer.
isLeaf: True if the node is a leaf node on the tree or False if the node has four children.

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

You don't need to read this section for solving the problem. This is only if you want to understand the output format here. The output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

Example 1:

Input: grid = [[0,1],[1,0]]
Output: [[0,1],[1,0],[1,1],[1,1],[1,0]]
Explanation: The explanation of this example is shown below:
Notice that 0 represents False and 1 represents True in the photo representing the Quad-Tree.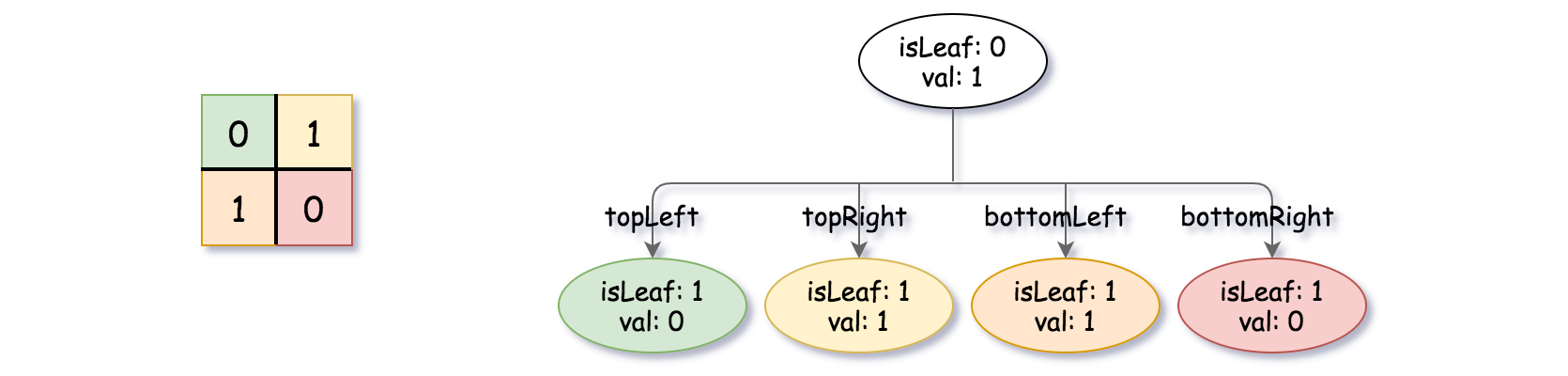

Example 2:

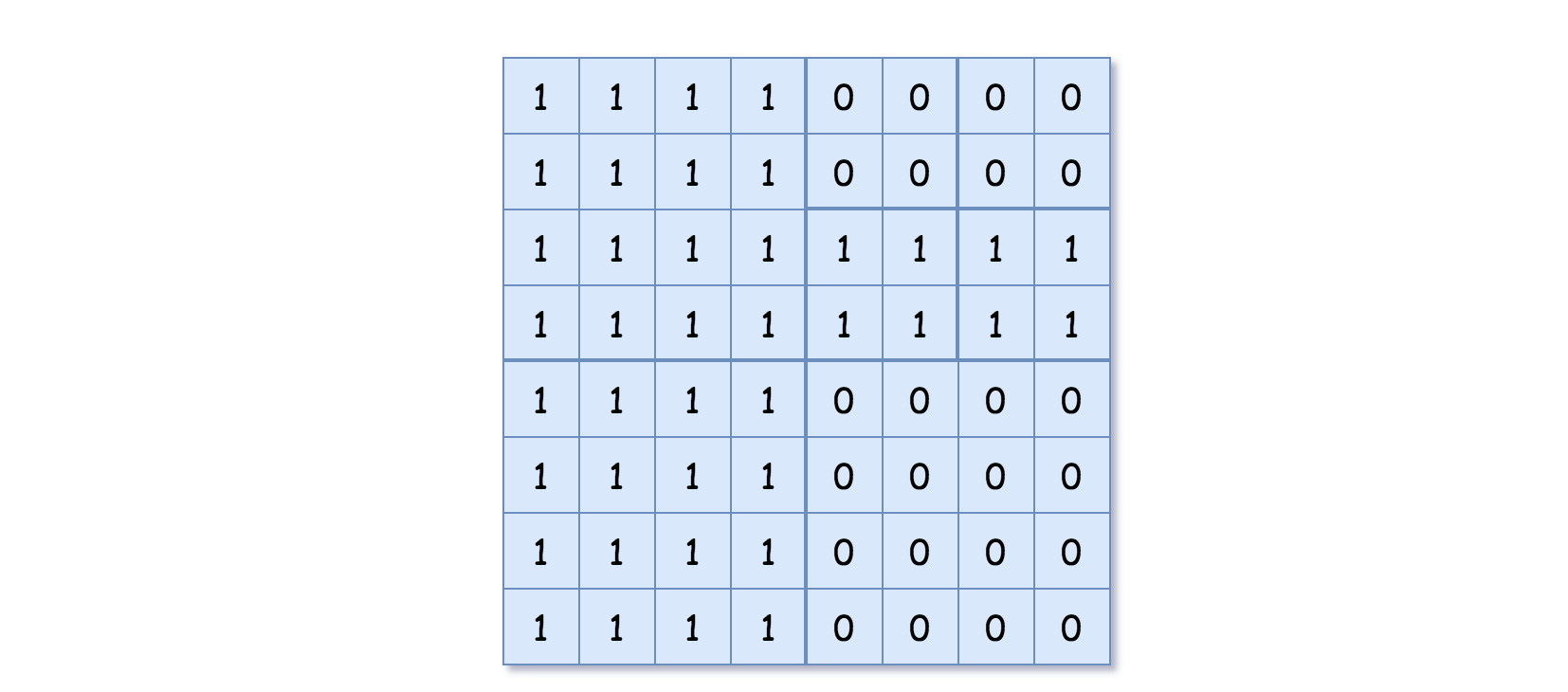
Input: grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
Output: [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Explanation: All values in the grid are not the same. We divide the grid into four sub-grids.
The topLeft, bottomLeft and bottomRight each has the same value.
The topRight have different values so we divide it into 4 sub-grids where each has the same value.
Explanation is shown in the photo below:

Constraints:

n == grid.length == grid[i].length
n == 2^x where 0 <= x <= 6

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum size of the grid (n)?
Is the grid guaranteed to be square (n x n), or could it be rectangular?
If a subgrid contains mixed 0s and 1s, how should I create the corresponding node (specifically, what should its `isLeaf` and `val` be set to)?
Is it permissible to modify the original grid in place, or should I treat it as immutable?
Can I assume that `n` will always be a power of 2?

Brute Force Solution

Approach

To build the Quad Tree with a brute force method, we'll examine every possible square section within the input grid. We determine if each section is uniform by checking if all its values are the same, and create a node based on that determination.

Here's how the algorithm would work step-by-step:

Start by considering the entire input grid as a potential Quad Tree node.
Check if all the values (true or false) within this entire grid are the same. If they are, create a leaf node representing this grid, and the process stops for this branch.
If the values are not all the same, divide the grid into four equal-sized quadrants.
Treat each quadrant as a new, smaller grid and repeat the process from step two. That is, check if all values within the top-left quadrant are the same. If so, create a leaf node. If not, divide this quadrant again into four smaller quadrants.
Continue this division and checking process recursively for each quadrant until you reach a point where all values in a quadrant are the same (making it a leaf node) or the quadrant becomes a single element.
Once all the quadrants have been processed in this way, link the resulting nodes together to form the complete Quad Tree. The initial node represents the entire grid, and its children represent the four quadrants, and so on.

Code Implementation

class Node:
    def __init__(self, is_leaf, value, top_left=None, top_right=None,
                 bottom_left=None, bottom_right=None):
        self.isLeaf = is_leaf
        self.val = value
        self.topLeft = top_left
        self.topRight = top_right
        self.bottomLeft = bottom_left
        self.bottomRight = bottom_right

def construct_quad_tree(grid):
    def build_tree(grid, top_row, top_col, side_length):

        # Check if the current grid section is uniform
        if is_uniform(grid, top_row, top_col, side_length):
            return Node(True, grid[top_row][top_col])

        # If not uniform, divide into four quadrants and construct recursively
        half_side = side_length // 2

        # Recursively construct the top-left quadrant
        top_left_node = build_tree(grid, top_row, top_col, half_side)

        # Recursively construct the top-right quadrant
        top_right_node = build_tree(grid, top_row, top_col + half_side, half_side)

        # Recursively construct the bottom-left quadrant
        bottom_left_node = build_tree(grid, top_row + half_side, top_col, half_side)

        # Recursively construct the bottom-right quadrant
        bottom_right_node = build_tree(grid, top_row + half_side, top_col + half_side, half_side)

        # Create a non-leaf node with the four quadrants as children
        return Node(False, True, top_left_node, top_right_node, bottom_left_node, bottom_right_node)

    def is_uniform(grid, top_row, top_col, side_length):
        first_value = grid[top_row][top_col]
        for row_index in range(top_row, top_row + side_length):
            for col_index in range(top_col, top_col + side_length):
                if grid[row_index][col_index] != first_value:
                    return False
        return True

    grid_size = len(grid)
    return build_tree(grid, 0, 0, grid_size)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n² log n) – The algorithm recursively divides the n x n grid into four quadrants until each quadrant represents a single value. The depth of the recursion is log₄(n²) which is equivalent to log₂(n). At each level of the recursion, we need to check if a quadrant is uniform, which takes O(n²) time in the worst case. Since there are log n levels, the overall time complexity is O(n² log n).

Space Complexity

O(N) – The algorithm's space complexity is primarily determined by the recursive calls. In the worst-case scenario, where the input grid's values alternate in a checkerboard pattern, the algorithm will divide the grid into four quadrants recursively until each quadrant contains only a single element. This leads to a recursion depth of log4(N), where N is the number of elements in the grid (side length of the grid is sqrt(N)). Each recursive call consumes stack space. Because, in the worst case, we create a node for each element, the space will be proportional to the number of nodes in the tree. The quadtree can have, in the worst case, O(N) nodes; thus the space complexity is O(N).

Optimal Solution

Approach

The key is to use recursion and check if each quadrant of the grid has the same value. If it does, we can create a leaf node; otherwise, we recursively build the tree for each quadrant and combine them into a parent node.

Here's how the algorithm would work step-by-step:

Start with the entire grid.
Check if all values within the current section of the grid are the same.
If all values are the same, create a single leaf node representing that value and mark it as a leaf.
If the values are different, divide the current section of the grid into four equal quadrants.
Recursively apply the same process to each of the four quadrants, creating four child nodes.
Create a parent node that links to these four child nodes, representing the subdivided section.

Code Implementation

class Node:
    def __init__(self, value, is_leaf, top_left, top_right, bottom_left, bottom_right):
        self.value = value
        self.is_leaf = is_leaf
        self.top_left = top_left
        self.top_right = top_right
        self.bottom_left = bottom_left
        self.bottom_right = bottom_right

def construct_quad_tree(grid):
    def build_tree(grid, top, left, side_length):
        # Check if the current section of the grid has the same value.
        if all(grid[top + i][left + j] == grid[top][left]
               for i in range(side_length) for j in range(side_length)):
            return Node(grid[top][left], True, None, None, None, None)

        # If values are different, divide into four quadrants.
        half_side = side_length // 2

        # Recursively build the tree for each quadrant.
        top_left_node = build_tree(grid, top, left, half_side)

        top_right_node = build_tree(grid, top, left + half_side, half_side)

        bottom_left_node = build_tree(grid, top + half_side, left, half_side)

        bottom_right_node = build_tree(grid, top + half_side, left + half_side, half_side)

        # Create a parent node linking to the four child nodes.
        # The value is arbitrary since it's not a leaf.
        return Node(0, False, top_left_node, top_right_node, bottom_left_node, bottom_right_node)

    grid_size = len(grid)
    return build_tree(grid, 0, 0, grid_size)

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – The algorithm processes an n x n grid by recursively dividing it into quadrants. In the worst-case scenario where the grid contains alternating values, the recursion continues until individual cells are reached. For each node in the quadtree, checking if a quadrant has uniform values takes O(n²) time in the worst case. Since we potentially need to examine all n² elements in the original grid across multiple levels of recursion, and in the worst case, construct a full quadtree, the overall time complexity can be expressed as O(n²). This is because, in the worst case, we might have to visit each of the n² cells in the grid multiple times during the recursive subdivisions and value checks.

Space Complexity

O(N) – The space complexity is primarily determined by the recursion depth. In the worst case, where the grid has alternating values such that each quadrant always needs further subdivision, the recursion will go down to individual cells. For a grid of size N x N where N is a power of 2, the maximum depth of the recursion is log_2(N). However, each recursive call creates a new QuadTreeNode. In the worst case, the algorithm might create a complete quadtree which can have O(N) nodes, since N is the total number of elements in the input grid. Therefore, the auxiliary space used for the call stack and the QuadTree nodes will be O(N).

Edge Cases

Case	How to Handle
Null or empty input grid	Return null as the root of the quadtree is undefined for an empty grid.
Grid of size 1x1	Create a leaf node with the value of the single element in the grid, setting `isLeaf` to true.
Grid with non-square dimensions (m x n where m != n)	The problem statement specifies n*n grid; the solution should throw an exception or handle this error case appropriately if encountered.
Grid with all elements having the same value (either all 0s or all 1s)	Create a single leaf node with `isLeaf` set to true and the common value as its `val`.
Grid with alternating 0s and 1s (maximum variation)	The solution should recursively divide the grid until it reaches the base case of a 1x1 grid or a uniform subgrid.
Very large grid (e.g., 2^10 x 2^10) that could lead to stack overflow due to deep recursion	Consider iterative solution or techniques to limit recursion depth to prevent stack overflow, perhaps by using helper function to track recursion depth and switch to iteration past some limit.
Invalid input values (values other than 0 or 1)	Throw an IllegalArgumentException if input values other than 0 or 1 are encountered.
Memory constraints with extremely large grids	If memory is a huge concern, external memory algorithms or approximate solutions with limited quadtree depth might be necessary (but are likely outside the scope of a standard interview).