Container With Most Water
Container With Most Water #2 Most Asked
MediumYou are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example 1:
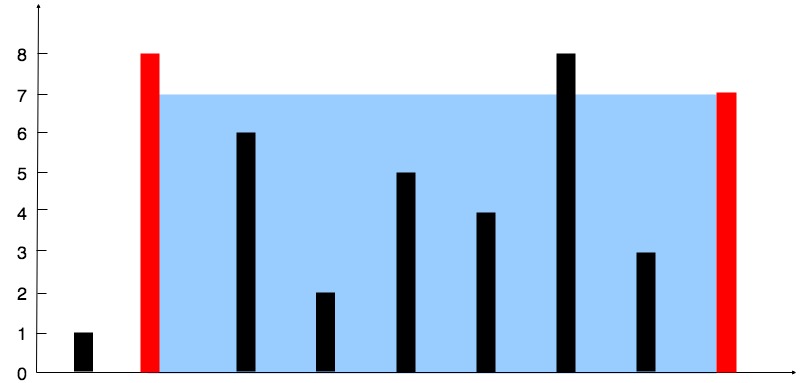
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1] Output: 1
Constraints:
n == height.length2 <= n <= 1050 <= height[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the size of the `height` array, and what is the range of values for the heights themselves?
- Are the heights guaranteed to be non-negative integers, or could they be floats or negative values?
- What should be returned if the input array is empty or contains only one element?
- Can the array contain duplicate height values, and if so, how should they be handled in terms of forming containers?
- Does the problem guarantee that at least two lines will always be present to form a container, or could the array be too small to form any container?
Brute Force Solution
Approach
We want to find the largest container we can form using vertical lines of different heights. The brute force way to do this is to consider every single possible pair of lines that could form a container and see which one holds the most water.
Here's how the algorithm would work step-by-step:
- Pick the very first line.
- Now, consider pairing that first line with every other line, one by one, starting from the second line all the way to the last.
- For each of these pairs, calculate how much water that specific container could hold.
- Keep track of the biggest amount of water you've seen so far.
- Once you've checked all possible containers that use the first line, move on to the second line.
- Now, pair the second line with every line that comes after it (from the third line to the last).
- Again, calculate the water capacity for each of these new containers and update your record if you find a larger one.
- Continue this process, moving to the third line and pairing it with all subsequent lines, then the fourth line, and so on, until you have checked every possible combination of two lines.
- The largest amount of water you've recorded at the end will be your answer.
Code Implementation
def max_area_brute_force(heights):
maximum_water_found = 0
number_of_lines = len(heights)
# Iterate through each line as the left boundary of the container
for left_line_index in range(number_of_lines):
# Iterate through each line to the right of the current left line as the right boundary
for right_line_index in range(left_line_index + 1, number_of_lines):
# Calculate the height of the container, which is limited by the shorter line
container_height = min(heights[left_line_index], heights[right_line_index])
# Calculate the width of the container
container_width = right_line_index - left_line_index
# Calculate the current water volume
current_water_volume = container_height * container_width
# Update the maximum water found if the current container holds more
maximum_water_found = max(maximum_water_found, current_water_volume)
return maximum_water_foundBig(O) Analysis
Optimal Solution
Approach
Imagine you have a set of vertical bars of different heights. We want to find two bars that, when used as the sides of a container, can hold the most water. The optimal approach avoids checking every single pair by cleverly narrowing down the possibilities.
Here's how the algorithm would work step-by-step:
- Start by considering the outermost bars as your initial container.
- Calculate the amount of water this container can hold. This is determined by the shorter of the two bars (since water will spill over the shorter side) and the distance between them.
- Now, decide which of the two bars to move inwards. To potentially hold more water, you should always move the shorter bar inwards. The reason is that moving the taller bar inwards will never increase the container's height (it's limited by the shorter bar anyway), and it will decrease the width, thus reducing the water capacity.
- After moving the shorter bar, recalculate the water capacity with the new pair of bars.
- Keep track of the largest amount of water you've found so far.
- Continue this process of moving the shorter bar inwards and recalculating until the two bars meet.
- The maximum water capacity found during this entire process is your answer.
Code Implementation
def max_area(height_values):
left_pointer = 0
right_pointer = len(height_values) - 1
maximum_water_volume = 0
while left_pointer < right_pointer:
current_height = min(height_values[left_pointer], height_values[right_pointer])
current_width = right_pointer - left_pointer
current_volume = current_height * current_width
# We need to keep track of the largest volume found so far.
maximum_water_volume = max(maximum_water_volume, current_volume)
# Move the pointer associated with the shorter line inwards.
# This is because moving the taller line will not increase height and will decrease width.
if height_values[left_pointer] < height_values[right_pointer]:
left_pointer += 1
else:
right_pointer -= 1
return maximum_water_volumeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input array is null or empty | A null or empty input array should result in an area of 0. |
| Input array has only one element | An array with a single element cannot form a container, so the maximum area is 0. |
| All heights are the same | The algorithm will correctly find the maximum area as the width decreases and height remains constant. |
| Heights are in strictly increasing or decreasing order | The two-pointer approach efficiently handles these ordered inputs by always moving the pointer of the shorter line. |
| Input array contains zeros | Zeros represent lines with no height, which will correctly contribute 0 to the area calculation. |
| Input array contains very large heights | Ensure the data type used for area calculation can accommodate potential large integer overflows. |
| The maximum area is formed by the outermost lines | The two-pointer approach initialized at the ends naturally checks this scenario first. |
| The maximum area is formed by two lines close to each other with large heights | The iterative shrinking of the container's width allows the algorithm to explore all pairs. |