Container With Most Water #4 Most Asked
MediumYou are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example 1:
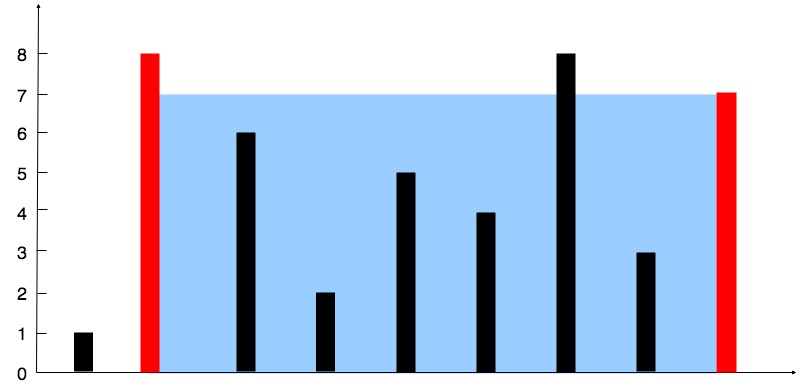
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1] Output: 1
Constraints:
n == height.length2 <= n <= 1050 <= height[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the `height` array? What is the range of values for the elements in the `height` array?
- Can the `height` array contain non-positive values (zeros or negative numbers)?
- If the `height` array is empty or contains only one element, what should the function return?
- If there are multiple pairs of lines that result in the same maximum water capacity, is it acceptable to return any one of those pairs, or is there a specific tie-breaking condition?
- Does the problem statement guarantee that the input array will always be valid (e.g., not null)?
Brute Force Solution
Approach
The problem asks us to find the largest container that can be formed by selecting two vertical lines from a given set of lines. The brute force method involves checking every single possible pair of lines to see which combination forms the largest container. We calculate the area for each pair and keep track of the biggest one we find.
Here's how the algorithm would work step-by-step:
- Pick the first line in the set.
- Now, consider every other line in the set, one at a time, and pair it with the first line.
- For each of these pairs, calculate the area of the container they would form. The width is the distance between the lines, and the height is determined by the shorter of the two lines.
- Remember the largest area you've seen so far.
- Move on to the second line in the original set.
- Again, pair this line with every other line in the set (except for itself, of course).
- Calculate the area for each of these new pairs, and compare it to the largest area you've seen so far, updating the largest area if necessary.
- Continue this process, considering each line in the set as the 'first' line, and pairing it with all other lines.
- After you've gone through all possible pairs of lines, the largest area you remembered is the answer.
Code Implementation
def max_area_brute_force(heights):
max_area = 0
# Iterate through each line as the potential left boundary.
for left_index in range(len(heights)):
# Compare the left boundary with all other lines to find the max area
for right_index in range(left_index + 1, len(heights)):
# Determine the height of the container formed.
current_height = min(heights[left_index], heights[right_index])
#Calculate area using width and bounded height.
current_width = right_index - left_index
area = current_height * current_width
#Update maximum if larger area is found.
max_area = max(max_area, area)
return max_areaBig(O) Analysis
Optimal Solution
Approach
The goal is to find two vertical lines that, along with the bottom axis, will hold the most water. Instead of checking every possible pair of lines, we cleverly narrow down our choices by moving inwards from the widest possible container.
Here's how the algorithm would work step-by-step:
- Start with the container formed by the first and last lines in the arrangement.
- Calculate the amount of water that container can hold.
- Now, compare the heights of the two lines forming this container. If the line on the left is shorter, move the left line inward by one. Otherwise, move the right line inward by one.
- The logic here is that the shorter line is what limits the amount of water held. Moving the shorter line gives us the opportunity to find a taller line that might increase the water held.
- Calculate the water held by this new container.
- Keep moving the shorter line inward and calculating the contained water until the two lines meet.
- The container with the most water found during this process is the solution.
Code Implementation
def max_area(heights):
max_water = 0
left_index = 0
right_index = len(heights) - 1
while left_index < right_index:
# Calculate current container's area
current_width = right_index - left_index
current_height = min(heights[left_index], heights[right_index])
current_water = current_width * current_height
max_water = max(max_water, current_water)
# Move pointer of the shorter line inward
if heights[left_index] < heights[right_index]:
left_index += 1
# Shorter line limits water, move to find a taller line
else:
right_index -= 1
# Shorter line limits water, move to find a taller line
return max_waterBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty or null height array | Return 0 immediately since no container can be formed. |
| Height array with only one element | Return 0 since a container needs at least two lines. |
| Height array with only two elements | Calculate the area formed by these two lines and return it. |
| Height array with all elements equal to 0 | The algorithm should return 0 as the container can hold no water. |
| Height array with very large values that could cause integer overflow when calculating area | Use long to store the area to prevent potential overflow. |
| Height array where all elements are in descending order | The algorithm correctly explores container areas even when heights are non-increasing. |
| Height array where all elements are in ascending order | The algorithm correctly explores container areas even when heights are non-decreasing. |
| Height array contains duplicate heights | The algorithm handles duplicate heights correctly as it considers all possible pairs. |