Count Good Nodes in Binary Tree
MediumGiven a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.
Return the number of good nodes in the binary tree.
Example 1:
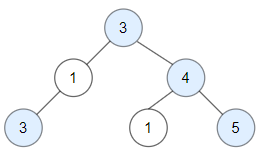
Input: root = [3,1,4,3,null,1,5] Output: 4 Explanation: Nodes in blue are good. Root Node (3) is always a good node. Node 4 -> (3,4) is the maximum value in the path starting from the root. Node 5 -> (3,4,5) is the maximum value in the path Node 3 -> (3,1,3) is the maximum value in the path.
Example 2:

Input: root = [3,3,null,4,2] Output: 3 Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
Example 3:
Input: root = [1] Output: 1 Explanation: Root is considered as good.
Constraints:
- The number of nodes in the binary tree is in the range
[1, 10^5]. - Each node's value is between
[-10^4, 10^4].
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree? Are negative values possible?
- Can the tree be empty (root is null)? If so, what should I return?
- By 'path from the root to that node,' do you mean the unique path of parent-child relationships?
- If a node's value is equal to the maximum value along the path from the root, is it still considered a 'good' node?
- Are we concerned about potential stack overflow issues with very deep trees?
Brute Force Solution
Approach
The brute force approach to counting 'good' nodes in a binary tree involves looking at each node and comparing its value to all nodes on the path from the root to that node. We call a node 'good' if it's greater than or equal to all nodes on this path. We need to repeat this process for every single node in the entire tree.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, which is the root.
- Look at the current node, and trace back the path from this node all the way to the root of the tree. This gives you a sequence of nodes.
- Compare the current node's value to the values of all the nodes you encountered on that path back to the root.
- If the current node's value is greater than or equal to every single node on the path to the root, then mark this node as a 'good' node.
- Now, go to the left child of the current node, and repeat the process starting from step two.
- After checking the left child, go to the right child of the current node, and repeat the process starting from step two.
- Continue doing this, checking every single node in the entire tree, until you have looked at all the nodes.
- Finally, count up how many 'good' nodes you have found and that is your answer.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def count_good_nodes_brute_force(root):
number_of_good_nodes = 0
def is_good_node(node, path_to_root):
# Check if the current node's value is greater than or equal to every node on the path.
for parent_node_value in path_to_root:
if node.val < parent_node_value:
return False
return True
def traverse_tree(node, path_to_root):
nonlocal number_of_good_nodes
if not node:
return
# Check if the current node is a 'good' node.
if is_good_node(node, path_to_root):
number_of_good_nodes += 1
# Add the current node's value to the path before traversing its children.
new_path_to_root = path_to_root + [node.val]
# Traverse the left subtree.
traverse_tree(node.left, new_path_to_root)
# Traverse the right subtree.
traverse_tree(node.right, new_path_to_root)
traverse_tree(root, [])
return number_of_good_nodesBig(O) Analysis
Optimal Solution
Approach
The problem asks us to find how many nodes in a binary tree are considered 'good'. A node is 'good' if all nodes on the path from the root to that node have a value less than or equal to the current node's value. The optimal approach is a depth-first search (DFS) where we keep track of the maximum value seen so far on the path from the root.
Here's how the algorithm would work step-by-step:
- Start at the root of the tree and consider it as the current node.
- Keep track of the largest value you've encountered so far as you move down the tree; start this value at negative infinity.
- Check if the current node's value is greater than or equal to the largest value encountered so far. If it is, increment a counter (this node is 'good') and update the largest value seen so far to be the current node's value.
- Move to the left child of the current node and repeat the process, passing along the largest value seen so far. If there is no left child, skip this step.
- Move to the right child of the current node and repeat the process, again passing along the largest value seen so far. If there is no right child, skip this step.
- Continue this process until you have visited all nodes in the tree. The final count will represent the number of 'good' nodes.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def goodNodes(root: TreeNode) -> int:
def depthFirstSearch(node: TreeNode, maximum_value_so_far: int) -> int:
if not node:
return 0
good_node_count = 0
# Check if the current node is a 'good' node.
if node.val >= maximum_value_so_far:
good_node_count = 1
#Update max seen so far, because current node is good
maximum_value_so_far = node.val
# Traverse left subtree.
good_node_count += depthFirstSearch(node.left, maximum_value_so_far)
# Traverse right subtree.
good_node_count += depthFirstSearch(node.right, maximum_value_so_far)
return good_node_count
# Initialize DFS with negative infinity
return depthFirstSearch(root, float('-inf'))Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return 0 immediately because there are no nodes. |
| Single node tree | Return 1 because the root node is always a good node in this case. |
| Tree with all nodes having the same value | Every node will be a good node, so the count will equal the number of nodes in the tree, handled by the recursive condition. |
| Tree where values strictly decrease from root to leaves | Only the root node will be good, so the result will be 1 and this case is already covered by recursive checks. |
| Tree where values strictly increase from root to leaves | All nodes will be good nodes, increment count at each recursive step and it will handle this. |
| Tree with negative node values | The algorithm should handle negative values correctly as it relies on numerical comparisons, it will function as normal. |
| Skewed tree (all nodes on one side) | The recursion depth could be large, but should still be within reasonable limits for most test cases, handled by the recursion stack, not a major concern. |
| Integer overflow with large tree depth and node values | While node values are usually bounded, be mindful of potential overflow with very deep trees and large int values, which requires using a larger data type such as long if needed or handle overflow if necessary. |