Count Lattice Points Inside a Circle
MediumGiven a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return the number of lattice points that are present inside at least one circle.
Note:
- A lattice point is a point with integer coordinates.
- Points that lie on the circumference of a circle are also considered to be inside it.
Example 1:
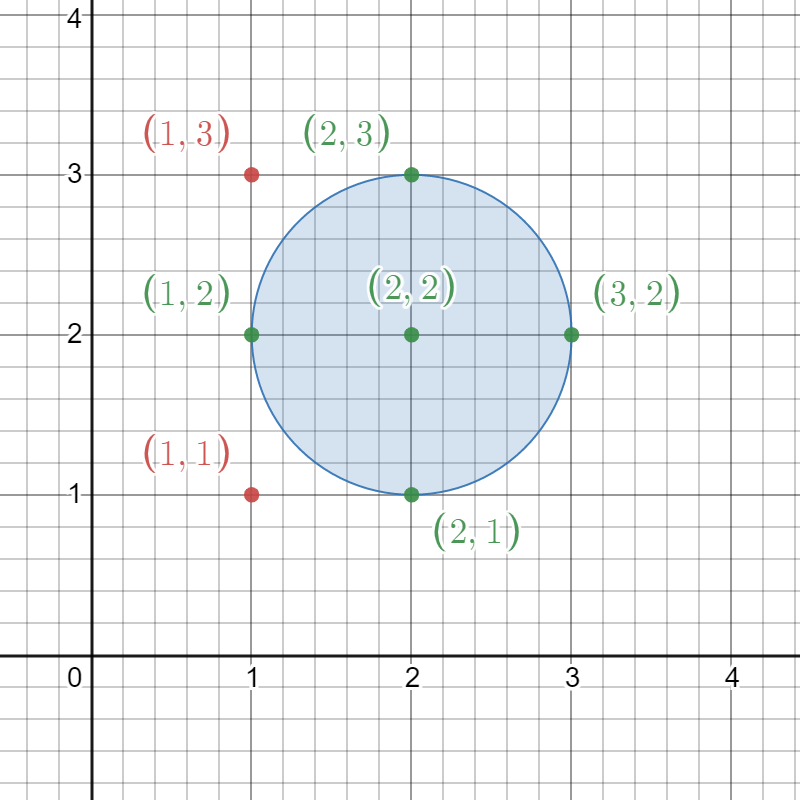
Input: circles = [[2,2,1]] Output: 5 Explanation: The figure above shows the given circle. The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green. Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle. Hence, the number of lattice points present inside at least one circle is 5.
Example 2:
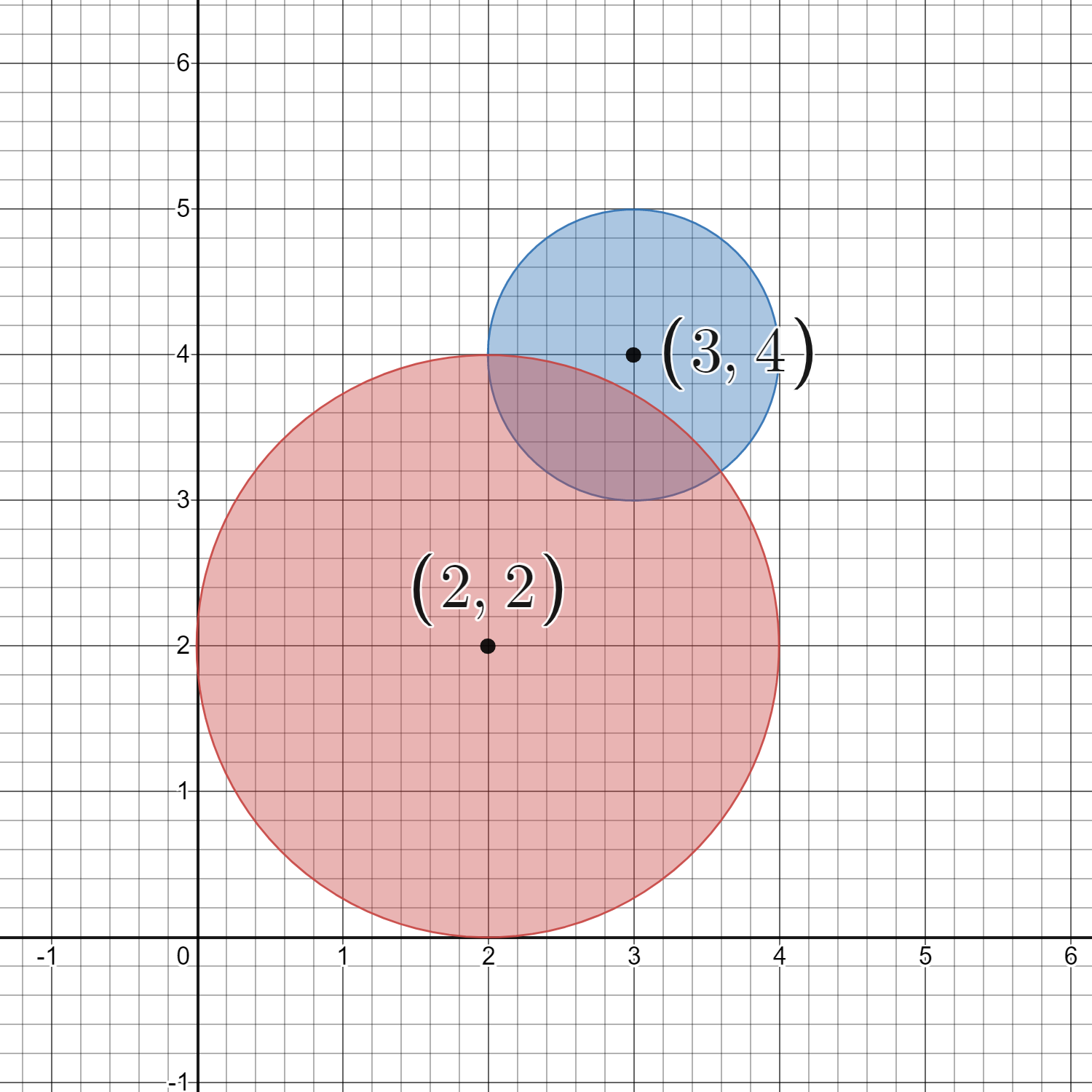
Input: circles = [[2,2,2],[3,4,1]] Output: 16 Explanation: The figure above shows the given circles. There are exactly 16 lattice points which are present inside at least one circle. Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).
Constraints:
1 <= circles.length <= 200circles[i].length == 31 <= xi, yi <= 1001 <= ri <= min(xi, yi)
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the values of xi, yi, and ri? What are the maximum and minimum possible values, and are they integers?
- What is the maximum number of circles I should expect in the input array?
- Can the radii of the circles be zero? If so, what should I do with a circle of radius zero?
- Is there any overlap between the circles? Should I handle overlapping regions to ensure I count each lattice point only once?
- Do I need to worry about integer overflow when calculating the distance between a lattice point and the center of a circle?
Brute Force Solution
Approach
The brute force approach here is like checking every single point on a grid to see if it's inside the circle. We systematically go through each potential point and test it.
Here's how the algorithm would work step-by-step:
- Imagine a large square that completely surrounds the circle.
- Start at the bottom-left corner of the square and move to the right, one point at a time.
- For each point, calculate the distance between that point and the center of the circle.
- If the distance is less than or equal to the circle's radius, then that point is inside (or on) the circle, so count it.
- Continue moving to the right until you reach the edge of the square, then move up one row and start again from the left edge of the square.
- Repeat this process until you have checked every point within the entire square.
- The total number of points you counted is the answer.
Code Implementation
def count_lattice_points_inside_circle(radius):
circle_center_x = 0
circle_center_y = 0
count = 0
# Define the bounds of the square containing the circle
square_side_length = 2 * radius
# Iterate through all possible lattice points within the square.
for x_coordinate in range(-radius, radius + 1):
for y_coordinate in range(-radius, radius + 1):
# Calculate the distance between the point and the center.
distance_from_center = (
(x_coordinate - circle_center_x) ** 2 +
(y_coordinate - circle_center_y) ** 2
) ** 0.5
# Check if the point is inside or on the circle's boundary.
if distance_from_center <= radius:
# Count the point if it is inside the circle.
count += 1
return count
Big(O) Analysis
Optimal Solution
Approach
Instead of checking every single point to see if it's inside the circle, the optimal approach efficiently searches only the points that could possibly be inside. It leverages the circle's boundaries to reduce the number of points we need to check, significantly speeding up the process.
Here's how the algorithm would work step-by-step:
- Find the smallest and largest possible x and y coordinates of points that could be inside or on the edge of the circle. Think of this as drawing a square around the circle and only focusing on points inside the square.
- For each possible x-coordinate within the range, determine the possible y-coordinates that would keep the point within the circle. You can do this by using the circle's equation to figure out the upper and lower bounds for y.
- Count each of the valid x,y points that you found that fall within the circle, and add them to your total count. You only want to count unique lattice points.
- Return the total number of unique lattice points that were found inside the circle.
Code Implementation
def count_lattice_points(circles):
unique_points = set()
for circle_x, circle_y, radius in circles:
min_x = circle_x - radius
max_x = circle_x + radius
min_y = circle_y - radius
max_y = circle_y + radius
# Iterate through possible x values within the circle's bounding box
for x_coordinate in range(min_x, max_x + 1):
# Iterate through possible y values within the circle's bounding box
for y_coordinate in range(min_y, max_y + 1):
# Check if the point (x, y) is inside the circle
if (x_coordinate - circle_x)**2 + (y_coordinate - circle_y)**2 <= radius**2:
# Add the point to the set of unique points
unique_points.add((x_coordinate, y_coordinate))
# The total number of unique lattice points inside all circles
return len(unique_points)
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty circles array | Return 0 since no circles exist, thus no lattice points can be inside. |
| Circles with radius 0 | Only the center point should be counted for these circles. |
| Circles with very large radius, causing potential integer overflow when calculating distances (x-xi)^2 + (y-yi)^2 | Use long or double to store the intermediate results to prevent overflow. |
| Circles with negative coordinates for the center | The solution should correctly handle negative coordinates as valid positions on the plane. |
| Circles that are far apart from each other, requiring a large iteration space | Optimize iteration space by considering a bounding box around all circles to limit the search space. |
| Circles that are heavily overlapping | Use a set to store unique lattice points to avoid double-counting overlapping regions. |
| Circles with extremely large or small coordinates, potentially leading to performance issues or floating-point inaccuracies | Scale or normalize coordinates if necessary, and use appropriate data types with sufficient precision. |
| Maximum number of circles specified by the problem constraints | Ensure the solution's time and space complexity remain within acceptable bounds for the maximum input size. |