Count Number of Rectangles Containing Each Point
MediumYou are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).
The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).
Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jth point.
The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.
Example 1:
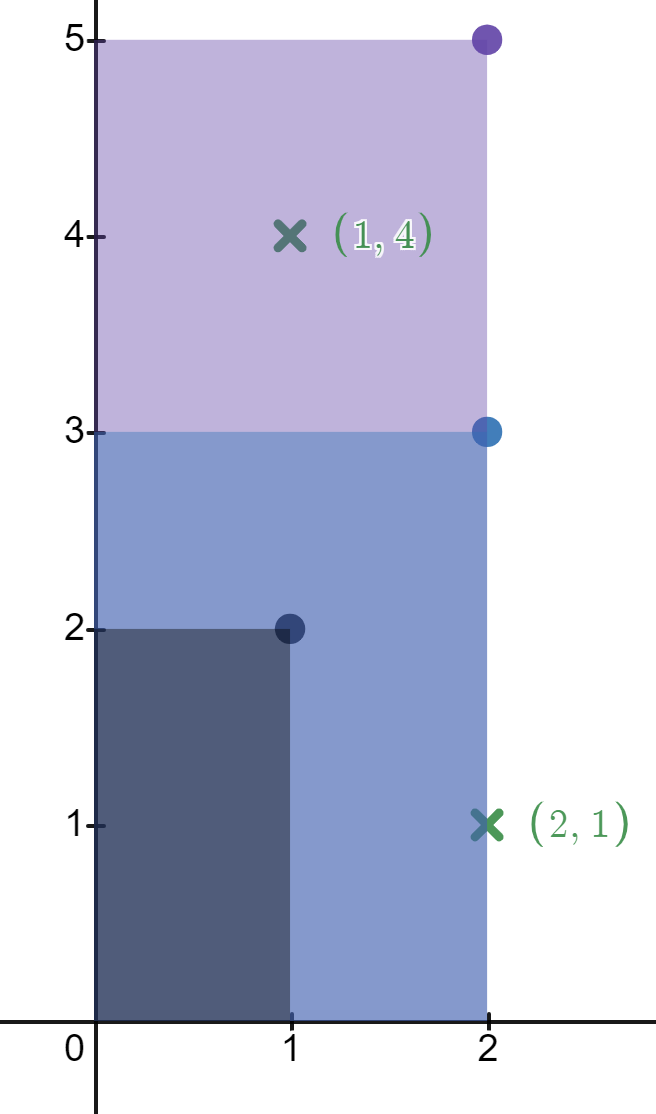
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]] Output: [2,1] Explanation: The first rectangle contains no points. The second rectangle contains only the point (2, 1). The third rectangle contains the points (2, 1) and (1, 4). The number of rectangles that contain the point (2, 1) is 2. The number of rectangles that contain the point (1, 4) is 1. Therefore, we return [2, 1].
Example 2:

Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]] Output: [1,3] Explanation: The first rectangle contains only the point (1, 1). The second rectangle contains only the point (1, 1). The third rectangle contains the points (1, 3) and (1, 1). The number of rectangles that contain the point (1, 3) is 1. The number of rectangles that contain the point (1, 1) is 3. Therefore, we return [1, 3].
Constraints:
1 <= rectangles.length, points.length <= 5 * 104rectangles[i].length == points[j].length == 21 <= li, xj <= 1091 <= hi, yj <= 100- All the
rectanglesare unique. - All the
pointsare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the maximum values for the x and y coordinates of the rectangles and points, and what is the maximum number of rectangles and points?
- Can the coordinates of the rectangles and points be floating-point numbers, or are they always integers?
- If a point lies exactly on the border of a rectangle (or on a corner), should it be considered as 'contained' within that rectangle?
- Can the input arrays (rectangles and points) be empty or null?
- Is the order of the output array (the count of containing rectangles for each point) expected to match the order of points in the input array points?
Brute Force Solution
Approach
The brute force approach for this rectangle problem is to check every rectangle against every point. We'll go through each point one by one, and for each point, we'll count how many rectangles contain it.
Here's how the algorithm would work step-by-step:
- Take the first point we need to check.
- Now, look at the first rectangle.
- Check if that rectangle contains the point.
- If it does, increase our count.
- If not, move on.
- Repeat this process (checking if the rectangle contains the point and updating the count) for every rectangle we have.
- Once we've checked all the rectangles, we know how many rectangles contain that first point. Write down that number.
- Now, move to the next point and repeat the entire process (checking against all rectangles and counting).
- Continue this until we have counted the number of rectangles containing each point.
Code Implementation
def count_rectangles_containing_each_point(rectangles, points):
number_of_rectangles_containing_point = []
for point_index in range(len(points)):
point = points[point_index]
count = 0
# Iterate through each rectangle to check if it contains the current point
for rectangle_index in range(len(rectangles)):
rectangle = rectangles[rectangle_index]
# Check if the point is within the bounds of the rectangle
if rectangle[0] <= point[0] and rectangle[1] <= point[1]:
count += 1
number_of_rectangles_containing_point.append(count)
return number_of_rectangles_containing_pointBig(O) Analysis
Optimal Solution
Approach
The efficient strategy involves sorting the rectangles to help us quickly find the ones that could possibly contain a given point. Then, for each point, we efficiently count how many rectangles actually do contain it, using the sorted information to skip unnecessary checks.
Here's how the algorithm would work step-by-step:
- First, organize the rectangles based on their heights from tallest to shortest. This will help us later.
- Then, for each point we want to check, use a method that helps us to quickly find the rectangles whose heights are tall enough to possibly contain the point. Because we sorted the rectangles, we can quickly find the 'cutoff' point in our sorted list of rectangle heights.
- From this subset of rectangles, only check the rectangles that are as wide or wider than the point's horizontal position. If a rectangle is wide and tall enough, it must contain the point, so we add it to our count.
- Continue this process for each point, and the result will be a list of the number of rectangles that contain each respective point.
Code Implementation
def count_rectangles(rectangles, points):
rectangle_counts = []
# Sort rectangles by height in descending order.
rectangles.sort(key=lambda x: x[1], reverse=True)
for point_x, point_y in points:
count = 0
# Iterate through sorted rectangles.
for rectangle_x, rectangle_y in rectangles:
# Skip rectangles that are too short.
if rectangle_y < point_y:
break
# Only count rectangles that contain the point.
if rectangle_x >= point_x:
count += 1
rectangle_counts.append(count)
return rectangle_countsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| rectangles array is null or empty | Return an empty array of counts immediately, as there are no rectangles to consider. |
| points array is null or empty | Return an empty array of counts immediately, as there are no points to check. |
| rectangles array contains rectangles with zero area (e.g., height or width is zero) | These rectangles should not contribute to the count and the solution should ignore them or handle them gracefully, potentially by skipping them in the area calculation. |
| points array contains points with very large coordinates (close to integer limits) | Ensure calculations (e.g., comparing coordinates) don't cause integer overflow by using appropriate data types (e.g., long). |
| rectangles array contains rectangles with negative coordinates | The problem statement typically assumes non-negative coordinates; clarify the expected behavior (either reject negative coordinates or interpret them correctly based on the desired coordinate system). |
| All points lie outside all rectangles | The expected output array will contain all zeros; the algorithm should correctly handle this scenario without errors. |
| All points lie inside all rectangles | The expected output array will contain the total number of rectangles for each point; the algorithm should compute this correctly. |
| The number of rectangles and points is very large (close to the maximum constraints) | Consider the time and space complexity; an O(n*m) solution (n rectangles, m points) might be too slow; optimize by sorting or using spatial indexing if necessary. |