Count Sub Islands #20 Most Asked
MediumYou are given two m x n binary matrices grid1 and grid2 containing only 0's (representing water) and 1's (representing land). An island is a group of 1's connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.
An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2.
Return the number of islands in grid2 that are considered sub-islands.
Example 1:
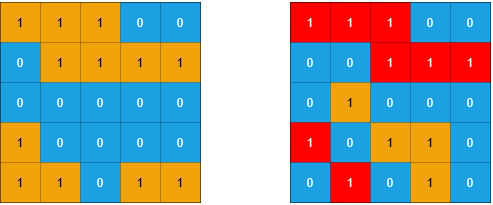
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]] Output: 3 Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2. The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.
Example 2:
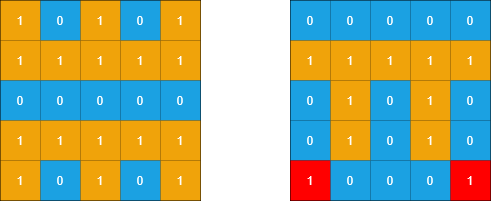
Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]] Output: 2 Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2. The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.
Constraints:
m == grid1.length == grid2.lengthn == grid1[i].length == grid2[i].length1 <= m, n <= 500grid1[i][j]andgrid2[i][j]are either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the two input grids, and what is the maximum size of the grids?
- Can the values in the grid only be 0 or 1, or are other values possible?
- What should I return if either or both of the grids are null or empty?
- Is a sub-island defined as a connected component of 1s in grid2 that is entirely surrounded by 0s or the boundary of grid2, and also completely contained within a connected component of 1s in grid1?
- Are the grids guaranteed to be rectangular (i.e., all rows have the same length)?
Brute Force Solution
Approach
The brute force way to find sub islands is to check every possible piece of the first map and see if it's completely contained within the second map. We'll essentially check every matching land area in the first map to see if it represents a 'sub island'.
Here's how the algorithm would work step-by-step:
- Look at each land area of the first map, one at a time.
- For each land area, check if it also exists on the second map.
- If the land exists on both maps, trace its boundaries on the first map.
- Then, verify that all the land connected to that first piece on the first map also exists and is connected on the second map.
- If any part of the connected land from the first map is missing on the second map, that piece is not a sub-island, so discard it.
- If the entire connected land from the first map is found within the second map, then it is considered a sub-island, so count it.
- Repeat this process for every single land area in the first map to find all the sub-islands.
Code Implementation
def count_sub_islands_brute_force(grid1, grid2):
rows = len(grid1)
cols = len(grid1[0])
sub_island_count = 0
def is_valid(row, col):
return 0 <= row < rows and 0 <= col < cols
def explore_island(row, col, visited, grid):
if not is_valid(row, col) or grid[row][col] == 0 or (row, col) in visited:
return
visited.add((row, col))
explore_island(row + 1, col, visited, grid)
explore_island(row - 1, col, visited, grid)
explore_island(row, col + 1, visited, grid)
explore_island(row, col - 1, visited, grid)
def get_island_coordinates(row, col, grid):
island_coordinates = set()
visited = set()
explore_island(row, col, visited, grid)
return visited
for row in range(rows):
for col in range(cols):
if grid1[row][col] == 1:
# Check if land exists in both grids
if grid2[row][col] == 1:
island1_coordinates = get_island_coordinates(row, col, grid1)
is_sub_island = True
for island_row, island_col in island1_coordinates:
# Ensure that all land in grid1 exists in grid2
if not (is_valid(island_row, island_col) and grid2[island_row][island_col] == 1):
is_sub_island = False
break
if is_sub_island:
sub_island_count += 1
return sub_island_countBig(O) Analysis
Optimal Solution
Approach
The goal is to identify 'islands' in a smaller map that are completely contained within 'islands' of a larger map. We can efficiently determine this by eliminating 'islands' on the smaller map that touch the edges or overlap with water on the larger map, and then counting the remaining 'islands'.
Here's how the algorithm would work step-by-step:
- First, examine the edges of the smaller map. If any land cells on the edge are part of an 'island', those entire 'islands' cannot be sub-islands because they're not fully contained.
- Mark these 'islands' as 'not sub-islands' by changing the land to water, effectively eliminating them.
- Next, compare the smaller map to the larger map. For every land cell on the smaller map, check if the corresponding cell on the larger map is also land. If it's water on the larger map, then the 'island' on the smaller map cannot be a sub-island.
- Again, mark these invalid 'islands' as water on the smaller map.
- Finally, count the number of remaining 'islands' on the modified smaller map. Each of these represents a sub-island completely contained within an 'island' of the larger map.
Code Implementation
def count_sub_islands(grid_one, grid_two):
rows = len(grid_one)
cols = len(grid_one[0])
def sink_island(row, col, grid):
if row < 0 or row >= rows or col < 0 or col >= cols or grid[row][col] == 0:
return
grid[row][col] = 0
sink_island(row + 1, col, grid)
sink_island(row - 1, col, grid)
sink_island(row, col + 1, grid)
sink_island(row, col - 1, grid)
# Eliminate islands on the border of grid_two
for row in range(rows):
sink_island(row, 0, grid_two)
sink_island(row, cols - 1, grid_two)
for col in range(cols):
sink_island(0, col, grid_two)
sink_island(rows - 1, col, grid_two)
# Eliminate islands in grid_two where grid_one is water
for row in range(rows):
for col in range(cols):
# Sink islands in grid_two if corresponding cell in grid_one is water
if grid_one[row][col] == 0 and grid_two[row][col] == 1:
sink_island(row, col, grid_two)
sub_islands_count = 0
# Count remaining islands in grid_two
for row in range(rows):
for col in range(cols):
if grid_two[row][col] == 1:
# Increment the count as each island represents a sub-island
sub_islands_count += 1
sink_island(row, col, grid_two)
return sub_islands_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| grid1 or grid2 is null or empty | Return 0 if either grid is null or has zero rows or columns as there can be no subislands. |
| grids have different dimensions | Return 0 if the grids have different dimensions, indicating grid2 cannot be a subisland of grid1. |
| grid2 is entirely 0s | Return 0, as there are no islands in grid2 to be subislands of grid1. |
| grid2 is entirely 1s, but grid1 is not entirely 1s | Iterate through grid2 and mark as not subisland any cell that is 1 and the corresponding cell in grid1 is 0. |
| grid1 and grid2 are identical and all 1s | Return 1 since grid2 is an island and is a subisland of itself in grid1. |
| A very large grid to test for stack overflow during DFS/BFS | Use iterative BFS instead of recursive DFS to prevent potential stack overflow errors. |
| Grid contains only one island in grid2 | The algorithm should correctly identify this single island as a subisland if it exists in grid1. |
| An island in grid2 touches the boundary of the grid but isn't present in grid1 | The boundary check in the island identification step will prevent this invalid subisland from being counted. |