Cousins in Binary Tree
EasyGiven the root of a binary tree with unique values and the values of two different nodes of the tree x and y, return true if the nodes corresponding to the values x and y in the tree are cousins, or false otherwise.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Note that in a binary tree, the root node is at the depth 0, and children of each depth k node are at the depth k + 1.
Example 1:
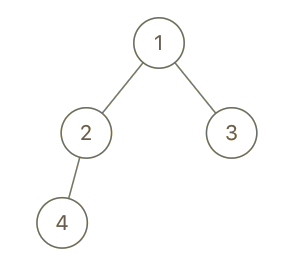
Input: root = [1,2,3,4], x = 4, y = 3 Output: false
Example 2:
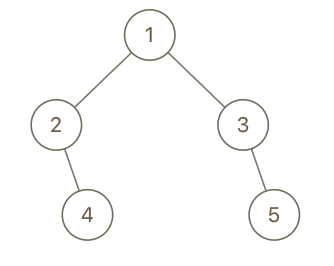
Input: root = [1,2,3,null,4,null,5], x = 5, y = 4 Output: true
Example 3:

Input: root = [1,2,3,null,4], x = 2, y = 3 Output: false
Constraints:
- The number of nodes in the tree is in the range
[2, 100]. 1 <= Node.val <= 100- Each node has a unique value.
x != yxandyare exist in the tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary tree be empty, and if so, what should I return?
- Are the values of the nodes guaranteed to be unique across the tree, or can there be duplicate node values?
- Are the values 'x' and 'y' guaranteed to exist in the tree, and if not, what should I return?
- If 'x' and 'y' are the same value but at different depths, are they considered cousins, or should I only compare nodes with differing values?
- By 'cousins', do you mean they must have the same depth in the tree AND have different parents?
Brute Force Solution
Approach
To find if two tree nodes are cousins using brute force, we explore the entire tree to gather information about each node's depth and parent. Then, we simply compare the gathered information to determine if the two nodes meet the criteria for being cousins.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree.
- Explore every single branch of the tree, one by one, going all the way down to the leaves.
- While exploring, for each node we encounter, remember how far away from the top of the tree it is (its depth).
- Also, for each node, remember who its parent is - the node directly above it.
- Once you've looked at every single node in the tree, find the two specific nodes we're interested in.
- Check if they are at the same depth in the tree. If not, they can't be cousins, so we're done.
- If they are at the same depth, check if they have different parents. If they do, then they are cousins.
- If they have the same parent, they are siblings, not cousins.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def cousins_in_binary_tree(root, node_a, node_b):
if root is None or node_a is None or node_b is None:
return False
node_a_depth = -1
node_b_depth = -1
node_a_parent = None
node_b_parent = None
def dfs(node, depth, parent):
nonlocal node_a_depth, node_b_depth, node_a_parent, node_b_parent
if node is None:
return
if node == node_a:
node_a_depth = depth
node_a_parent = parent
if node == node_b:
node_b_depth = depth
node_b_parent = parent
dfs(node.left, depth + 1, node)
# Explore the right subtree.
dfs(node.right, depth + 1, node)
dfs(root, 0, None)
# Nodes must be at the same depth to be cousins.
if node_a_depth != node_b_depth:
return False
# Nodes must have different parents to be cousins.
if node_a_parent == node_b_parent:
return False
return TrueBig(O) Analysis
Optimal Solution
Approach
To determine if two nodes are cousins in a binary tree, we need to find their parents and depths. The optimal approach involves exploring the tree once to record this information, and then comparing it for the two nodes in question.
Here's how the algorithm would work step-by-step:
- Begin by examining the root of the tree.
- As you explore the tree, keep track of the depth of each node (its distance from the root).
- Also, remember the parent of each node as you go down the tree.
- Once you have found both target nodes, check if their depths are the same.
- Next, verify that their parents are different.
- If the nodes have the same depth but different parents, they are cousins.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def are_cousins(root, node_one, node_two):
if root is None:
return False
node_one_parent = None
node_two_parent = None
node_one_depth = -1
node_two_depth = -1
def dfs(node, parent, depth):
nonlocal node_one_parent, node_two_parent, node_one_depth, node_two_depth
if node is None:
return
if node.value == node_one.value:
node_one_parent = parent
node_one_depth = depth
if node.value == node_two.value:
node_two_parent = parent
node_two_depth = depth
# Optimization: if both nodes are found, no need to traverse further.
if node_one_parent and node_two_parent:
return
dfs(node.left, node, depth + 1)
dfs(node.right, node, depth + 1)
dfs(root, None, 0)
# Must have the same depth and differing parents to be cousins.
if node_one_depth == node_two_depth:
# Prevents nodes from being siblings.
if node_one_parent != node_two_parent:
return True
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return false immediately as there are no nodes to be cousins. |
| Tree with only one node | Return false since x and y cannot both exist in a single-node tree. |
| x or y not present in the tree | Return false as x and y must both exist to be cousins. |
| x and y are the same node | Return false since cousin definition implies distinct nodes. |
| x and y are siblings (same parent) | Return false because siblings are not cousins. |
| Large tree with skewed distribution and x, y deep in the tree | BFS/DFS should still correctly identify cousins, but consider optimizing for space complexity if memory becomes a bottleneck, possibly using iterative DFS with explicit stack management. |
| Integer overflow when calculating depth (if using recursive approach without careful checking) | Use a data type with a larger range, or implement iterative depth calculation to avoid stack overflow and depth related errors. |
| x and y have the same value but are different nodes | Node comparison must be based on node object identity, not just value equality, to distinguish them. |