Cut Off Trees for Golf Event
HardYou are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:
0means the cell cannot be walked through.1represents an empty cell that can be walked through.- A number greater than
1represents a tree in a cell that can be walked through, and this number is the tree's height.
In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.
You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).
Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.
Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.
Example 1:
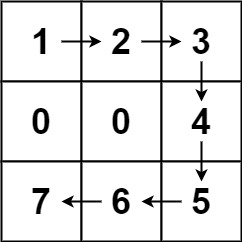
Input: forest = [[1,2,3],[0,0,4],[7,6,5]] Output: 6 Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.
Example 2:
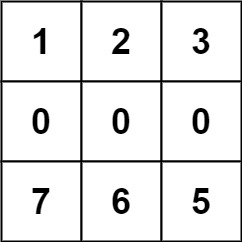
Input: forest = [[1,2,3],[0,0,0],[7,6,5]] Output: -1 Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.
Example 3:
Input: forest = [[2,3,4],[0,0,5],[8,7,6]] Output: 6 Explanation: You can follow the same path as Example 1 to cut off all the trees. Note that you can cut off the first tree at (0, 0) before making any steps.
Constraints:
m == forest.lengthn == forest[i].length1 <= m, n <= 500 <= forest[i][j] <= 109- Heights of all trees are distinct.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the forest (number of rows and columns)?
- Can the tree heights be zero, negative, or non-integer?
- If it's impossible to cut all the trees in ascending order of height, what value should I return?
- If there are multiple paths to a tree with the same height, should I take the shortest path?
- Is the starting point (0, 0) always guaranteed to be traversable (height > 0)?
Brute Force Solution
Approach
The brute force approach in this problem involves trying every single path to cut down all the trees. We'll explore all possible orders of visiting the trees and calculate the total distance for each order.
Here's how the algorithm would work step-by-step:
- First, find all the trees you need to cut down and list them based on their height from shortest to tallest.
- Start with the first tree's location.
- Consider every possible next tree to visit from the current tree. Calculate the distance to each of these trees.
- Choose one of the possible next trees and move to that location. Remember which trees you have already visited and the total distance you have traveled so far.
- Repeat the previous step by considering the remaining unvisited trees from your new location, always calculating the distance and adding it to your total.
- Continue this process until you have visited all the trees.
- Record the total distance it took to visit all the trees in this specific order.
- Now, go back to the start and try a different order of visiting the trees. Repeat steps 3-7.
- Do this for every single possible order of visiting the trees.
- Finally, compare all the recorded total distances. The smallest distance represents the best path to cut down all the trees.
Code Implementation
def cut_off_trees_for_golf_event_brute_force(forest):
number_of_rows = len(forest)
number_of_columns = len(forest[0])
trees_to_cut = []
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
tree_height = forest[row_index][column_index]
if tree_height > 1:
trees_to_cut.append((tree_height, row_index, column_index))
trees_to_cut.sort()
def calculate_manhattan_distance(start_row, start_column, end_row, end_column):
return abs(start_row - end_row) + abs(start_column - end_column)
import itertools
shortest_distance = float('inf')
# Try all permutations of tree cutting orders.
for permutation in itertools.permutations(trees_to_cut):
current_row = 0
current_column = 0
total_distance_for_permutation = 0
# Sum up distance between each tree.
for tree_height, next_row, next_column in permutation:
distance = calculate_manhattan_distance(current_row, current_column, next_row, next_column)
total_distance_for_permutation += distance
current_row = next_row
current_column = next_column
# Keep track of the smallest total distance seen
shortest_distance = min(shortest_distance, total_distance_for_permutation)
if shortest_distance == float('inf'):
return -1
else:
return shortest_distanceBig(O) Analysis
Optimal Solution
Approach
The key to efficiently cutting trees for the golf event is to visit them in increasing order of height, as smaller trees should always be cut before taller ones. We use a shortest path finding algorithm, like navigating a maze, to move from one tree to the next, always aiming for the closest uncut tree.
Here's how the algorithm would work step-by-step:
- First, get a list of all the trees that need to be cut down, and sort them from smallest to largest based on their height.
- Start at the beginning point (the origin).
- Find the shortest path (the fewest steps) from where you are now to the next tree in the sorted list.
- If you can't reach the next tree (there's no path), it's impossible to cut all trees, so the task is impossible.
- If you can reach the tree, add the number of steps it took to get there to a running total of steps taken.
- Once you've reached the tree, cut it down (mark that spot as traversable).
- Make the location of the tree that you reached your new starting point.
- Repeat the process until you've cut down all the trees in the list.
- The total number of steps you've taken is the answer.
Code Implementation
from collections import deque
def cut_off_trees(forest):
tree_locations = []
rows = len(forest)
cols = len(forest[0])
for row in range(rows):
for col in range(cols):
height = forest[row][col]
if height > 1:
tree_locations.append((height, row, col))
tree_locations.sort()
start_row, start_col = 0, 0
total_steps = 0
for height, target_row, target_col in tree_locations:
steps = find_shortest_path(forest, start_row, start_col, target_row, target_col)
if steps == -1:
return -1
total_steps += steps
start_row, start_col = target_row, target_col
forest[target_row][target_col] = 1
return total_steps
def find_shortest_path(forest, start_row, start_col, target_row, target_col):
rows = len(forest)
cols = len(forest[0])
queue = deque([(start_row, start_col, 0)])
visited = set()
visited.add((start_row, start_col))
# Define possible movement directions: up, down, left, right
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
while queue:
current_row, current_col, steps = queue.popleft()
if current_row == target_row and current_col == target_col:
return steps
for delta_row, delta_col in directions:
new_row = current_row + delta_row
new_col = current_col + delta_col
# Check boundary conditions and if cell is traversable
if 0 <= new_row < rows and 0 <= new_col < cols and \
forest[new_row][new_col] > 0 and (new_row, new_col) not in visited:
queue.append((new_row, new_col, steps + 1))
visited.add((new_row, new_col))
# If no path is found return -1
return -1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty forest input | Return -1 immediately as no path can be calculated. |
| Forest with only one cell | If the single cell has a tree (value > 1), return 0; otherwise, return -1 because all trees must be cut. |
| No trees to cut (all values are 0 or 1) | If no tree exists (value > 1), return 0 if the starting position is already at a tree, else -1. |
| Trees are not in strictly increasing order of height | Sort the trees by height before processing. |
| No path exists between two trees | Return -1 if the BFS search for a specific tree returns no valid path. |
| Large forest dimensions leading to potential memory issues with BFS | Implement BFS using an iterative approach with a queue to avoid stack overflow and optimize memory usage. |
| Integer overflow when calculating distance or accumulated steps | Use long data type for distance calculations to prevent overflow. |
| Forest containing a tree at the starting location (0, 0) | The algorithm should correctly handle starting at a tree and consider it cut. |