Determine Whether Matrix Can Be Obtained By Rotation
EasyGiven two n x n binary matrices mat and target, return true if it is possible to make mat equal to target by rotating mat in 90-degree increments, or false otherwise.
Example 1:
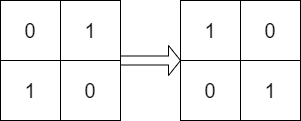
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]] Output: true Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.
Example 2:
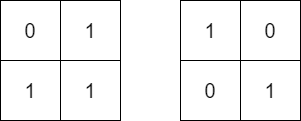
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]] Output: false Explanation: It is impossible to make mat equal to target by rotating mat.
Example 3:
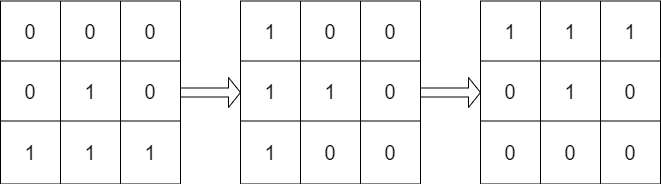
Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]] Output: true Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.
Constraints:
n == mat.length == target.lengthn == mat[i].length == target[i].length1 <= n <= 10mat[i][j]andtarget[i][j]are either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the input matrices `mat` and `target`?
- Are the integer elements in the matrices bounded by a specific range?
- Is it guaranteed that `mat` and `target` will always be square matrices of the same size, or should I handle cases where they are not?
- If none of the rotations of `mat` result in `target`, should I return `false`?
- Are the matrices always non-null?
Brute Force Solution
Approach
The brute force approach involves trying out all possible rotations of the original matrix and comparing each rotated version to the target matrix. We essentially rotate the matrix in place 90 degrees at a time, checking for a match after each rotation. If none of the rotations match, the matrices are not obtainable through rotation.
Here's how the algorithm would work step-by-step:
- First, check if the two matrices are identical as is. If they are, then the target is obtainable.
- Next, rotate the original matrix by 90 degrees clockwise.
- Compare the rotated matrix with the target matrix. If they match, then the target is obtainable.
- If they don't match, rotate the matrix another 90 degrees clockwise (so, a total of 180 degrees from the original).
- Compare this new rotated matrix with the target matrix. If they match, then the target is obtainable.
- If they still don't match, rotate the matrix once more by 90 degrees clockwise (so, a total of 270 degrees from the original).
- Compare this final rotated matrix with the target matrix. If they match, then the target is obtainable.
- If after all these rotations and comparisons, none of the rotated matrices matched the target matrix, then the target is not obtainable by rotating the original matrix.
Code Implementation
def determine_if_matrix_can_be_obtained_by_rotation(matrix, target):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
if matrix == target:
return True
rotated_matrix = [row[:] for row in matrix]
for _ in range(3):
# Rotate the matrix 90 degrees clockwise
rotated_matrix = list(zip(*rotated_matrix[::-1]))
#Check if the rotated matrix matches the target
if rotated_matrix == target:
return True
# If none of the rotations match, return False
return FalseBig(O) Analysis
Optimal Solution
Approach
The trick is to realize that rotating a matrix four times brings it back to the original. Therefore, we only need to check three rotations to determine if the target matrix can be obtained. Each rotation involves rearranging elements in a specific way, which we can do by comparing each rotation with the target.
Here's how the algorithm would work step-by-step:
- First, directly compare the original matrix with the target matrix. If they are the same, we're done.
- If they are not the same, rotate the original matrix 90 degrees clockwise.
- Now, compare the rotated matrix with the target matrix. If they match, we have found a valid rotation.
- If they still don't match, rotate the matrix another 90 degrees clockwise (total of 180 degrees from the original).
- Again, compare this new rotation with the target matrix. If they match, we're done.
- If they still don't match, rotate the matrix one more time, 90 degrees clockwise (total of 270 degrees from the original).
- Compare this final rotated matrix with the target. If they match, we're done.
- If none of the rotations match the target matrix, then it's impossible to obtain the target matrix through rotation.
Code Implementation
def determine_if_matrix_can_be_obtained_by_rotation(
matrix, target_matrix):
if matrix == target_matrix:
return True
for _ in range(3):
# Rotate the matrix 90 degrees clockwise
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
rotated_matrix = [([0] * number_of_rows) for _ in range(
number_of_columns)]
for i in range(number_of_rows):
for j in range(number_of_columns):
rotated_matrix[j][number_of_rows - 1 - i] = matrix[i][j]
matrix = rotated_matrix
# Check if the rotated matrix is equal to the target matrix
if matrix == target_matrix:
return True
# No rotation resulted in the target matrix
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix inputs | Return true if both are null/empty; otherwise, return false because rotation isn't applicable or possible. |
| Matrices with different dimensions (not square or different sizes) | Return false immediately because rotation is only defined for square matrices of the same size. |
| 1x1 matrix | Return true if the single element in both matrices is the same, as any rotation yields the same matrix. |
| 2x2 matrix | Explicitly test all four rotations (0, 90, 180, 270 degrees) as this is a small but crucial test case to check rotation logic. |
| Large matrix (performance considerations) | Ensure the rotation logic is efficient (e.g., in-place rotation or using loops with proper index manipulation) to avoid time limit exceeded errors for large input matrices. |
| Matrix containing only identical values | The rotation checks should still function correctly regardless of element values within the matrix. |
| Matrix containing negative, zero, and positive values | The comparison during rotation checks must handle the full range of integer values without type overflow errors. |
| Integer overflow during index calculations in large matrices | Use appropriate data types (e.g., long) for index calculations if the matrix dimensions could potentially lead to overflow. |