Detonate the Maximum Bombs
Detonate the Maximum Bombs #1 Most Asked
MediumYou are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb.
The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range.
You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb.
Example 1:
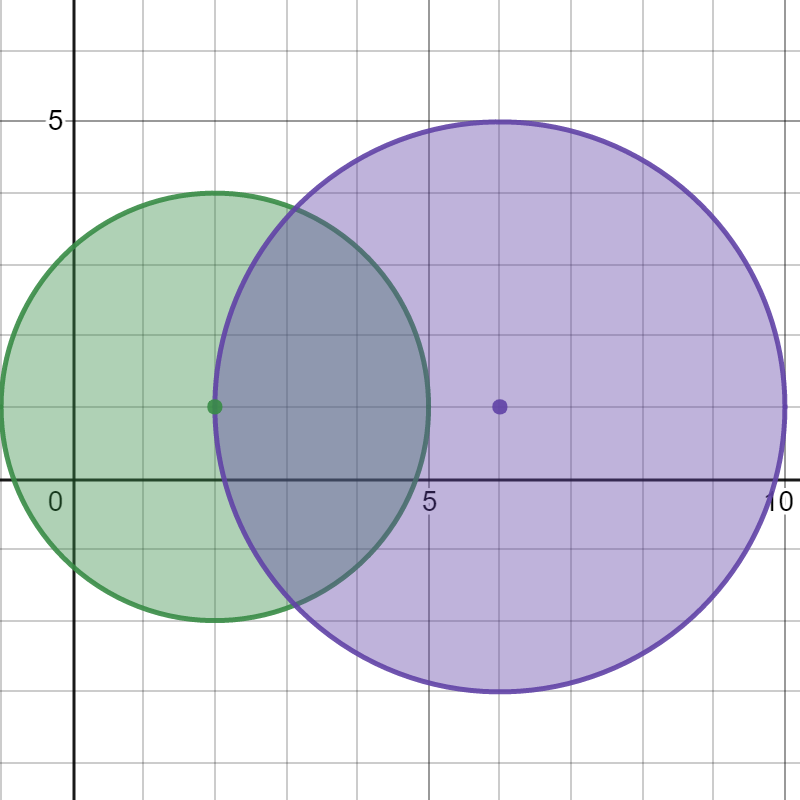
Input: bombs = [[2,1,3],[6,1,4]] Output: 2 Explanation: The above figure shows the positions and ranges of the 2 bombs. If we detonate the left bomb, the right bomb will not be affected. But if we detonate the right bomb, both bombs will be detonated. So the maximum bombs that can be detonated is max(1, 2) = 2.
Example 2:
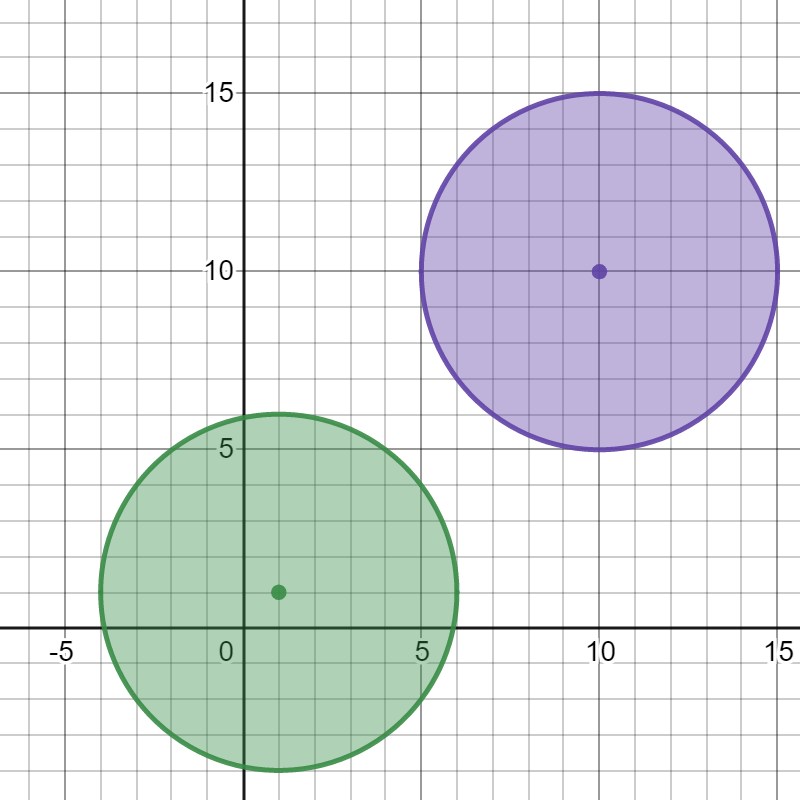
Input: bombs = [[1,1,5],[10,10,5]] Output: 1 Explanation: Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
Example 3:
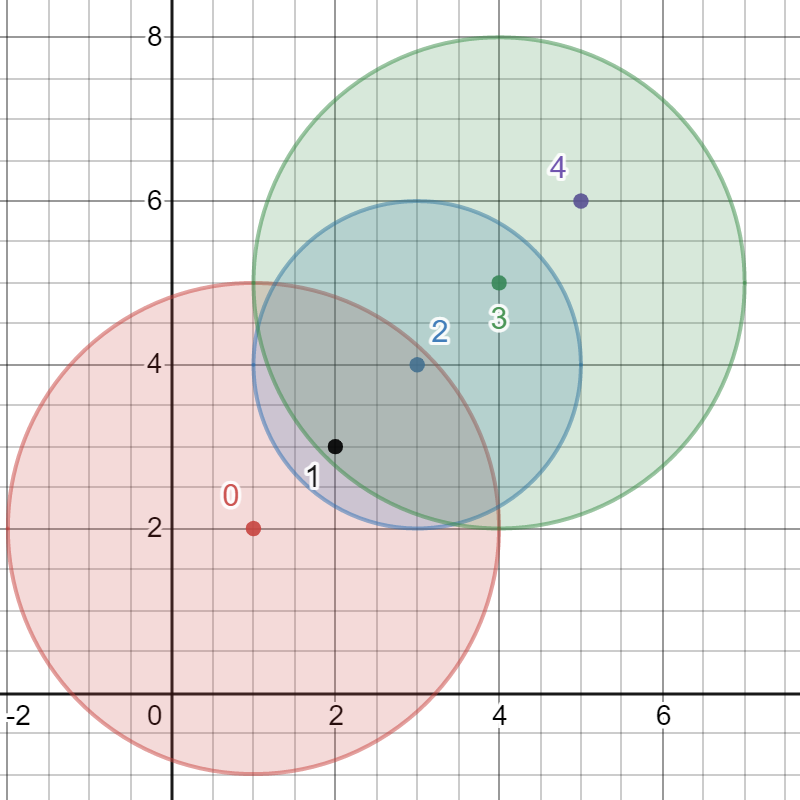
Input: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]] Output: 5 Explanation: The best bomb to detonate is bomb 0 because: - Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0. - Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2. - Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3. Thus all 5 bombs are detonated.
Constraints:
1 <= bombs.length <= 100bombs[i].length == 31 <= xi, yi, ri <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum number of bombs I should expect in the input array?
- Can the radius of a bomb be zero? Can the coordinates of a bomb be negative?
- If detonating a bomb triggers multiple other bombs simultaneously, should I count all the triggered bombs as detonated in the end result?
- Is there a specific data type for the coordinates and radius (e.g., integer or float)?
- If a bomb is on the border of another bomb's radius (distance equals the radius), does it get detonated?
Brute Force Solution
Approach
Imagine each bomb can start a chain reaction. The brute force way is to try setting off each bomb individually and seeing what happens. We detonate each bomb and count how many others explode, then pick the bomb that causes the biggest chain reaction.
Here's how the algorithm would work step-by-step:
- Pick the first bomb on the list.
- Imagine setting off only that bomb. See which other bombs it would explode.
- Count the total number of bombs that would explode in this scenario, including the first bomb you set off.
- Write down that total number.
- Now, pick the second bomb on the list.
- Imagine setting off only the second bomb. See which other bombs it would explode.
- Count the total number of bombs that would explode in this new scenario, including the second bomb.
- Write down this total number as well.
- Repeat this process for every single bomb on the list.
- Finally, look at all the totals you wrote down and find the biggest number. That number represents the maximum number of bombs that can be detonated by setting off a single bomb, and that's the answer.
Code Implementation
def detonate_the_maximum_bombs(bombs):
number_of_bombs = len(bombs)
maximum_bombs_detonated = 0
for bomb_index in range(number_of_bombs):
# Simulate detonating each bomb and counting the chain reaction.
bombs_detonated_count = detonate_bombs(bomb_index, bombs)
maximum_bombs_detonated = max(maximum_bombs_detonated, bombs_detonated_count)
return maximum_bombs_detonated
def detonate_bombs(starting_bomb_index, bombs):
number_of_bombs = len(bombs)
exploded = [False] * number_of_bombs
queue = [starting_bomb_index]
exploded[starting_bomb_index] = True
count = 0
while queue:
bomb_index = queue.pop(0)
count += 1
bomb_x, bomb_y, bomb_radius = bombs[bomb_index]
# Check each bomb to see if its within the radius
for next_bomb_index in range(number_of_bombs):
if not exploded[next_bomb_index]:
next_bomb_x, next_bomb_y, _ = bombs[next_bomb_index]
distance_squared = (next_bomb_x - bomb_x) ** 2 + (next_bomb_y - bomb_y) ** 2
# If within radius, add to the queue for explosion.
if distance_squared <= bomb_radius ** 2:
queue.append(next_bomb_index)
exploded[next_bomb_index] = True
return countBig(O) Analysis
Optimal Solution
Approach
The problem is about figuring out the biggest chain reaction we can cause by setting off bombs. Instead of randomly trying every combination, we’ll figure out which bombs affect which other bombs and then explore the chain reactions systematically, starting from each bomb individually.
Here's how the algorithm would work step-by-step:
- First, figure out which bombs will set off which other bombs. Imagine each bomb has an area around it – if another bomb is inside that area, the first bomb will detonate it.
- Think of the bombs and their connections as a network. Each bomb can reach other bombs directly, or indirectly through other bombs.
- For each bomb, pretend we set it off first. Trace all the other bombs it would detonate, and then all the bombs those would detonate, and so on. Count how many bombs go off in total when starting from this specific bomb.
- Repeat this process for every bomb in the list. Keep track of the largest number of bombs detonated in any of these chain reactions.
- The largest number you kept track of in the previous steps is the answer: the maximum number of bombs that can be detonated.
Code Implementation
def detonate_the_maximum_bombs(bombs):
number_of_bombs = len(bombs)
def is_within_range(bomb_one, bomb_two):
x1, y1, radius1 = bomb_one
x2, y2, radius2 = bomb_two
distance_squared = (x2 - x1)**2 + (y2 - y1)**2
return distance_squared <= radius1**2
# Build adjacency list representing bomb connections
adjacency_list = [[] for _ in range(number_of_bombs)]
for i in range(number_of_bombs):
for j in range(number_of_bombs):
if i != j and is_within_range(bombs[i], bombs[j]):
adjacency_list[i].append(j)
def detonate_bombs(starting_bomb):
# Use a set to track detonated bombs
detonated = set()
queue = [starting_bomb]
detonated.add(starting_bomb)
while queue:
current_bomb = queue.pop(0)
for neighbor in adjacency_list[current_bomb]:
# Only detonate if not already detonated
if neighbor not in detonated:
detonated.add(neighbor)
queue.append(neighbor)
return len(detonated)
max_bombs_detonated = 0
# Iterate through each bomb as the starting point
for i in range(number_of_bombs):
max_bombs_detonated = max(max_bombs_detonated, detonate_bombs(i))
return max_bombs_detonatedBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty bombs array | Return 0 as no bombs can be detonated. |
| Single bomb in the array | Return 1 as detonating the single bomb will detonate one bomb. |
| All bombs are located at the exact same coordinates. | Detonating any bomb detonates all bombs, so return the number of bombs. |
| Bomb radii are very large, causing integer overflow when calculating distances | Use long data types for distance calculations to prevent integer overflow. |
| Bombs are arranged in a long chain, where each bomb only detonates the next bomb in the chain | The graph traversal must explore the full depth of the chain to count all bombs. |
| Bombs are arranged in a dense cluster, with each bomb capable of detonating many others | The solution should efficiently track visited nodes to avoid redundant computations. |
| Bombs do not form any connected components | Iterate through all bombs and check if detonating each bomb yields a different number of detonations, then take the maximum. |
| Input array with large number of bombs (close to constraints limit) | Check for time complexity issues, which can be improved by using an efficient data structure/algorithm. |