Escape the Spreading Fire
HardYou are given a 0-indexed 2D integer array grid of size m x n which represents a field. Each cell has one of three values:
0represents grass,1represents fire,2represents a wall that you and fire cannot pass through.
You are situated in the top-left cell, (0, 0), and you want to travel to the safehouse at the bottom-right cell, (m - 1, n - 1). Every minute, you may move to an adjacent grass cell. After your move, every fire cell will spread to all adjacent cells that are not walls.
Return the maximum number of minutes that you can stay in your initial position before moving while still safely reaching the safehouse. If this is impossible, return -1. If you can always reach the safehouse regardless of the minutes stayed, return 109.
Note that even if the fire spreads to the safehouse immediately after you have reached it, it will be counted as safely reaching the safehouse.
A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).
Example 1:
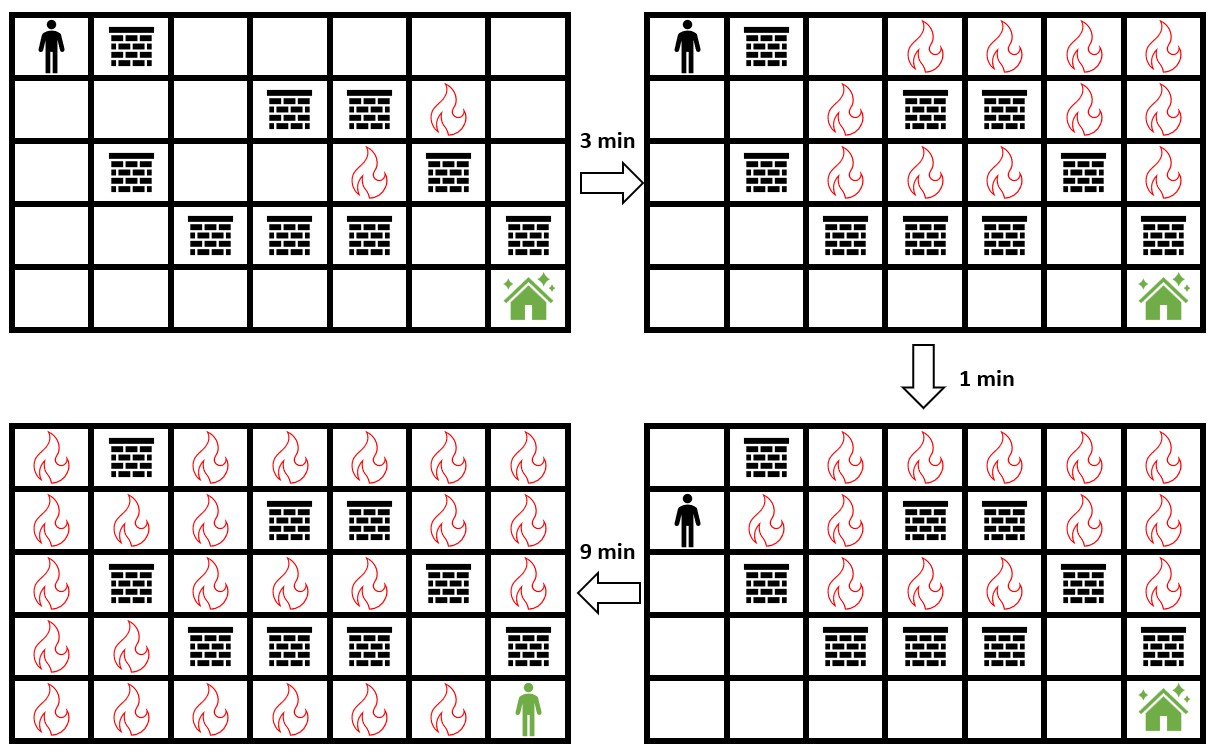
Input: grid = [[0,2,0,0,0,0,0],[0,0,0,2,2,1,0],[0,2,0,0,1,2,0],[0,0,2,2,2,0,2],[0,0,0,0,0,0,0]] Output: 3 Explanation: The figure above shows the scenario where you stay in the initial position for 3 minutes. You will still be able to safely reach the safehouse. Staying for more than 3 minutes will not allow you to safely reach the safehouse.
Example 2:
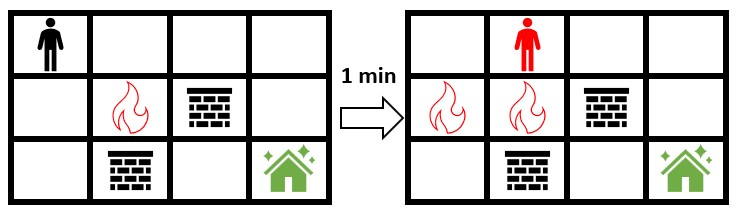
Input: grid = [[0,0,0,0],[0,1,2,0],[0,2,0,0]] Output: -1 Explanation: The figure above shows the scenario where you immediately move towards the safehouse. Fire will spread to any cell you move towards and it is impossible to safely reach the safehouse. Thus, -1 is returned.
Example 3:
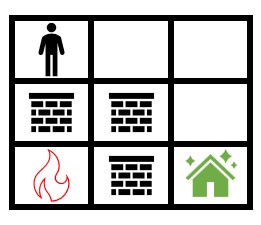
Input: grid = [[0,0,0],[2,2,0],[1,2,0]] Output: 1000000000 Explanation: The figure above shows the initial grid. Notice that the fire is contained by walls and you will always be able to safely reach the safehouse. Thus, 109 is returned.
Constraints:
m == grid.lengthn == grid[i].length2 <= m, n <= 3004 <= m * n <= 2 * 104grid[i][j]is either0,1, or2.grid[0][0] == grid[m - 1][n - 1] == 0
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid, and what is the maximum value for any cell representing fire spread time?
- What is the representation of the grid? Is it a 2D array of integers? What do different integer values signify (e.g., 0 for empty, 1 for grass, 2 for fire)?
- Where does the person start, and where is the safehouse located? Are these locations fixed, or are they part of the input?
- If it's impossible to escape the fire, what should I return?
- How does the fire spread? Does it spread to adjacent cells (up, down, left, right) simultaneously at each time step, or is there a delay?
Brute Force Solution
Approach
The brute force method involves trying every possible waiting time to see if we can safely reach the destination. We'll test each possible delay, then simulate the fire spreading and our movement to see if escape is possible with that delay.
Here's how the algorithm would work step-by-step:
- Start with waiting for no time at all before moving.
- Simulate the fire spreading and your movement simultaneously. Check if the fire ever reaches you before you reach the destination.
- If the fire reaches you first, then waiting for zero time will not work.
- Now, try waiting for one unit of time before moving. Again, simulate the fire spreading and your movement.
- Check if the fire reaches you before you reach the destination.
- Repeat this process, increasing the waiting time by one unit each time.
- Continue until you find a waiting time that allows you to reach the destination before the fire does.
- If you've tried waiting for a very, very long time (like, longer than the size of the grid) and you still can't escape, then it's impossible to escape no matter how long you wait.
Code Implementation
def escape_the_spreading_fire_brute_force(forest):
rows = len(forest)
cols = len(forest[0])
def is_safe(wait_time):
# Simulate fire and person movement with the given wait time.
fire_grid = [row[:] for row in forest]
person_grid = [row[:] for row in forest]
# Mark starting positions.
start_row, start_col = 0, 0
destination_row, destination_col = rows - 1, cols - 1
queue = []
for row_index in range(rows):
for col_index in range(cols):
if forest[row_index][col_index] == 1:
queue.append((row_index, col_index, 0))
# Spread the fire.
fire_spread_time = [[float('inf')] * cols for _ in range(rows)]
for row_index in range(rows):
for col_index in range(cols):
if forest[row_index][col_index] == 1:
fire_spread_time[row_index][col_index] = 0
fire_directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
while queue:
row_index, col_index, time = queue.pop(0)
for direction_row, direction_col in fire_directions:
new_row = row_index + direction_row
new_col = col_index + direction_col
if 0 <= new_row < rows and 0 <= new_col < cols and \
forest[new_row][new_col] != 2 and time + 1 < fire_spread_time[new_row][new_col]:
fire_spread_time[new_row][new_col] = time + 1
queue.append((new_row, new_col, time + 1))
# Calculate person's path after waiting
person_spread_time = [[float('inf')] * cols for _ in range(rows)]
person_spread_time[0][0] = wait_time
queue = [(0, 0, wait_time)]
person_directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
while queue:
row_index, col_index, time = queue.pop(0)
for direction_row, direction_col in person_directions:
new_row = row_index + direction_row
new_col = col_index + direction_col
if 0 <= new_row < rows and 0 <= new_col < cols and \
forest[new_row][new_col] != 2 and time + 1 < person_spread_time[new_row][new_col]:
person_spread_time[new_row][new_col] = time + 1
queue.append((new_row, new_col, time + 1))
# Determine if escape is possible. Compare fire and person times
return person_spread_time[destination_row][destination_col] <= fire_spread_time[destination_row][destination_col]
# Test increasing wait times until escape is possible.
max_wait_time = rows * cols
for wait_time in range(max_wait_time + 1):
if is_safe(wait_time):
return wait_time
# If we tried all possibilities, escape is impossible
return -1Big(O) Analysis
Optimal Solution
Approach
This problem involves figuring out the latest moment you can reach a safehouse before the fire does. The core idea is to determine if reaching the safehouse is possible at a given time. We use a technique that helps us quickly check the feasibility of reaching the safehouse at different times, instead of simulating the entire process repeatedly.
Here's how the algorithm would work step-by-step:
- First, realize the fire spreads outwards, so we can calculate how much time it takes for the fire to reach any spot on the map.
- Next, instead of guessing and checking one time at a time, consider a broader question: 'Can I reach the safehouse if I start at a specific time?'
- To answer this, figure out how long it takes you to reach a specific location (such as the safehouse) from the starting point.
- Compare the time it takes for you to reach a location with the time it takes for the fire to reach that same location. If you arrive earlier than the fire, that location is safe to pass through.
- Use a common path-finding technique to determine if there is a valid, safe path from your starting position to the safehouse, considering the arrival times of the fire at each location.
- Instead of checking each possible starting time individually, we'll use an approach to efficiently search for the maximum possible starting time. If reaching the safe house is impossible immediately, the answer is -1. If we can reach the safe house even when the fire never spreads, the answer is infinity.
- If reaching the safe house is possible immediately but impossible if the fire never spreads, we can use a method to efficiently narrow down the possible starting times to find the latest time we can start and still escape.
Code Implementation
from collections import deque
def escape_the_spreading_fire(grid):
rows = len(grid)
cols = len(grid[0])
def find_start_and_safehouse(grid):
start = None
safehouse = None
for row in range(rows):
for col in range(cols):
if grid[row][col] == 0:
if start is None:
start = (row, col)
else:
safehouse = (row, col)
return start, safehouse
start_position, safehouse_position = find_start_and_safehouse(grid)
def calculate_fire_arrival_times(grid):
rows = len(grid)
cols = len(grid[0])
fire_arrival_times = [[float('inf')] * cols for _ in range(rows)]
fire_queue = deque()
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
fire_arrival_times[row][col] = 0
fire_queue.append((row, col))
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
time = 1
while fire_queue:
level_size = len(fire_queue)
for _ in range(level_size):
row, col = fire_queue.popleft()
for d_row, d_col in directions:
new_row, new_col = row + d_row, col + d_col
if 0 <= new_row < rows and 0 <= new_col < cols and \
fire_arrival_times[new_row][new_col] == float('inf') and grid[new_row][new_col] != 2:
fire_arrival_times[new_row][new_col] = time
fire_queue.append((new_row, new_col))
time += 1
return fire_arrival_times
fire_arrival_times = calculate_fire_arrival_times(grid)
def is_safe_path(start_time, fire_arrival_times, grid, start_position, safehouse_position):
rows = len(grid)
cols = len(grid[0])
player_arrival_times = [[float('inf')] * cols for _ in range(rows)]
player_queue = deque()
player_queue.append((start_position[0], start_position[1], start_time))
player_arrival_times[start_position[0]][start_position[1]] = start_time
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
while player_queue:
row, col, time = player_queue.popleft()
if (row, col) == safehouse_position:
return True
for d_row, d_col in directions:
new_row, new_col = row + d_row, col + d_col
if 0 <= new_row < rows and 0 <= new_col < cols and grid[new_row][new_col] != 2:
new_time = time + 1
# Check if the player arrives before the fire
if new_time < fire_arrival_times[new_row][new_col] and new_time < player_arrival_times[new_row][new_col]:
player_arrival_times[new_row][new_col] = new_time
player_queue.append((new_row, new_col, new_time))
return False
# If it is impossible to reach the safehouse initially, return -1.
if not is_safe_path(0, fire_arrival_times, grid, start_position, safehouse_position):
return -1
# Check for infinite wait time
temp_fire_arrival_times = [[float('inf')] * cols for _ in range(rows)]
if is_safe_path(10**9, temp_fire_arrival_times, grid, start_position, safehouse_position):
return 10**9
left_wait_time = 0
right_wait_time = 10**9
latest_possible_time = 0
# Binary search for the maximum possible start time
while left_wait_time <= right_wait_time:
mid_wait_time = left_wait_time + (right_wait_time - left_wait_time) // 2
if is_safe_path(mid_wait_time, fire_arrival_times, grid, start_position, safehouse_position):
latest_possible_time = mid_wait_time
left_wait_time = mid_wait_time + 1
else:
right_wait_time = mid_wait_time - 1
return latest_possible_timeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Grid is null or empty (0x0) | Return -1 immediately, indicating impossible escape. |
| Grid is 1x1 with the start at (0,0) and no fire | Return 0, since the person is already at the safehouse. |
| Person's starting position is immediately on fire | Return -1, since the person cannot survive. |
| Fire cannot reach the safe house and the person can reach the safe house | Return infinity, since the person can indefinitely wait to escape |
| Fire spreads faster than the person can move to the safehouse | Return 0, since the person has no delay to wait. |
| The safehouse is unreachable by the person | Return -1, indicating impossible escape. |
| Integer overflow when calculating fire or person spread times in large grids | Use long or appropriate data type to store the time/distance values to prevent overflow. |
| Grid with all fire cells initially | Return -1 immediately, as there is no escape possible. |