Exclusive Time of Functions
Exclusive Time of Functions #2 Most Asked
MediumOn a single-threaded CPU, we execute a program containing n functions. Each function has a unique ID between 0 and n-1.
Function calls are stored in a call stack: when a function call starts, its ID is pushed onto the stack, and when a function call ends, its ID is popped off the stack. The function whose ID is at the top of the stack is the current function being executed. Each time a function starts or ends, we write a log with the ID, whether it started or ended, and the timestamp.
You are given a list logs, where logs[i] represents the ith log message formatted as a string "{function_id}:{"start" | "end"}:{timestamp}". For example, "0:start:3" means a function call with function ID 0 started at the beginning of timestamp 3, and "1:end:2" means a function call with function ID 1 ended at the end of timestamp 2. Note that a function can be called multiple times, possibly recursively.
A function's exclusive time is the sum of execution times for all function calls in the program. For example, if a function is called twice, one call executing for 2 time units and another call executing for 1 time unit, the exclusive time is 2 + 1 = 3.
Return the exclusive time of each function in an array, where the value at the ith index represents the exclusive time for the function with ID i.
Example 1:
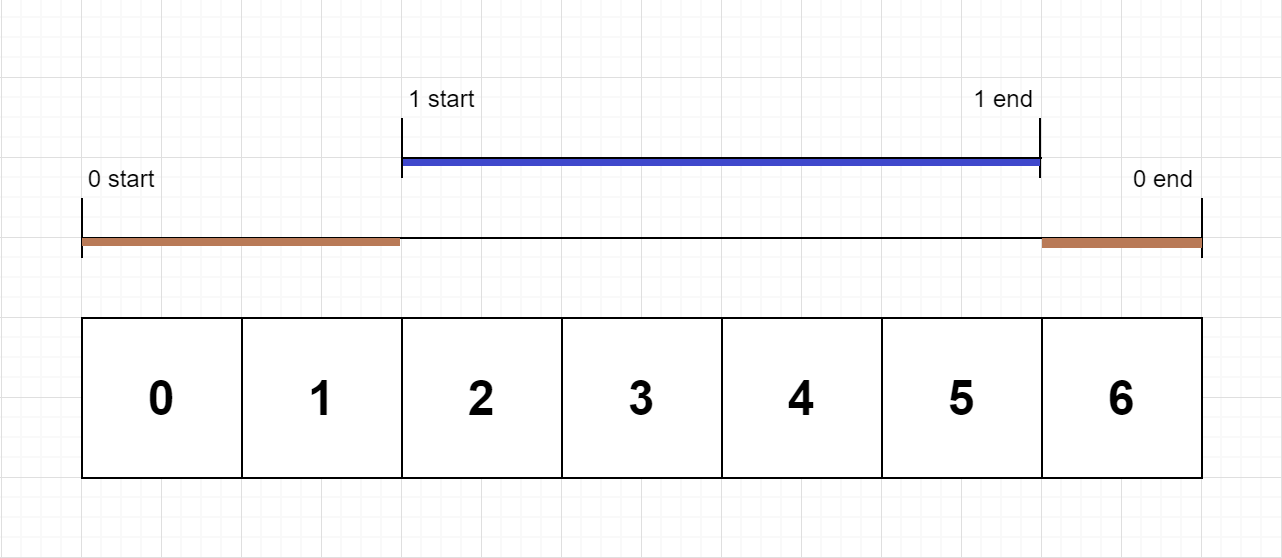
Input: n = 2, logs = ["0:start:0","1:start:2","1:end:5","0:end:6"] Output: [3,4] Explanation: Function 0 starts at the beginning of time 0, then it executes 2 for units of time and reaches the end of time 1. Function 1 starts at the beginning of time 2, executes for 4 units of time, and ends at the end of time 5. Function 0 resumes execution at the beginning of time 6 and executes for 1 unit of time. So function 0 spends 2 + 1 = 3 units of total time executing, and function 1 spends 4 units of total time executing.
Example 2:
Input: n = 1, logs = ["0:start:0","0:start:2","0:end:5","0:start:6","0:end:6","0:end:7"] Output: [8] Explanation: Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself. Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time. Function 0 (initial call) resumes execution then immediately calls itself again. Function 0 (2nd recursive call) starts at the beginning of time 6 and executes for 1 unit of time. Function 0 (initial call) resumes execution at the beginning of time 7 and executes for 1 unit of time. So function 0 spends 2 + 4 + 1 + 1 = 8 units of total time executing.
Example 3:
Input: n = 2, logs = ["0:start:0","0:start:2","0:end:5","1:start:6","1:end:6","0:end:7"] Output: [7,1] Explanation: Function 0 starts at the beginning of time 0, executes for 2 units of time, and recursively calls itself. Function 0 (recursive call) starts at the beginning of time 2 and executes for 4 units of time. Function 0 (initial call) resumes execution then immediately calls function 1. Function 1 starts at the beginning of time 6, executes 1 unit of time, and ends at the end of time 6. Function 0 resumes execution at the beginning of time 6 and executes for 2 units of time. So function 0 spends 2 + 4 + 1 = 7 units of total time executing, and function 1 spends 1 unit of total time executing.
Constraints:
1 <= n <= 1002 <= logs.length <= 5000 <= function_id < n0 <= timestamp <= 109- No two start events will happen at the same timestamp.
- No two end events will happen at the same timestamp.
- Each function has an
"end"log for each"start"log.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of possible thread IDs, and are they guaranteed to be non-negative integers?
- What is the format of the log entries? Specifically, can I assume the format is always "{function_id}:START_OR_END:{timestamp}"?
- If a function is still running when the input ends (i.e., there's a START but no corresponding END), how should I calculate its exclusive time?
- Can function IDs be non-sequential, or are they guaranteed to be a contiguous range starting from 0?
- Can I assume the input logs are chronologically sorted by timestamp, or do I need to handle out-of-order log entries?
Brute Force Solution
Approach
We need to figure out how much time each function spends running, given logs of when they start and stop. The brute force way is like simulating the entire execution, second by second, and tracking which function is running at each moment. It's like watching the whole process unfold.
Here's how the algorithm would work step-by-step:
- Go through the logs one by one.
- For each second of the execution, check which function is active based on the start and end times.
- If a function is running during that second, add one to its running time.
- Repeat this process for every single second covered by the logs.
- Once you have gone through all the seconds, you'll know the total running time for each function.
Code Implementation
def exclusive_time_brute_force(number_of_functions, logs):
function_execution_times = [0] * number_of_functions
current_time = 0
log_entries = []
for log in logs:
function_id, event_type, timestamp = log.split(":")
log_entries.append((int(function_id), event_type, int(timestamp)))
while True:
current_function = -1
# Find the currently running function.
for function_id in range(number_of_functions):
start_found = False
end_found = False
start_time = -1
end_time = -1
for function_id_log, event_type, timestamp in log_entries:
if function_id_log == function_id:
if event_type == "start" and timestamp <= current_time:
start_found = True
start_time = timestamp
if event_type == "end" and timestamp >= current_time:
end_found = True
end_time = timestamp
if start_found and not end_found:
current_function = function_id
break
if current_function != -1:
function_execution_times[current_function] += 1
# Check if all logs have been processed to stop the simulation.
all_logs_processed = True
max_time = -1
for function_id, event_type, timestamp in log_entries:
max_time = max(max_time, timestamp)
if current_time > max_time:
all_logs_processed = True
else:
all_logs_processed = False
if all_logs_processed and current_function == -1:
break
current_time += 1
return function_execution_timesBig(O) Analysis
Optimal Solution
Approach
To efficiently calculate the exclusive time of functions, we can use a stack to track the currently executing function. When a function starts, we push it onto the stack, and when it ends, we pop it. The exclusive time is calculated by tracking the durations between start and end logs, taking into account nested function calls.
Here's how the algorithm would work step-by-step:
- We'll use a container to keep track of which function is currently running.
- When we see a function starting, we record the exact moment it begins.
- Before a new function begins, if we have a function currently running, we calculate how long it has been running so far and add it to that function's total running time.
- When a function ends, we calculate how long it ran and add that to its total running time.
- Remember to update the start time whenever a new function starts, or a function ends and we resume the function that was previously running.
- By the end, we'll have the total exclusive running time for each function.
Code Implementation
def get_exclusive_time(number_of_functions, logs):
exclusive_times = [0] * number_of_functions
stack_of_functions = []
previous_time = 0
for log in logs:
function_id, operation, timestamp = log.split(':')
function_id = int(function_id)
timestamp = int(timestamp)
if operation == 'start':
# Account for time elapsed in the previous function
if stack_of_functions:
exclusive_times[stack_of_functions[-1]] += timestamp - previous_time
stack_of_functions.append(function_id)
previous_time = timestamp
else:
# Accumulate time for current function and update the time
exclusive_times[function_id] += timestamp - previous_time + 1
stack_of_functions.pop()
previous_time = timestamp + 1
# Update previous_time after end
return exclusive_timesBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty logs array | Return an empty list or an array of zeros of appropriate size to indicate no execution time. |
| Logs array with only 'start' events and no corresponding 'end' events. | Handle incomplete function calls by ignoring the 'start' events at the end or assuming they end at the end of the entire log. |
| Logs array with only 'end' events and no corresponding 'start' events. | Ignore such 'end' events since they are invalid without a matching 'start'. |
| Nested function calls that overlap (e.g., function A starts, then function B starts, then function A ends, then function B ends). | The stack-based approach should correctly handle overlapping calls by assigning exclusive time based on the current top of the stack. |
| Number of functions (n) is very large, potentially leading to large result array allocation. | Ensure memory is allocated dynamically and efficiently; consider a more memory-efficient data structure if scaling becomes a problem. |
| Log timestamps are not strictly increasing. | Sort the log entries by timestamp before processing to ensure correct time calculation, or throw an error if non-increasing logs are considered invalid. |
| Integer overflow in calculating execution time differences. | Use long integers or appropriate data types to avoid integer overflow when calculating differences in timestamps. |
| Function calls that start and end at the same timestamp. | Handle zero-duration calls correctly by ensuring the time difference calculation is accurate (end_time - start_time + 1 when appropriate). |