Falling Squares #7 Most Asked
HardThere are several squares being dropped onto the X-axis of a 2D plane.
You are given a 2D integer array positions where positions[i] = [lefti, sideLengthi] represents the ith square with a side length of sideLengthi that is dropped with its left edge aligned with X-coordinate lefti.
Each square is dropped one at a time from a height above any landed squares. It then falls downward (negative Y direction) until it either lands on the top side of another square or on the X-axis. A square brushing the left/right side of another square does not count as landing on it. Once it lands, it freezes in place and cannot be moved.
After each square is dropped, you must record the height of the current tallest stack of squares.
Return an integer array ans where ans[i] represents the height described above after dropping the ith square.
Example 1:
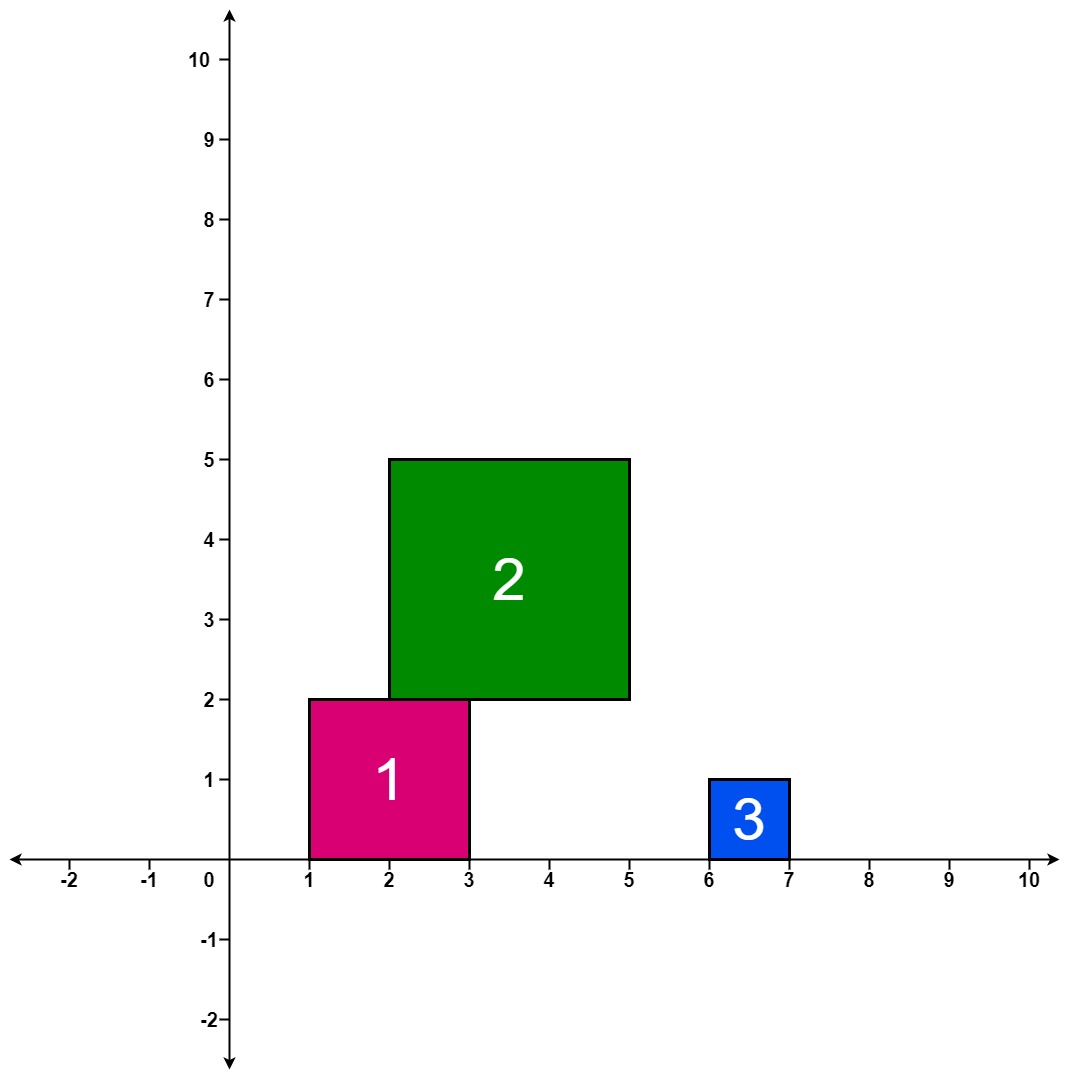
Input: positions = [[1,2],[2,3],[6,1]] Output: [2,5,5] Explanation: After the first drop, the tallest stack is square 1 with a height of 2. After the second drop, the tallest stack is squares 1 and 2 with a height of 5. After the third drop, the tallest stack is still squares 1 and 2 with a height of 5. Thus, we return an answer of [2, 5, 5].
Example 2:
Input: positions = [[100,100],[200,100]] Output: [100,100] Explanation: After the first drop, the tallest stack is square 1 with a height of 100. After the second drop, the tallest stack is either square 1 or square 2, both with heights of 100. Thus, we return an answer of [100, 100]. Note that square 2 only brushes the right side of square 1, which does not count as landing on it.
Constraints:
1 <= positions.length <= 10001 <= lefti <= 1081 <= sideLengthi <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the `positions` array size and the side length of each square? Is there a maximum value?
- Can the coordinates in the `positions` array be negative or zero?
- If squares overlap, how is the height at the overlapping position determined (e.g., is it the sum of the heights or the maximum of the heights)?
- Is the order of squares in the `positions` array the order in which they are dropped?
- What should the output be if the `positions` array is empty?
Brute Force Solution
Approach
The problem involves dropping squares onto a line and figuring out the height at each drop. The brute force approach simulates each drop and then meticulously recalculates the entire skyline after each square lands to determine the maximum height at that point.
Here's how the algorithm would work step-by-step:
- Imagine a blank canvas representing the line. We will draw the fallen squares onto it.
- For each new square that falls, figure out where its left edge lands on the line.
- Check if the new square overlaps with any of the previously fallen squares. Overlapping means any horizontal part of the new square occupies the same space as the horizontal part of a previous square.
- If the new square overlaps, figure out how high the existing squares are at the location where the new square is going to fall. The highest of these heights determines the 'ground' for the new square.
- Place the new square on the canvas, its bottom touching the ground level calculated in the previous step.
- After placing the square, re-examine the entire canvas to determine the maximum height achieved so far. This is the height after that particular drop.
- Record this maximum height.
- Repeat this process for each square that falls, keeping track of the maximum height after each drop.
Code Implementation
def falling_squares_brute_force(positions):
fallen_squares = []
heights = []
for position in positions:
left_edge = position[0]
side_length = position[1]
right_edge = left_edge + side_length
# Determine the ground level for the new square.
ground_level = 0
for fallen_left, fallen_side, fallen_height in fallen_squares:
fallen_right = fallen_left + fallen_side
# Check for overlap
if max(left_edge, fallen_left) < min(right_edge, fallen_right):
ground_level = max(ground_level, fallen_height)
new_height = ground_level + side_length
fallen_squares.append((left_edge, side_length, new_height))
# Recalculate the maximum height after the new square falls.
max_height = 0
for fallen_left, fallen_side, fallen_height in fallen_squares:
max_height = max(max_height, fallen_height)
heights.append(max_height)
return heightsBig(O) Analysis
Optimal Solution
Approach
The problem involves stacking squares and figuring out the highest point after each square falls. The efficient solution cleverly tracks the covered intervals on the 'ground' to determine how high each new square will land and update the overall maximum height.
Here's how the algorithm would work step-by-step:
- Imagine the ground is initially flat at height zero everywhere.
- When a square falls, determine where it lands on the ground.
- To do this, check what existing 'ground' intervals the falling square overlaps with.
- The height at which the square lands will be the maximum height of the ground intervals it overlaps.
- After the square lands, it creates a new ground interval with a height equal to the landing height plus the side length of the square.
- Importantly, the new interval may overlap and replace existing intervals, either partially or fully.
- Combine or remove any existing intervals that overlap with the newly landed square to correctly reflect the new ground profile.
- The maximum height is updated to include the highest point reached at each step as squares fall.
- By tracking and merging intervals, we can quickly determine the landing height and update the ground profile without exhaustively checking every position.
Code Implementation
def fallingSquares(positions):
groundIntervals = []
maxHeight = 0
result = []
for position in positions:
left = position[0]
sideLength = position[1]
right = left + sideLength
currentHeight = 0
# Find the max height in the overlapping intervals.
for intervalLeft, intervalRight, intervalHeight in groundIntervals:
if left < intervalRight and intervalLeft < right:
currentHeight = max(currentHeight, intervalHeight)
newHeight = currentHeight + sideLength
maxHeight = max(maxHeight, newHeight)
result.append(maxHeight)
newIntervals = []
i = 0
# Merge overlapping intervals and create new ones.
while i < len(groundIntervals):
intervalLeft = groundIntervals[i][0]
intervalRight = groundIntervals[i][1]
intervalHeight = groundIntervals[i][2]
if intervalRight <= left or right <= intervalLeft:
newIntervals.append((intervalLeft, intervalRight, intervalHeight))
else:
if intervalLeft < left:
newIntervals.append((intervalLeft, left, intervalHeight))
if right < intervalRight:
newIntervals.append((right, intervalRight, intervalHeight))
i += 1
newIntervals.append((left, right, newHeight))
newIntervals.sort()
groundIntervals = []
if newIntervals:
groundIntervals.append(newIntervals[0])
for i in range(1, len(newIntervals)):
prevIntervalLeft, prevIntervalRight, prevIntervalHeight = groundIntervals[-1]
currentIntervalLeft, currentIntervalRight, currentIntervalHeight = newIntervals[i]
# Combine adjacent intervals of same height
if currentIntervalLeft == prevIntervalRight and currentIntervalHeight == prevIntervalHeight:
groundIntervals[-1] = (prevIntervalLeft, currentIntervalRight, prevIntervalHeight)
else:
groundIntervals.append((currentIntervalLeft, currentIntervalRight, currentIntervalHeight))
return resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty squares array | Return an empty result list if the input squares array is empty. |
| Squares with zero side length | Treat a square with zero side length as having no effect on the skyline. |
| Overlapping squares covering the entire range | Ensure the maximum height is calculated correctly after multiple fully overlapping squares. |
| Very large coordinates leading to integer overflow | Use long to store coordinates and heights to prevent potential integer overflow. |
| Maximum number of squares, stressing memory allocation | Consider using a more memory-efficient data structure if the number of squares is extremely large. |
| Squares with identical positions but different side lengths | The square with a later start position will overwrite any existing heights in the covered range. |
| Squares placed very far apart, leading to large gaps | The solution must accurately represent the skyline even with large gaps of zero height. |
| Negative coordinate values | Adjust coordinate system to handle negative coordinates by offsetting all values to be positive |