Find All Groups of Farmland #3 Most Asked

Medium

1 view

Topics:

ArraysGraphs

You are given a 0-indexed m x n binary matrix land where a 0 represents a hectare of forested land and a 1 represents a hectare of farmland.

To keep the land organized, there are designated rectangular areas of hectares that consist entirely of farmland. These rectangular areas are called groups. No two groups are adjacent, meaning farmland in one group is not four-directionally adjacent to another farmland in a different group.

land can be represented by a coordinate system where the top left corner of land is (0, 0) and the bottom right corner of land is (m-1, n-1). Find the coordinates of the top left and bottom right corner of each group of farmland. A group of farmland with a top left corner at (r₁, c₁) and a bottom right corner at (r₂, c₂) is represented by the 4-length array [r₁, c₁, r₂, c₂].

Return a 2D array containing the 4-length arrays described above for each group of farmland in land. If there are no groups of farmland, return an empty array. You may return the answer in any order.

Example 1:

Input: land = [[1,0,0],[0,1,1],[0,1,1]]
Output: [[0,0,0,0],[1,1,2,2]]
Explanation:
The first group has a top left corner at land[0][0] and a bottom right corner at land[0][0].
The second group has a top left corner at land[1][1] and a bottom right corner at land[2][2].

Example 2:

Input: land = [[1,1],[1,1]]
Output: [[0,0,1,1]]
Explanation:
The first group has a top left corner at land[0][0] and a bottom right corner at land[1][1].

Example 3:

Input: land = [[0]]
Output: []
Explanation:
There are no groups of farmland.

Constraints:

m == land.length
n == land[i].length
1 <= m, n <= 300
land consists of only 0's and 1's.
Groups of farmland are rectangular in shape.

Try coding it in LeetCode

Find All Groups of Farmland #3 Most Asked

Medium

Citrix

1 view

Topics:

ArraysGraphs

You are given a 0-indexed m x n binary matrix land where a 0 represents a hectare of forested land and a 1 represents a hectare of farmland.

To keep the land organized, there are designated rectangular areas of hectares that consist entirely of farmland. These rectangular areas are called groups. No two groups are adjacent, meaning farmland in one group is not four-directionally adjacent to another farmland in a different group.

land can be represented by a coordinate system where the top left corner of land is (0, 0) and the bottom right corner of land is (m-1, n-1). Find the coordinates of the top left and bottom right corner of each group of farmland. A group of farmland with a top left corner at (r₁, c₁) and a bottom right corner at (r₂, c₂) is represented by the 4-length array [r₁, c₁, r₂, c₂].

Return a 2D array containing the 4-length arrays described above for each group of farmland in land. If there are no groups of farmland, return an empty array. You may return the answer in any order.

Example 1:

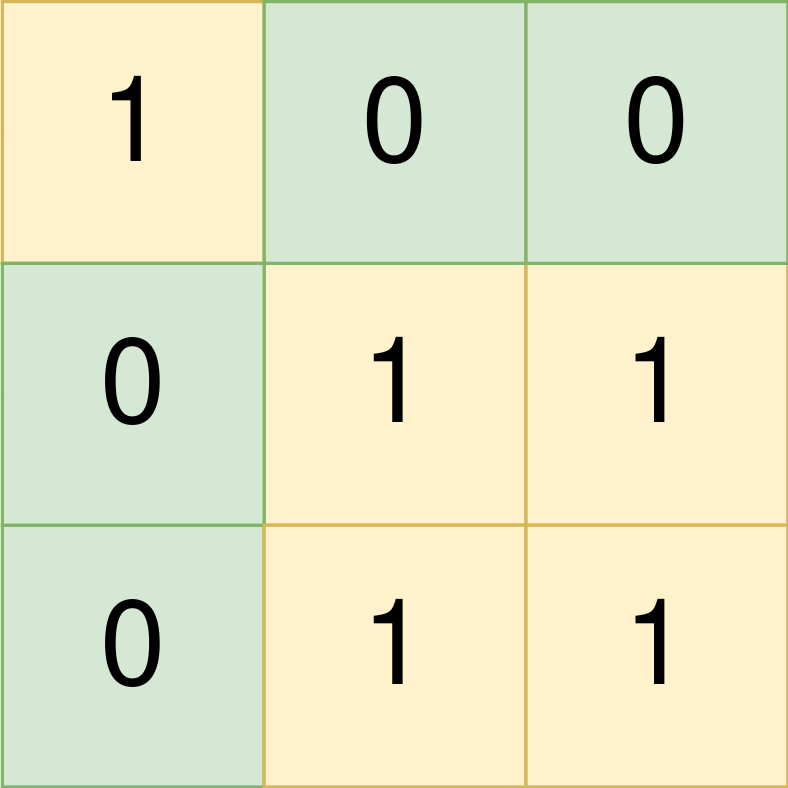
Input: land = [[1,0,0],[0,1,1],[0,1,1]]
Output: [[0,0,0,0],[1,1,2,2]]
Explanation:
The first group has a top left corner at land[0][0] and a bottom right corner at land[0][0].
The second group has a top left corner at land[1][1] and a bottom right corner at land[2][2].

Example 2:

Input: land = [[1,1],[1,1]]
Output: [[0,0,1,1]]
Explanation:
The first group has a top left corner at land[0][0] and a bottom right corner at land[1][1].

Example 3:

Input: land = [[0]]
Output: []
Explanation:
There are no groups of farmland.

Constraints:

m == land.length
n == land[i].length
1 <= m, n <= 300
land consists of only 0's and 1's.
Groups of farmland are rectangular in shape.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the farmland grid, and what is the maximum size of the grid?
What integer values are possible in the grid? Is it guaranteed to only contain 0s and 1s, or could there be other values?
If there are no farmland groups present in the grid, what should the function return? Should it return an empty array?
Is it possible for farmland groups to be adjacent to each other horizontally or vertically, or will they always be separated by non-farmland (0) cells?
Should the output array be sorted based on the top-left corner coordinates of each farmland group? If so, what is the specific sorting criteria (e.g., row-major, column-major)?

Brute Force Solution

Approach

The brute force approach to finding farmland groups means we'll look at every single possible area within the entire farm. We check each potential area to see if it matches the definition of a 'farmland group'. After checking every possible area we return those that are a farmland group.

Here's how the algorithm would work step-by-step:

Start by considering the smallest possible area: a single piece of land.
Check if that piece of land is farmland (represented by a 1).
If it is farmland, see if it's the bottom-right part of a bigger farmland group. If it is, note that area.
Now, consider a bigger area: a two-by-two square of land.
Check if all the land in that square is farmland (all 1s).
If it is, see if it's the bottom-right section of a bigger group and note the group area if so.
Continue to check bigger and bigger areas - all possible sizes of rectangular areas of land within the farm.
Each time you find a rectangle of land that is completely farmland (all 1s) and is at the bottom-right part of a group, save it.
Once you have checked every possible area size and location within the farm, return the list of saved areas that met our 'farmland group' criteria.

Code Implementation

def find_farmland_brute_force(land):	rows = len(land)
	cols = len(land[0]) if rows > 0 else 0

	farmland_groups = []

	for start_row in range(rows):		for start_col in range(cols):			for end_row in range(start_row, rows):				for end_col in range(start_col, cols):					is_farmland_group = True

					# Check if all cells in the rectangle are farmland					for row_check in range(start_row, end_row + 1):						for col_check in range(start_col, end_col + 1):							if land[row_check][col_check] != 1:								is_farmland_group = False
								break
						if not is_farmland_group:							break

					if is_farmland_group:						#Confirm the rectangle is the bottom-right most group						is_bottom_right = True

						if end_row + 1 < rows:							for check_col in range(start_col, end_col + 1):								if land[end_row + 1][check_col] == 1:									is_bottom_right = False
									break

					if end_col + 1 < cols and is_bottom_right:						for check_row in range(start_row, end_row + 1):							if land[check_row][end_col + 1] == 1:								is_bottom_right = False
								break

					#Only save results if bottom right rectangle					if is_bottom_right:						farmland_groups.append([start_row, start_col, end_row, end_col])

	return farmland_groups

Big(O) Analysis

Time Complexity

O(m²n²) – The brute force approach iterates through all possible top-left and bottom-right corners within the farm, where m is the number of rows and n is the number of columns. This means we potentially iterate through all possible rectangles. For each rectangle defined by (row1, col1) and (row2, col2), we must verify that all the cells within that rectangle contain a '1'. The rectangle verification itself takes O((row2 - row1) * (col2 - col1)) time, which is O(mn) in the worst case. Considering the nested loops for defining the rectangle corners, the overall time complexity is O(m²n²).

Space Complexity

O(1) – The brute force approach, as described, only stores the coordinates of farmland groups (top-left and bottom-right). The number of such groups is independent of the total area of the farm. Since the algorithm only saves the identified farmland group coordinates, the extra space used consists of a list whose size depends on the number of farmland groups, not the total farm size. While the number of groups can vary, it's bounded by a factor independent of the input size N if we consider N to be rows * cols, hence the auxiliary space complexity is O(1).

Optimal Solution

Approach

We need to identify rectangular groups of farmland within a grid. The trick is to efficiently explore the grid, marking farmland as we find it to avoid revisiting the same area. We can achieve this by searching from the top-left corner, and growing rectangles as we discover connected farmland.

Here's how the algorithm would work step-by-step:

Go through each cell in the grid, row by row and column by column, starting from the top left.
If you find a cell that represents farmland, start exploring to find the complete rectangular area of that farmland.
To find the extent of the farmland, look rightwards and downwards until you hit a boundary of the farmland. This will give you the bottom-right corner of the rectangle.
Record the coordinates of the top-left and bottom-right corners of the rectangle.
Once you've found the entire rectangular area, mark all the farmland cells within it as 'visited' (or change their value) so you don't count them again in future steps.
Continue searching the grid, skipping over the visited farmland.
Repeat the process until you have identified all the farmland rectangles and recorded their top-left and bottom-right coordinates.

Code Implementation

def find_farmland(land_grid):
    rows = len(land_grid)
    cols = len(land_grid[0])
    farmland_groups = []

    for row_index in range(rows):
        for col_index in range(cols):
            if land_grid[row_index][col_index] == 1:
                # Found farmland, explore to find its boundaries.

                bottom_right_row = row_index
                bottom_right_col = col_index

                # Find the bottom right corner of the farmland rectangle.
                while bottom_right_row + 1 < rows and land_grid[bottom_right_row + 1][col_index] == 1:
                    bottom_right_row += 1

                while bottom_right_col + 1 < cols and land_grid[row_index][bottom_right_col + 1] == 1:
                    bottom_right_col += 1

                farmland_groups.append([row_index, col_index, bottom_right_row, bottom_right_col])

                # Mark the explored farmland as visited by changing its value.

                for i in range(row_index, bottom_right_row + 1):
                    for j in range(col_index, bottom_right_col + 1):
                        land_grid[i][j] = 0

    return farmland_groups

Big(O) Analysis

Time Complexity

O(m*n) – The primary driver of the time complexity is the nested loop that iterates through each cell of the grid (m rows and n columns). When farmland is encountered, we explore its rectangular extent. Marking farmland as visited ensures each cell is processed at most once. Therefore, the time complexity is proportional to the total number of cells in the grid, resulting in O(m*n).

Space Complexity

O(1) – The algorithm primarily iterates through the input grid in place. Although it marks visited cells, this is done directly within the input grid itself, thus not utilizing auxiliary space. No additional data structures that scale with the input size, such as lists or hash maps, are used. Therefore, the auxiliary space used remains constant regardless of the size of the input grid, resulting in O(1) space complexity.

Edge Cases

Case	How to Handle
Empty farmland array	Return an empty list since there's no farmland to group.
Single cell farmland array (1x1)	Return a list containing a single group with top-left and bottom-right coordinates being (0, 0).
All cells are farmland (all 1s)	Return a single group with top-left (0,0) and bottom-right (m-1, n-1) where m and n are dimensions.
No farmland cells (all 0s)	Return an empty list since there is no farmland.
Farmland forms multiple non-contiguous rectangles	The solution correctly identifies and returns each rectangle as a separate group using a traversal algorithm like DFS or BFS.
Farmland array is not rectangular (invalid input)	Throw an IllegalArgumentException if the input array is not rectangular.
Large farmland array (performance considerations)	Use iterative DFS or BFS instead of recursive approaches to avoid stack overflow errors and ensure reasonable time complexity.
Farmland contains only one large rectangle.	Correctly identify the top-left and bottom-right coordinates of the single large rectangle.

Empty farmland array

How to Handle:

Return an empty list since there's no farmland to group.

Single cell farmland array (1x1)

How to Handle:

Return a list containing a single group with top-left and bottom-right coordinates being (0, 0).

All cells are farmland (all 1s)

How to Handle:

Return a single group with top-left (0,0) and bottom-right (m-1, n-1) where m and n are dimensions.

No farmland cells (all 0s)

How to Handle:

Return an empty list since there is no farmland.

Farmland forms multiple non-contiguous rectangles

How to Handle:

The solution correctly identifies and returns each rectangle as a separate group using a traversal algorithm like DFS or BFS.

Farmland array is not rectangular (invalid input)

How to Handle:

Throw an IllegalArgumentException if the input array is not rectangular.

Large farmland array (performance considerations)

How to Handle:

Use iterative DFS or BFS instead of recursive approaches to avoid stack overflow errors and ensure reasonable time complexity.

Farmland contains only one large rectangle.

How to Handle:

Correctly identify the top-left and bottom-right coordinates of the single large rectangle.