Find Bottom Left Tree Value
Find Bottom Left Tree Value #2 Most Asked
MediumGiven the root of a binary tree, return the leftmost value in the last row of the tree.
Example 1:
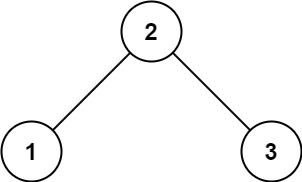
Input: root = [2,1,3] Output: 1
Example 2:
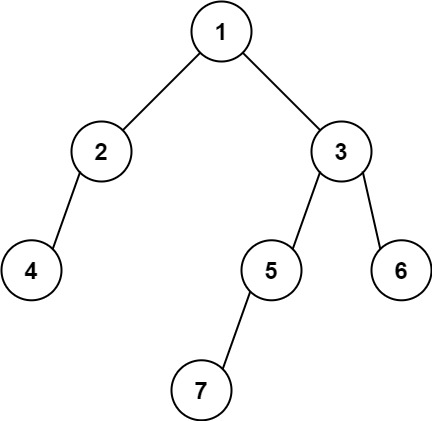
Input: root = [1,2,3,4,null,5,6,null,null,7] Output: 7
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -231 <= Node.val <= 231 - 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty, and if so, what should I return?
- What is the data type of the node values, and can they be negative?
- Is the input guaranteed to be a valid binary tree?
- If there are multiple nodes on the bottom left, which one should I return?
- Could you define what is considered the 'bottom left' node if the tree is not perfectly balanced?
Brute Force Solution
Approach
To find the bottom-left value in a tree, a brute-force approach involves exploring every single node. We essentially want to visit all the nodes and keep track of the leftmost node at the deepest level we've seen so far.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree.
- Explore every single path from the top all the way down to the bottom.
- As you go down each path, keep track of how deep you are.
- Also, when you reach a new depth, remember the leftmost node you encountered at that depth.
- Once you've explored every possible path, the node that you remembered as the leftmost at the deepest level is the answer.
Code Implementation
def find_bottom_left_tree_value(root):
deepest_level = -1
leftmost_value_at_deepest_level = 0
def depth_first_search(node, current_depth):
nonlocal deepest_level, leftmost_value_at_deepest_level
if node is None:
return
# If we've found a new deepest level
if current_depth > deepest_level:
deepest_level = current_depth
# Update the leftmost value at the deepest level
leftmost_value_at_deepest_level = node.val
# Explore left subtree first to find leftmost node
depth_first_search(node.left, current_depth + 1)
depth_first_search(node.right, current_depth + 1)
depth_first_search(root, 0)
return leftmost_value_at_deepest_levelBig(O) Analysis
Optimal Solution
Approach
To find the bottom-left value in a tree, we can use a breadth-first search approach, visiting nodes level by level. The leftmost node on the very last level we visit is the answer.
Here's how the algorithm would work step-by-step:
- Imagine exploring the tree level by level, like water spreading out evenly from the top.
- Start by looking at the very top node of the tree.
- Then look at all the nodes directly below it, from left to right.
- Continue moving down the tree, examining each level from left to right.
- Remember the very first node you see on the last level you visit. That's the bottom-left node.
- Once you reach a level with no nodes below it, the leftmost node of that level is your answer.
Code Implementation
def findBottomLeftValue(root):
queue = [root]
bottomLeftValue = 0
while queue:
levelLength = len(queue)
# Set to first value in level, this is most left one
bottomLeftValue = queue[0].val
for i in range(levelLength):
currentNode = queue.pop(0)
if currentNode.left:
queue.append(currentNode.left)
if currentNode.right:
queue.append(currentNode.right)
# The last most left value is the result
return bottomLeftValueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return null or a predefined value (e.g., -1) since there is no tree. |
| Tree with only one node (root) | Return the value of the root node immediately as it is both the leftmost and bottommost. |
| Complete binary tree of significant depth | BFS implementation guarantees the bottom level is reached efficiently; memory usage should be considered. |
| Highly unbalanced tree skewed to the right | BFS still functions correctly but might not be as efficient as for a balanced tree; consider if DFS could be more appropriate based on constraints. |
| Highly unbalanced tree skewed to the left | BFS will correctly identify the bottom left value. |
| Tree with duplicate node values | Duplicate node values do not affect the correctness of BFS or DFS as long as the leftmost node on the bottom level is correctly identified. |
| Tree with negative or zero node values | These values are valid node values and do not require special handling; the algorithm will process them as usual. |
| Integer overflow during node value comparison or storage | Ensure the data type used for node values and any intermediate calculations is large enough to prevent overflow; use long if necessary. |