Find Duplicate Subtrees
MediumGiven the root of a binary tree, return all duplicate subtrees.
For each kind of duplicate subtrees, you only need to return the root node of any one of them.
Two trees are duplicate if they have the same structure with the same node values.
Example 1:
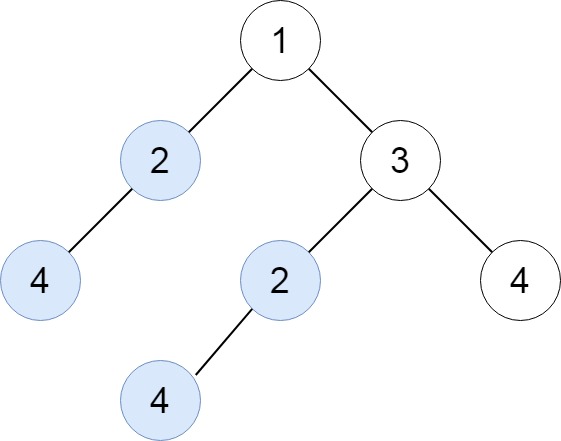
Input: root = [1,2,3,4,null,2,4,null,null,4] Output: [[2,4],[4]]
Example 2:
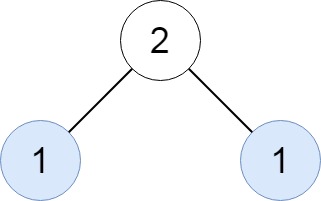
Input: root = [2,1,1] Output: [[1]]
Example 3:

Input: root = [2,2,2,3,null,3,null] Output: [[2,3],[3]]
Constraints:
- The number of the nodes in the tree will be in the range
[1, 5000] -200 <= Node.val <= 200
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node data within the tree?
- Can the tree be empty or contain only a single node?
- How should subtree equality be determined? Should the node values and the tree structure be identical for two subtrees to be considered duplicates?
- If multiple duplicate subtrees exist, should I return all of them, or just one representative subtree for each unique duplicate?
- What is the expected output format? Specifically, should I return the root nodes of the duplicate subtrees, or some other representation?
Brute Force Solution
Approach
We want to find all the trees within a larger tree that look exactly the same. The brute force method is like taking every possible subtree and comparing it to every other subtree to see if they match.
Here's how the algorithm would work step-by-step:
- First, consider every single part of the tree as a potential subtree.
- For each of these subtrees, create a description that captures its structure and the information it holds.
- Now, take the first subtree and compare its description to the description of every other subtree.
- If two subtrees have the exact same description, then we have found a duplicate.
- Repeat this comparison process for every subtree against all other subtrees.
- Keep a record of each unique duplicate subtree that you find to avoid reporting the same duplicate multiple times.
Code Implementation
def find_duplicate_subtrees_brute_force(root):
duplicate_subtrees = []
all_subtrees = []
def traverse(node):
if not node:
return
all_subtrees.append(node)
traverse(node.left)
traverse(node.right)
traverse(root)
def subtree_description(node):
if not node:
return "#"
return str(node.val) + "," + subtree_description(node.left) + "," + subtree_description(node.right)
for i in range(len(all_subtrees)):
for j in range(i + 1, len(all_subtrees)):
# Compare all possible subtrees.
if subtree_description(all_subtrees[i]) == subtree_description(all_subtrees[j]):
is_duplicate = False
# Check if we've already recorded the duplicate.
for previously_found in duplicate_subtrees:
if subtree_description(previously_found) == subtree_description(all_subtrees[i]):
is_duplicate = True
break
if not is_duplicate:
# Record the duplicate if it's a new one.
duplicate_subtrees.append(all_subtrees[i])
return duplicate_subtreesBig(O) Analysis
Optimal Solution
Approach
The efficient way to find duplicate subtrees is to represent each subtree as a unique string. We can then compare these strings to identify duplicates without traversing the entire tree multiple times. This avoids redundant checks and makes the process much faster.
Here's how the algorithm would work step-by-step:
- First, create a way to turn each subtree into a string representation. This string should capture the structure and data of the entire subtree.
- For any empty spot on the tree (like a missing branch), use a special marker in the string, so they are all consistently handled.
- Now, go through the entire tree, turning each subtree into its string form. Store each unique string we encounter.
- If we find a string that's already stored, that means we've found a duplicate subtree. Keep track of the root node of the duplicate subtree.
- In the end, report all the root nodes of the duplicate subtrees we've found.
Code Implementation
def find_duplicate_subtrees(root):
subtree_representation_map = {}
duplicate_subtrees = []
def get_subtree_string(node):
if not node:
return "#"
# Construct a unique string for the subtree.
subtree_string = str(node.val) + "," + get_subtree_string(node.left) + "," + get_subtree_string(node.right)
# Check if the subtree string already exists.
if subtree_string in subtree_representation_map:
subtree_representation_map[subtree_string] += 1
# Add the node to duplicates only once.
if subtree_representation_map[subtree_string] == 2:
# Mark this node as the root of a duplicate.
duplicate_subtrees.append(node)
else:
# Store the string if it's the first time.
subtree_representation_map[subtree_string] = 1
return subtree_string
get_subtree_string(root)
# Return all duplicate subtree root nodes.
return duplicate_subtreesBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree as input | Return an empty list immediately since there are no subtrees to compare. |
| A single-node tree | Return an empty list as a single node tree cannot have duplicate subtrees. |
| A tree where all nodes have the same value | The entire tree and all subtrees will be duplicates; ensure only the root of each distinct subtree structure is added to the result. |
| A tree where all nodes have distinct values | Return an empty list because no duplicate subtrees will exist. |
| Very large tree (potential stack overflow with recursion) | Consider using an iterative approach to traverse the tree instead of recursion, or increase stack size if using recursion. |
| Deeply skewed tree (e.g., a linked list) | This edge case tests the performance of the algorithm with imbalanced trees, potentially leading to worst-case time complexity; optimize the subtree comparison for such cases. |
| Trees with identical structure but different node values | The serialization/hashing method needs to incorporate node values to distinguish these trees. |
| Tree contains duplicate subtrees that are not direct children | The algorithm should identify all duplicate subtrees regardless of their level in the tree. |