Find Minimum Diameter After Merging Two Trees #11 Most Asked
HardThere exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.
You must connect one node from the first tree with another node from the second tree with an edge.
Return the minimum possible diameter of the resulting tree.
The diameter of a tree is the length of the longest path between any two nodes in the tree.
Example 1: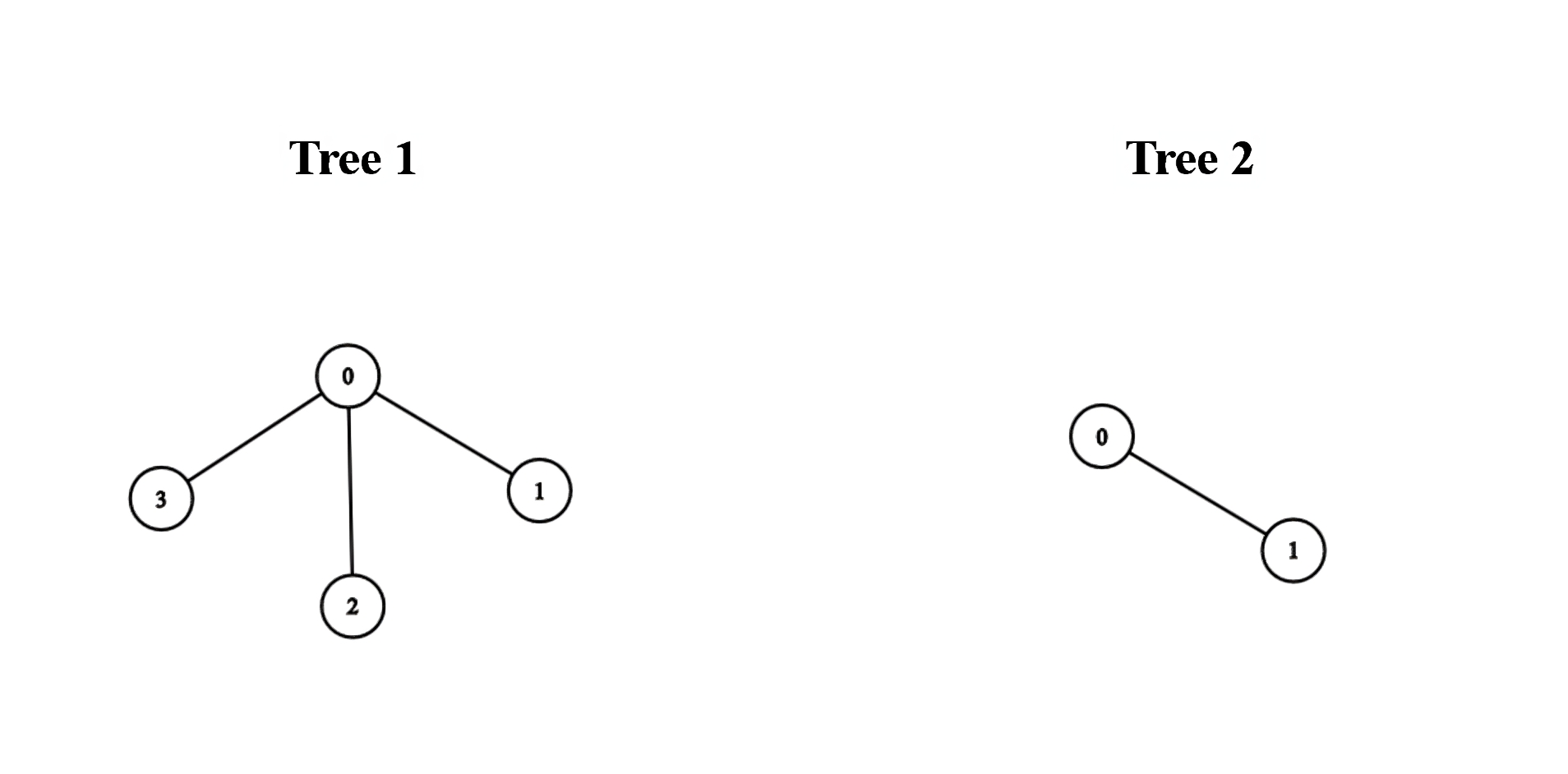
Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]
Output: 3
Explanation:
We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.
Example 2:
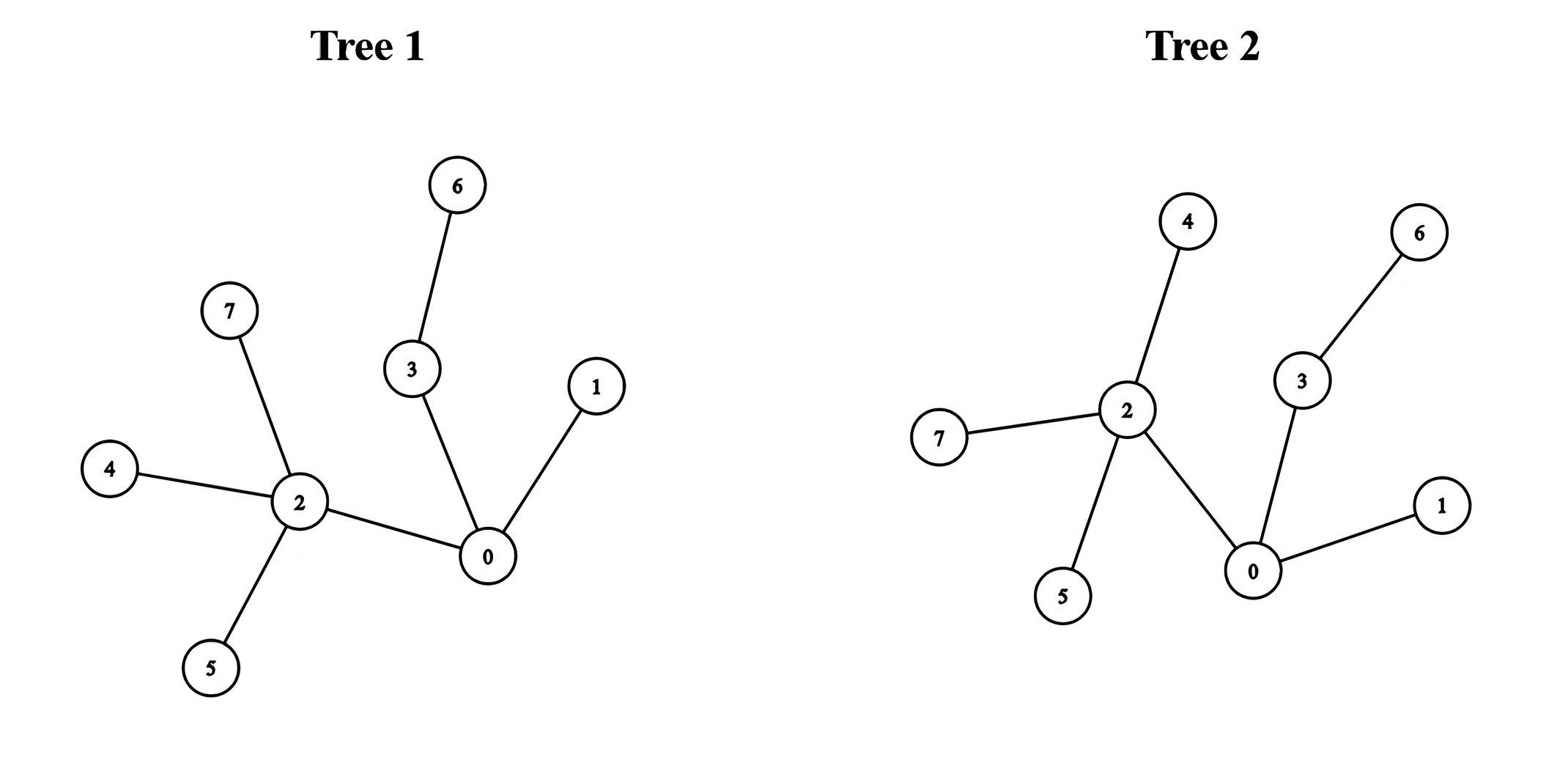
Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
Output: 5
Explanation:
We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.
Constraints:
1 <= n, m <= 105edges1.length == n - 1edges2.length == m - 1edges1[i].length == edges2[i].length == 2edges1[i] = [ai, bi]0 <= ai, bi < nedges2[i] = [ui, vi]0 <= ui, vi < m- The input is generated such that
edges1andedges2represent valid trees.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data structure used to represent the trees? Is it a custom tree node class, or can I assume it's something common like an adjacency list or dictionary?
- Can the trees be empty (i.e., null or contain no nodes)? What should I return in that case?
- Are the nodes' values relevant to the diameter calculation, or are we only concerned with the structure/connectivity of the trees?
- By 'merging,' do you mean connecting the two trees with a single edge between any two nodes in the respective trees? If so, am I allowed to choose the nodes for the connection?
- What is the range of possible node values or number of nodes in each tree?
Brute Force Solution
Approach
The brute force strategy explores every possible way to merge the two trees by connecting them at different pairs of nodes, one from each tree. For each possible merged tree, we calculate its diameter, and then we pick the smallest diameter among all the options. It's like trying every single connection and measuring each result to find the best one.
Here's how the algorithm would work step-by-step:
- Consider every single possible pair of nodes: one node from the first tree, and one node from the second tree.
- For each pair of nodes, temporarily connect them with a new edge, creating a new merged tree.
- Calculate the diameter of this newly created merged tree. The diameter is the longest path between any two nodes in the tree.
- Store the diameter you just calculated. Now, disconnect the two nodes you connected.
- Repeat these steps for every possible pair of nodes. This means you will create and measure the diameter of a lot of trees.
- Once you've tried every possible pair of nodes and have a list of all the diameters, find the smallest diameter from that list. That smallest diameter is the answer.
Code Implementation
class Node:
def __init__(self, value):
self.value = value
self.neighbors = []
def find_diameter_brute_force(tree1_nodes, tree2_nodes):
minimum_diameter = float('inf')
# Iterate through all possible node pairs
for first_tree_node in tree1_nodes:
for second_tree_node in tree2_nodes:
# Create a temporary edge between the nodes
first_tree_node.neighbors.append(second_tree_node)
second_tree_node.neighbors.append(first_tree_node)
# Calculate the diameter of the merged tree
diameter = calculate_diameter(tree1_nodes + tree2_nodes)
minimum_diameter = min(minimum_diameter, diameter)
# Remove the temporary edge
first_tree_node.neighbors.remove(second_tree_node)
second_tree_node.neighbors.remove(first_tree_node)
return minimum_diameter
def calculate_diameter(all_nodes):
max_diameter = 0
# Find the diameter by exploring every pair of nodes
for start_node in all_nodes:
for end_node in all_nodes:
if start_node != end_node:
# Calculate path length using bfs
path_length = bfs(start_node, end_node)
max_diameter = max(max_diameter, path_length)
return max_diameter
def bfs(start_node, end_node):
queue = [(start_node, 0)]
visited = {start_node}
while queue:
current_node, distance = queue.pop(0)
if current_node == end_node:
return distance
for neighbor in current_node.neighbors:
if neighbor not in visited:
visited.add(neighbor)
queue.append((neighbor, distance + 1))
return float('inf') # if no path exists, return infinity.Big(O) Analysis
Optimal Solution
Approach
To find the smallest possible diameter after combining two trees, we need to be smart about how we connect them. The trick is to join the trees in a way that minimizes the longest path, by finding the longest paths within each tree individually, and then connecting them strategically.
Here's how the algorithm would work step-by-step:
- First, find the longest path (diameter) in each of the two trees separately. Think of this as measuring the longest distance across each tree.
- Also, for each tree, find the furthest point from the middle of its longest path. This is essentially finding the radius of each tree if we consider the diameter as the central line.
- Now, connect the two trees. The smartest way to do this is to connect the furthest points found in the previous step. By connecting these points, we're essentially linking the two trees as close to their 'centers' as possible relative to their individual diameters.
- Finally, calculate the diameter of the new combined tree. The diameter will be the longest of three possible paths: the diameter of the first tree, the diameter of the second tree, or a path that goes from one end of the first tree's diameter, through the connection, to the other end of the second tree's diameter.
Code Implementation
def find_minimum_diameter_after_merging(
tree1_edges, tree2_edges):
def get_diameter_and_furthest_node(edges):
number_of_nodes = 0
for edge in edges:
number_of_nodes = max(number_of_nodes, edge[0], edge[1])
number_of_nodes += 1
graph = [[] for _ in range(number_of_nodes)]
for edge in edges:
node1, node2 = edge
graph[node1].append(node2)
graph[node2].append(node1)
def bfs(start_node):
distances = [-1] * number_of_nodes
distances[start_node] = 0
queue = [start_node]
farthest_node = start_node
while queue:
current_node = queue.pop(0)
for neighbor in graph[current_node]:
if distances[neighbor] == -1:
distances[neighbor] = distances[current_node] + 1
queue.append(neighbor)
farthest_node = neighbor
return farthest_node, distances
# Find one end of the diameter
farthest_node_1, _ = bfs(0)
# Find the other end of the diameter and distances from farthest_node_1
farthest_node_2, distances = bfs(farthest_node_1)
diameter = distances[farthest_node_2]
# Find the middle of the diameter and the maximum distance to it
middle_node = farthest_node_2
max_distance_from_middle = 0
for node in range(number_of_nodes):
distance1 = min(distances[node],
distances[farthest_node_2] - distances[node])
max_distance_from_middle = max(
max_distance_from_middle, distances[node])
return diameter, farthest_node_1
# Calculate the diameter and furthest node for each tree
diameter1, furthest_node1 = get_diameter_and_furthest_node(tree1_edges)
diameter2, furthest_node2 = get_diameter_and_furthest_node(tree2_edges)
# Connect the two trees using the furthest nodes
# This merges them at points near the center of each longest path.
new_edges = tree1_edges + tree2_edges + [(furthest_node1, furthest_node2)]
# Calculate the new diameter using the combined graph
new_diameter, _ = get_diameter_and_furthest_node(new_edges)
return new_diameterBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both trees are empty (null) | Return 0 as the minimum diameter if both input trees are empty, indicating no path exists. |
| One tree is empty (null), the other is not | Return the diameter of the non-empty tree, as there's nothing to merge with. |
| Trees with single nodes | Merge the two single nodes by creating an edge between them, resulting in a diameter of 1. |
| Trees with only two nodes each | Consider all possible connections between the two trees to find the minimum diameter after merging. |
| Trees with a very large number of nodes (potential stack overflow with recursion) | Employ iterative BFS or DFS to calculate tree diameters, preventing stack overflow issues for large trees. |
| One tree is a single long chain, the other is a star graph. | Connecting the center of the star graph to the middle of the chain can produce optimal results; explore various connection points to minimize diameter. |
| Trees where all nodes have the same value | The actual node values do not matter for diameter calculation, only the structure and connections in the trees. |
| Disconnected graphs passed as trees (cycles present) | The input is technically invalid if it contains cycles; the algorithm should assume that input is always valid tree, otherwise additional cycle detection logic might be needed, returning an error message to signal the problem. |