Find Mode in Binary Search Tree
EasyGiven the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.
If the tree has more than one mode, return them in any order.
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than or equal to the node's key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
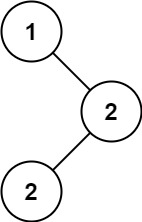
Input: root = [1,null,2,2] Output: [2]
Example 2:
Input: root = [0] Output: [0]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -105 <= Node.val <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the BST can hold? Can they be negative, zero, or floating-point numbers?
- What should I return if the BST is empty or contains only one node?
- If there are multiple modes (i.e., multiple values appearing with the same maximum frequency), should I return all of them? In what order?
- Are there any constraints on the structure of the BST? Is it guaranteed to be balanced or nearly balanced?
- Could there be duplicate values within the tree, and if so, how should I handle them when calculating the mode?
Brute Force Solution
Approach
The brute force method to find the mode in a Binary Search Tree involves checking every value in the tree. We will count how many times each value appears, and then identify the value or values that appear most frequently.
Here's how the algorithm would work step-by-step:
- Go through the entire tree and make a list of all the unique values that appear.
- For each unique value, revisit the entire tree and count how many times that specific value appears.
- Keep track of the count for each unique value.
- Once you have counted the occurrences of every unique value, find the highest count.
- The value or values that have this highest count are the mode(s) of the tree.
Code Implementation
def find_mode_brute_force(root):
unique_values = []
value_counts = {}
def traverse_tree(node):
if node:
if node.val not in unique_values:
unique_values.append(node.val)
traverse_tree(node.left)
traverse_tree(node.right)
traverse_tree(root)
# Iterate through each unique value
for unique_value in unique_values:
value_counts[unique_value] = 0
def count_value(node, value_to_count):
if node:
if node.val == value_to_count:
value_counts[value_to_count] += 1
count_value(node.left, value_to_count)
count_value(node.right, value_to_count)
# For each unique value, count occurrences
count_value(root, unique_value)
max_count = 0
# Find the maximum count
for unique_value in unique_values:
if value_counts[unique_value] > max_count:
max_count = value_counts[unique_value]
modes = []
# Collect the modes based on the maximum count
for unique_value in unique_values:
if value_counts[unique_value] == max_count:
modes.append(unique_value)
# Return the list of modes
return modesBig(O) Analysis
Optimal Solution
Approach
To efficiently find the most frequent value (the mode) in a binary search tree, we take advantage of the tree's sorted nature. We'll traverse the tree in a specific order, keeping track of the current value and its frequency, then updating our mode whenever we encounter a new, higher frequency.
Here's how the algorithm would work step-by-step:
- Go through the tree in a specific order, visiting the left side, then the current node, then the right side for each part of the tree. This way, we visit the nodes in sorted order.
- Keep track of the number we just saw and how many times in a row we've seen that exact same number.
- If the current number is the same as the previous one, increase the count.
- If the current number is different, reset the count to 1 and remember the current number.
- During the entire process, keep track of the highest count seen so far.
- If we see a count that is higher than the highest count recorded, forget the previous mode(s) and only remember the current number. It is now the only mode.
- If we see a count that is equal to the highest count recorded, then the current number is also a mode.
- Once we've visited every number in the tree, we'll know all the numbers that appear the most often and return them.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def findMode(root):
modes = []
max_frequency = 0
current_frequency = 0
previous_value = None
def inorder_traversal(node):
nonlocal modes, max_frequency, current_frequency, previous_value
if not node:
return
inorder_traversal(node.left)
current_value = node.val
if current_value == previous_value:
current_frequency += 1
else:
current_frequency = 1
# Check if current value is a mode.
if current_frequency > max_frequency:
# Reset modes if current frequency is higher.
modes = [current_value]
max_frequency = current_frequency
elif current_frequency == max_frequency:
# Add current value as a mode.
modes.append(current_value)
previous_value = current_value
inorder_traversal(node.right)
inorder_traversal(root)
return modesBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty tree (null root) | Return an empty list if the root is null, as there are no nodes and thus no mode. |
| Tree with only one node | Return a list containing the value of the single node in the tree. |
| Tree where all nodes have the same value | The algorithm should correctly identify the single value as the mode, and return a list containing only that value. |
| Tree with multiple modes (same frequency) | The algorithm should correctly identify and return all modes in a list. |
| Skewed tree (e.g., all nodes on the left) | Iterative inorder traversal avoids stack overflow issues that could arise with recursive approaches on highly skewed trees. |
| Large BST (scalability concerns) | Inorder traversal has O(n) time complexity and avoids excessive memory usage by not storing entire tree in memory. |
| Tree with negative values | The mode finding logic should function correctly with negative values as the comparison is based on frequency counts, not value ranges. |
| Integer overflow in count | Use appropriate data type (e.g., long) for storing frequency counts to prevent overflow issues with very large trees and high frequency nodes. |