Find the City With the Smallest Number of Neighbors at a Threshold Distance

Medium

Asked by:

52 views

Topics:

GraphsDynamic Programming

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [from_i, to_i, weight_i] represents a bidirectional and weighted edge between cities from_i and to_i, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example 1:

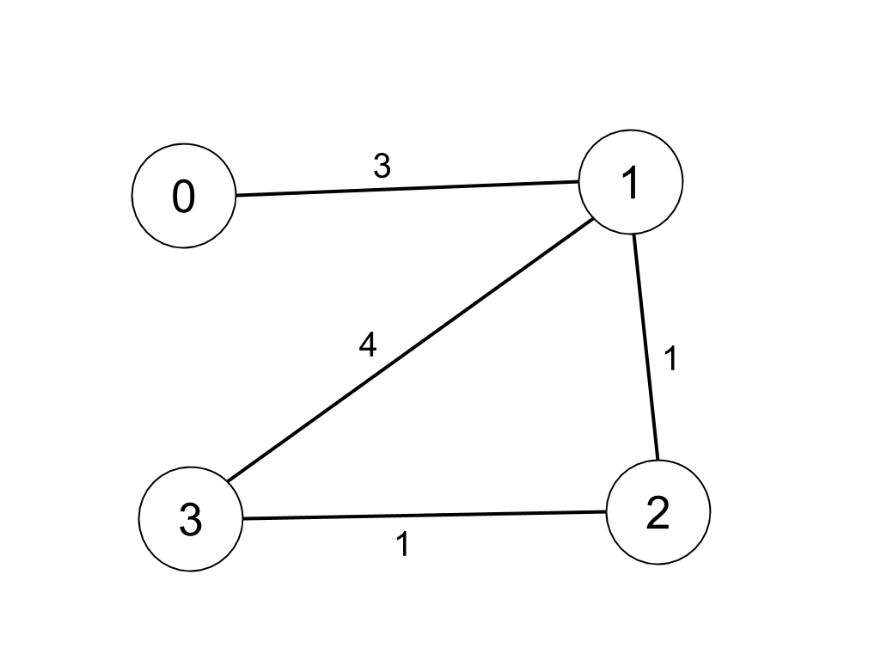
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

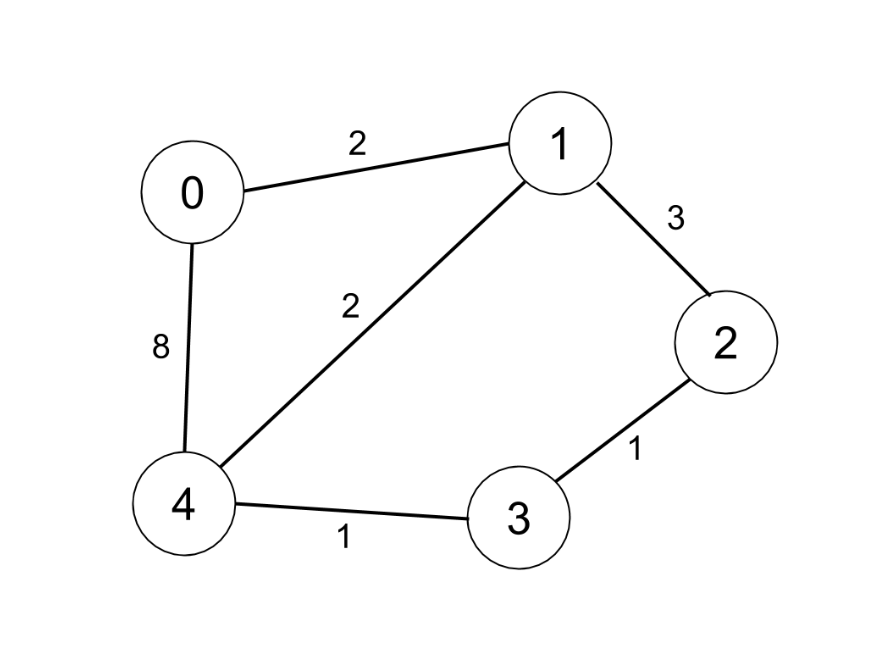
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2.

Constraints:

2 <= n <= 100
1 <= edges.length <= n * (n - 1) / 2
edges[i].length == 3
0 <= from_i < to_i < n
1 <= weight_i, distanceThreshold <= 10^4
All pairs (from_i, to_i) are distinct.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible ranges for the number of cities `n` and the threshold distance?
Are the edge weights in the `edges` list guaranteed to be non-negative?
If multiple cities have the same smallest number of reachable neighbors within the threshold, which one should I return (e.g., the city with the smallest index)?
Is the graph guaranteed to be connected, or could there be disconnected components?
If no city has any reachable neighbors within the threshold distance, what value should I return?

Brute Force Solution

Approach

The brute force approach here is like checking every single city to see which one has the fewest reachable neighbors within a certain distance. We will look at each city one by one and figure out how many other cities are close enough.

Here's how the algorithm would work step-by-step:

Pick a city. Let's call it the starting city.
For that starting city, look at all the other cities in the entire map.
For each of those other cities, figure out the distance between the starting city and that other city.
If that distance is short enough (less than or equal to our threshold distance), count that other city as a reachable neighbor from our starting city.
Repeat steps two through four for all the other cities, so we know exactly how many reachable neighbors the starting city has.
Remember how many reachable neighbors the starting city has.
Now, pick a different city and repeat steps one through six to find out how many reachable neighbors that city has.
Keep doing this for every single city on the map.
Once we have the number of reachable neighbors for every city, compare all the numbers we have collected.
Find the city with the smallest number of reachable neighbors. If there is a tie, choose the city with the highest number.

Code Implementation

def find_the_city(
    number_of_cities, edges, distance_threshold
):
    smallest_number_reachable_cities = number_of_cities
    city_with_smallest_number_reachable_cities = -1

    for starting_city in range(number_of_cities):
        number_reachable_cities = 0

        for other_city in range(number_of_cities):
            if starting_city == other_city:
                continue

            distance = find_distance(
                starting_city, other_city, number_of_cities, edges
            )

            # Count if the other city is reachable from the starting city
            if distance <= distance_threshold:
                number_reachable_cities += 1

        # Update city if smaller neighbor count or tie with larger city
        if (
            number_reachable_cities
            < smallest_number_reachable_cities
        ):
            smallest_number_reachable_cities = number_reachable_cities
            city_with_smallest_number_reachable_cities = starting_city

        elif (
            number_reachable_cities
            == smallest_number_reachable_cities
        ):
            city_with_smallest_number_reachable_cities = max(
                city_with_smallest_number_reachable_cities,
                starting_city,
            )

    return city_with_smallest_number_reachable_cities

def find_distance(city1, city2, number_of_cities, edges):
    distances = [
        [float('inf')] * number_of_cities for _ in range(number_of_cities)
    ]

    for i in range(number_of_cities):
        distances[i][i] = 0

    for edge in edges:
        city_a, city_b, weight = edge
        distances[city_a][city_b] = weight
        distances[city_b][city_a] = weight

    # Floyd-Warshall algorithm to find shortest paths
    for intermediate_city in range(number_of_cities):
        for i in range(number_of_cities):
            for j in range(number_of_cities):
                distances[i][j] = min(
                    distances[i][j],
                    distances[i][intermediate_city]
                    + distances[intermediate_city][j],
                )

    return distances[city1][city2]

Big(O) Analysis

Time Complexity

O(n*n*m) – The algorithm iterates through each of the n cities as a starting city. For each starting city, it iterates through all the other n cities to calculate the distance. The distance calculation requires iterating through m roads/edges to discover if the other city is reachable within the threshold distance. Therefore the overall complexity is approximately n * n * m, which simplifies to O(n*n*m).

Space Complexity

O(1) – The brute force approach, as described, primarily involves iterating and comparing values. While we store the count of reachable neighbors for each starting city, we only need to keep track of the minimum count found so far and the corresponding city with that minimum count. Therefore, the auxiliary space used remains constant irrespective of the number of cities (N) or roads, resulting in O(1) space complexity.

Optimal Solution

Approach

The problem asks to find a city with the fewest reachable cities within a certain distance. Instead of calculating distances repeatedly, the most efficient approach leverages a well-known algorithm to pre-compute all pairwise distances between cities, then quickly counts the reachable cities for each city.

Here's how the algorithm would work step-by-step:

First, use a standard algorithm to calculate the shortest path between every pair of cities. This algorithm efficiently finds the shortest distance between all pairs in one go. Consider this as creating a distance chart between all cities.
Next, for each city, go through the distance chart and count how many other cities are within the specified distance threshold from that city. Essentially count how many cities are 'close enough'.
Keep track of which city has the smallest count of 'close enough' neighbors. If multiple cities have the same smallest count, choose the one with the highest city number.
Finally, return the city with the smallest number of neighbors within the threshold distance.

Code Implementation

def find_the_city(number_of_cities, edges, distance_threshold):
    distance_matrix = [[float('inf')] * number_of_cities for _ in range(number_of_cities)]

    for i in range(number_of_cities):
        distance_matrix[i][i] = 0

    for start_node, end_node, weight in edges:
        distance_matrix[start_node][end_node] = weight
        distance_matrix[end_node][start_node] = weight

    # Floyd-Warshall Algorithm to calculate all-pairs shortest paths.
    for intermediate_node in range(number_of_cities):
        for start_node in range(number_of_cities):
            for end_node in range(number_of_cities):
                distance_matrix[start_node][end_node] = min(
                    distance_matrix[start_node][end_node],
                    distance_matrix[start_node][intermediate_node] + distance_matrix[intermediate_node][end_node]
                )

    smallest_number_of_reachable_cities = number_of_cities
    city_with_smallest_number_of_reachable_cities = -1

    # Iterate through each city to find the one with the smallest number of reachable cities.
    for current_city in range(number_of_cities):
        number_of_reachable_cities = 0

        for other_city in range(number_of_cities):
            if distance_matrix[current_city][other_city] <= distance_threshold:
                number_of_reachable_cities += 1

        # Track the city with the fewest reachable cities.
        if number_of_reachable_cities <= smallest_number_of_reachable_cities:

            # Break ties by selecting the city with the highest index.
            if number_of_reachable_cities < smallest_number_of_reachable_cities:
                smallest_number_of_reachable_cities = number_of_reachable_cities
                city_with_smallest_number_of_reachable_cities = current_city
            else:
                city_with_smallest_number_of_reachable_cities = current_city

    return city_with_smallest_number_of_reachable_cities

Big(O) Analysis

Time Complexity

O(n^3) – The algorithm first computes all-pairs shortest paths, which, using the Floyd-Warshall algorithm (a common choice), takes O(n^3) time, where n is the number of cities. Then, for each of the n cities, it iterates through all other cities (n iterations) to count neighbors within the threshold. This neighbor counting step takes O(n^2) time. Since O(n^3) dominates O(n^2), the overall time complexity is O(n^3).

Space Complexity

O(N^2) – The algorithm first calculates the shortest path between every pair of cities, requiring a matrix to store these distances. This matrix, representing the distance chart between all cities, has dimensions N x N, where N is the number of cities. Therefore, the auxiliary space is dominated by this N x N matrix. Other variables used for counting neighbors or tracking the best city require constant space, so the overall auxiliary space complexity is O(N^2).

Edge Cases

Case	How to Handle
Empty graph (n = 0 or edges is empty)	Return 0, as the problem states to return a city even if no connections exist.
Single node graph (n = 1, edges is empty)	Return 0, as it's the only city and has no neighbors.
Threshold distance is zero.	Only cities connected directly to themselves (if such edges exist) will be counted as neighbors, otherwise none.
All edge weights are greater than the threshold.	Every city will have zero reachable cities within the threshold distance.
Complete graph with all edge weights equal to 1 and threshold < 1.	No cities will be reachable, return the city with the smallest index (n-1).
Graph with disconnected components.	The algorithm must correctly compute the number of reachable nodes within the threshold for each component separately.
Large graph (n approaching constraints) to test performance	Floyd-Warshall algorithm or Dijkstra with priority queue are preferred for efficiency.
Integer overflow in distance calculations when edge weights or threshold are large.	Use long data type to store intermediate distances to avoid potential overflow.

Empty graph (n = 0 or edges is empty)

How to Handle:

Return 0, as the problem states to return a city even if no connections exist.

Single node graph (n = 1, edges is empty)

How to Handle:

Return 0, as it's the only city and has no neighbors.

Threshold distance is zero.

How to Handle:

Only cities connected directly to themselves (if such edges exist) will be counted as neighbors, otherwise none.

All edge weights are greater than the threshold.

How to Handle:

Every city will have zero reachable cities within the threshold distance.

Complete graph with all edge weights equal to 1 and threshold < 1.

How to Handle:

No cities will be reachable, return the city with the smallest index (n-1).

Graph with disconnected components.

How to Handle:

The algorithm must correctly compute the number of reachable nodes within the threshold for each component separately.

Large graph (n approaching constraints) to test performance

How to Handle:

Floyd-Warshall algorithm or Dijkstra with priority queue are preferred for efficiency.

Integer overflow in distance calculations when edge weights or threshold are large.

How to Handle:

Use long data type to store intermediate distances to avoid potential overflow.