Find the Maximum Number of Fruits Collected

Hard

Asked by:

2 views

Topics:

ArraysDynamic Programming

There is a game dungeon comprised of n x n rooms arranged in a grid.

You are given a 2D array fruits of size n x n, where fruits[i][j] represents the number of fruits in the room (i, j). Three children will play in the game dungeon, with initial positions at the corner rooms (0, 0), (0, n - 1), and (n - 1, 0).

The children will make exactly n - 1 moves according to the following rules to reach the room (n - 1, n - 1):

The child starting from (0, 0) must move from their current room (i, j) to one of the rooms (i + 1, j + 1), (i + 1, j), and (i, j + 1) if the target room exists.
The child starting from (0, n - 1) must move from their current room (i, j) to one of the rooms (i + 1, j - 1), (i + 1, j), and (i + 1, j + 1) if the target room exists.
The child starting from (n - 1, 0) must move from their current room (i, j) to one of the rooms (i - 1, j + 1), (i, j + 1), and (i + 1, j + 1) if the target room exists.

When a child enters a room, they will collect all the fruits there. If two or more children enter the same room, only one child will collect the fruits, and the room will be emptied after they leave.

Return the maximum number of fruits the children can collect from the dungeon.

Example 1:

Input: fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]

Output: 100

Explanation:

In this example:

The 1^st child (green) moves on the path (0,0) -> (1,1) -> (2,2) -> (3, 3).
The 2^nd child (red) moves on the path (0,3) -> (1,2) -> (2,3) -> (3, 3).
The 3^rd child (blue) moves on the path (3,0) -> (3,1) -> (3,2) -> (3, 3).

In total they collect 1 + 6 + 11 + 16 + 4 + 8 + 12 + 13 + 14 + 15 = 100 fruits.

Example 2:

Input: fruits = [[1,1],[1,1]]

Output: 4

Explanation:

In this example:

The 1^st child moves on the path (0,0) -> (1,1).
The 2^nd child moves on the path (0,1) -> (1,1).
The 3^rd child moves on the path (1,0) -> (1,1).

In total they collect 1 + 1 + 1 + 1 = 4 fruits.

Constraints:

2 <= n == fruits.length == fruits[i].length <= 1000
0 <= fruits[i][j] <= 1000

Find the Maximum Number of Fruits Collected

Hard

Asked by:

2 views

Topics:

ArraysDynamic Programming

There is a game dungeon comprised of n x n rooms arranged in a grid.

You are given a 2D array fruits of size n x n, where fruits[i][j] represents the number of fruits in the room (i, j). Three children will play in the game dungeon, with initial positions at the corner rooms (0, 0), (0, n - 1), and (n - 1, 0).

The children will make exactly n - 1 moves according to the following rules to reach the room (n - 1, n - 1):

The child starting from (0, 0) must move from their current room (i, j) to one of the rooms (i + 1, j + 1), (i + 1, j), and (i, j + 1) if the target room exists.
The child starting from (0, n - 1) must move from their current room (i, j) to one of the rooms (i + 1, j - 1), (i + 1, j), and (i + 1, j + 1) if the target room exists.
The child starting from (n - 1, 0) must move from their current room (i, j) to one of the rooms (i - 1, j + 1), (i, j + 1), and (i + 1, j + 1) if the target room exists.

When a child enters a room, they will collect all the fruits there. If two or more children enter the same room, only one child will collect the fruits, and the room will be emptied after they leave.

Return the maximum number of fruits the children can collect from the dungeon.

Example 1:

Input: fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]

Output: 100

Explanation:

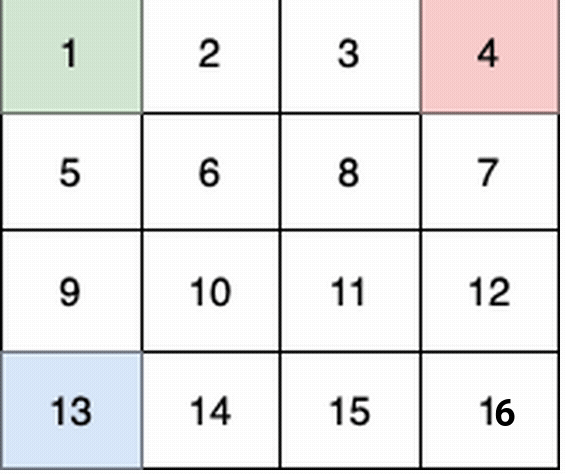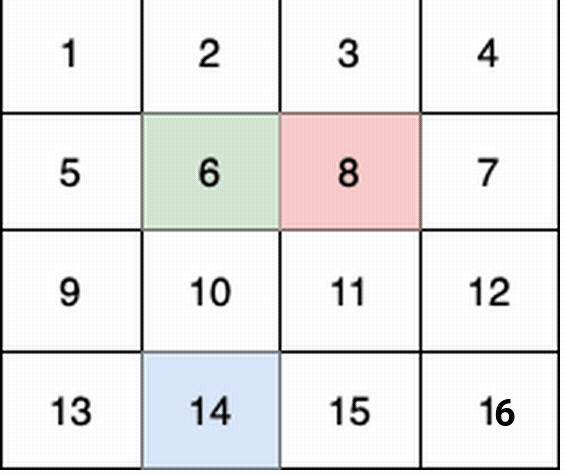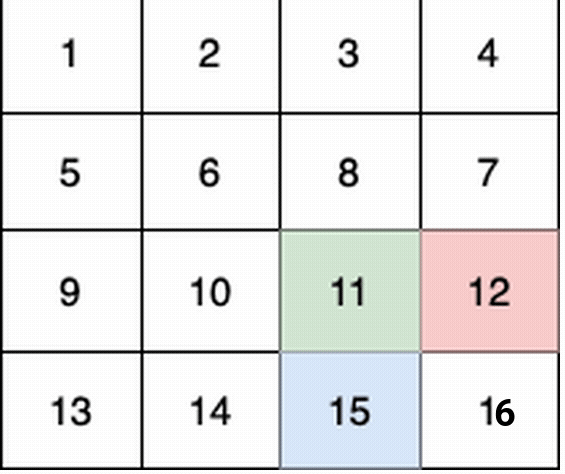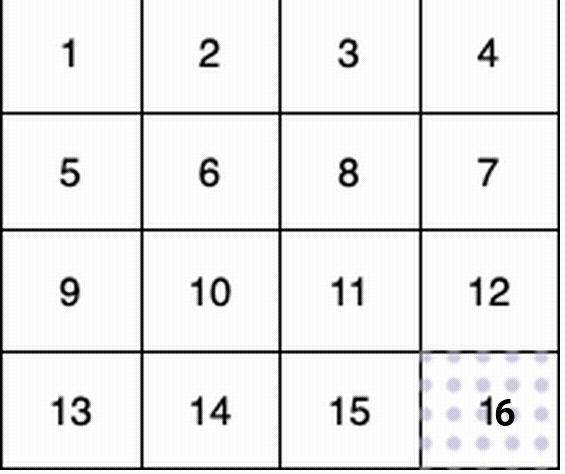
In this example:

The 1^st child (green) moves on the path (0,0) -> (1,1) -> (2,2) -> (3, 3).
The 2^nd child (red) moves on the path (0,3) -> (1,2) -> (2,3) -> (3, 3).
The 3^rd child (blue) moves on the path (3,0) -> (3,1) -> (3,2) -> (3, 3).

In total they collect 1 + 6 + 11 + 16 + 4 + 8 + 12 + 13 + 14 + 15 = 100 fruits.

Example 2:

Input: fruits = [[1,1],[1,1]]

Output: 4

Explanation:

In this example:

The 1^st child moves on the path (0,0) -> (1,1).
The 2^nd child moves on the path (0,1) -> (1,1).
The 3^rd child moves on the path (1,0) -> (1,1).

In total they collect 1 + 1 + 1 + 1 = 4 fruits.

Constraints:

2 <= n == fruits.length == fruits[i].length <= 1000
0 <= fruits[i][j] <= 1000

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values for the integers in the `fruits` array?
Can `k` be zero? What should the function return if the `fruits` array is empty?
Are the fruits represented by non-negative integers only, or can negative values be present?
If no sequence of trees allows collecting fruits with at most `k` distinct types, what should be returned?
Is `k` guaranteed to be less than or equal to the number of unique fruit types in the `fruits` array?

Brute Force Solution

Approach

We want to find the most fruits we can pick while moving along a row of fruit trees. The brute force strategy involves considering every possible section of trees we could pick from to see which one gives us the most fruit.

Here's how the algorithm would work step-by-step:

Start by considering just the first tree.
Then, look at the first two trees, then the first three, and so on, each time counting the total number of fruits.
After that, start at the second tree and consider just that tree, then the second and third, then the second, third, and fourth, and so on, again counting the fruits each time.
Continue this process, starting at each tree in the row, and considering all possible consecutive sections of trees.
As you calculate the total fruit for each section, keep track of the largest total you've seen so far.
Once you've checked every possible section of trees, the largest total you recorded is the maximum number of fruits you can collect.

Code Implementation

def find_max_fruits_collected_brute_force(fruit_tree_row):
    maximum_fruits_collected = 0

    # Iterate through all possible starting trees
    for start_tree_index in range(len(fruit_tree_row)):

        current_fruits_collected = 0

        # Iterate through all possible ending trees from the starting tree
        for end_tree_index in range(start_tree_index, len(fruit_tree_row)):

            current_fruits_collected += fruit_tree_row[end_tree_index]

            # Update the maximum fruits collected if the current section is better
            maximum_fruits_collected = max(maximum_fruits_collected, current_fruits_collected)

    return maximum_fruits_collected

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – The brute force approach iterates through all possible subarrays of the input array of size n. The outer loop iterates n times, determining the starting index of the subarray. The inner loop iterates up to n times, calculating the sum of the elements within that subarray. Therefore, the number of operations is proportional to the sum of integers from 1 to n, which is n*(n+1)/2. This simplifies to O(n²).

Space Complexity

O(1) – The provided brute force approach primarily involves iterating through all possible subarrays and keeping track of the maximum fruit count. No auxiliary data structures that scale with the input size N (number of trees) are used. The algorithm only stores a few integer variables, such as loop counters and a variable to store the maximum fruit count seen so far. Therefore, the auxiliary space used is constant, regardless of the number of trees.

Optimal Solution

Approach

Imagine you're a fruit picker who can only carry two types of fruit at once. The goal is to walk along a row of fruit trees and collect the most fruit possible while sticking to this two-type limit. We'll use a clever method to keep track of the longest possible walk while always following the rules.

Here's how the algorithm would work step-by-step:

Start walking along the row of fruit trees.
Keep track of the last two types of fruit you've picked and the quantity of each fruit.
As you walk, if you encounter a new type of fruit (a third kind), stop walking and calculate how many total fruits you've collected since the last time you saw one of the two fruits you had been carrying.
Record the length of the fruits you picked until you encountered a third kind of fruit.
Slide over to the right of the last of the type of the old fruits you were picking and continue walking, tracking the types of fruits as you did previously.
Keep repeating this process until you reach the end of the row of fruit trees.
Finally, compare all of the lengths that you recorded and return the largest length; this is the most fruit you could have picked while only ever carrying two types of fruit.

Code Implementation

def find_max_fruits_collected(fruits):
    max_fruits_collected = 0
    window_start = 0
    fruit_frequency = {}

    for window_end in range(len(fruits)):
        right_fruit = fruits[window_end]
        if right_fruit not in fruit_frequency:
            fruit_frequency[right_fruit] = 0
        fruit_frequency[right_fruit] += 1

        # Shrink the sliding window until we have at most 2 fruit types
        while len(fruit_frequency) > 2:
            left_fruit = fruits[window_start]
            fruit_frequency[left_fruit] -= 1

            if fruit_frequency[left_fruit] == 0:
                del fruit_frequency[left_fruit]

            window_start += 1

        # Update the maximum fruits collected
        max_fruits_collected = max(max_fruits_collected, window_end - window_start + 1)

    return max_fruits_collected

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through the array of fruit trees using a sliding window approach. In the worst-case scenario, the window might expand to cover the entire array as we attempt to maximize the number of fruits collected while adhering to the two-fruit-type constraint. We visit each tree a maximum of once or twice, resulting in a time complexity proportional to the number of trees (n). Therefore, the time complexity is O(n).

Space Complexity

O(1) – The algorithm keeps track of the last two types of fruits and their quantities. This requires storing a constant number of variables (at most two fruit types and their counts). Therefore, the auxiliary space used does not depend on the input size N (number of fruit trees) and remains constant.

Edge Cases

Case	How to Handle
Empty fruits array	Return 0 if the input array is empty since no fruits can be collected.
Fruits array with one element	Return the value of the single element if k >= 1 since one fruit type is allowed.
k is zero	Return 0 if k is zero since no distinct fruit types are allowed.
Fruits array contains only one type of fruit	Return the length of the array as all fruits can be collected since only one fruit type exists.
k is larger than the number of distinct fruit types in the array	Return the length of the array since all fruits can be collected as we are allowed to pick more fruit types than are available.
Fruits array with a very long sequence of the same fruit type followed by a different type	The sliding window approach correctly handles this by expanding the window to include the different type and then contracting if the number of distinct types exceeds k.
Fruits array contains large numbers potentially leading to integer overflow if summing	The algorithm focuses on counting distinct fruit types and tracking the length of the subarray, so it doesn't require summing potentially large fruit counts.
All fruits are distinct and k = 1	Return 1, because the sliding window will start with one element and will never expand since having 2 distinct fruit types breaks the constraint.