Find the Maximum Sum of Node Values #2 Most Asked

Hard

1 view

Topics:

Dynamic ProgrammingGreedy AlgorithmsTreesGraphsBit Manipulation

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 0-indexed 2D integer array edges of length n - 1, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i in the tree. You are also given a positive integer k, and a 0-indexed array of non-negative integers nums of length n, where nums[i] represents the value of the node numbered i.

Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:

Choose any edge [u, v] connecting the nodes u and v, and update their values as follows:
- nums[u] = nums[u] XOR k
- nums[v] = nums[v] XOR k

Return the maximum possible sum of the values Alice can achieve by performing the operation any number of times.

Example 1:

Input: nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
Output: 6
Explanation: Alice can achieve the maximum sum of 6 using a single operation:
- Choose the edge [0,2]. nums[0] and nums[2] become: 1 XOR 3 = 2, and the array nums becomes: [1,2,1] -> [2,2,2].
The total sum of values is 2 + 2 + 2 = 6.
It can be shown that 6 is the maximum achievable sum of values.

Example 2:

Input: nums = [2,3], k = 7, edges = [[0,1]]
Output: 9
Explanation: Alice can achieve the maximum sum of 9 using a single operation:
- Choose the edge [0,1]. nums[0] becomes: 2 XOR 7 = 5 and nums[1] become: 3 XOR 7 = 4, and the array nums becomes: [2,3] -> [5,4].
The total sum of values is 5 + 4 = 9.
It can be shown that 9 is the maximum achievable sum of values.

Example 3:

Input: nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
Output: 42
Explanation: The maximum achievable sum is 42 which can be achieved by Alice performing no operations.

Constraints:

2 <= n == nums.length <= 2 * 10⁴
1 <= k <= 10⁹
0 <= nums[i] <= 10⁹
edges.length == n - 1
edges[i].length == 2
0 <= edges[i][0], edges[i][1] <= n - 1
The input is generated such that edges represent a valid tree.

Try coding it in LeetCode

Find the Maximum Sum of Node Values #2 Most Asked

Hard

BlackRock

1 view

Topics:

Dynamic ProgrammingGreedy AlgorithmsTreesGraphsBit Manipulation

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 0-indexed 2D integer array edges of length n - 1, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i in the tree. You are also given a positive integer k, and a 0-indexed array of non-negative integers nums of length n, where nums[i] represents the value of the node numbered i.

Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:

Choose any edge [u, v] connecting the nodes u and v, and update their values as follows:
- nums[u] = nums[u] XOR k
- nums[v] = nums[v] XOR k

Return the maximum possible sum of the values Alice can achieve by performing the operation any number of times.

Example 1:

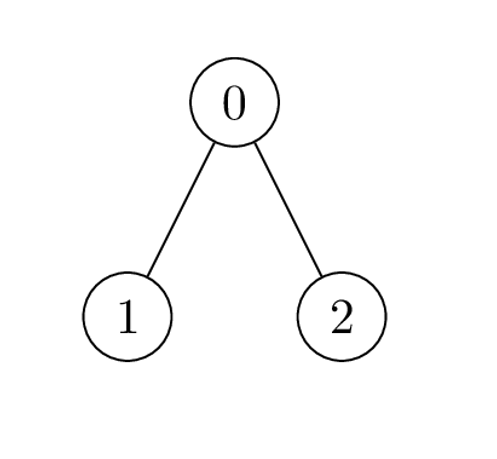
Input: nums = [1,2,1], k = 3, edges = [[0,1],[0,2]]
Output: 6
Explanation: Alice can achieve the maximum sum of 6 using a single operation:
- Choose the edge [0,2]. nums[0] and nums[2] become: 1 XOR 3 = 2, and the array nums becomes: [1,2,1] -> [2,2,2].
The total sum of values is 2 + 2 + 2 = 6.
It can be shown that 6 is the maximum achievable sum of values.

Example 2:

Input: nums = [2,3], k = 7, edges = [[0,1]]
Output: 9
Explanation: Alice can achieve the maximum sum of 9 using a single operation:
- Choose the edge [0,1]. nums[0] becomes: 2 XOR 7 = 5 and nums[1] become: 3 XOR 7 = 4, and the array nums becomes: [2,3] -> [5,4].
The total sum of values is 5 + 4 = 9.
It can be shown that 9 is the maximum achievable sum of values.

Example 3:

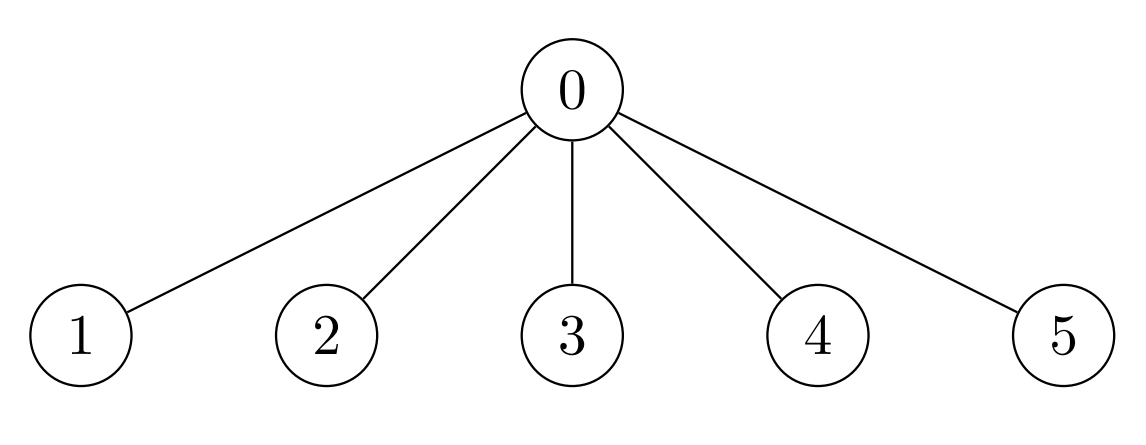
Input: nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]]
Output: 42
Explanation: The maximum achievable sum is 42 which can be achieved by Alice performing no operations.

Constraints:

2 <= n == nums.length <= 2 * 10⁴
1 <= k <= 10⁹
0 <= nums[i] <= 10⁹
edges.length == n - 1
edges[i].length == 2
0 <= edges[i][0], edges[i][1] <= n - 1
The input is generated such that edges represent a valid tree.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the tree contain negative node values?
What is the expected return value if the tree is empty?
Are we guaranteed to have a valid binary tree as input, or should I handle invalid tree structures?
Is it a binary search tree, or a general binary tree?
Are there any constraints on the height or number of nodes in the tree?

Brute Force Solution

Approach

The brute force approach is all about exploring every single path in the tree and calculating the sum of the node values for that path. We'll check every possible path from the root to a leaf. The best path, the one with the largest sum, will be our answer.

Here's how the algorithm would work step-by-step:

Start at the very top of the tree.
Consider one path from the top to the bottom of the tree.
Calculate the sum of all node values along this path.
Remember this sum. It might be the biggest one we've seen so far.
Now, try a different path from the top to the bottom.
Calculate the sum of node values for this new path.
Compare this new sum to the largest sum we've remembered so far. If it's bigger, update the largest sum.
Keep repeating this process for absolutely every single path from the top to the bottom of the tree.
Once you've explored every possible path, the largest sum you've remembered is the answer.

Code Implementation

def find_maximum_path_sum_brute_force(root):
    maximum_sum = float('-inf')

    def calculate_path_sum(node, current_path_sum):
        nonlocal maximum_sum

        if not node:
            return

        current_path_sum += node.value

        # If we've hit a leaf, compare current path sum with the max sum
        if not node.left and not node.right:

            maximum_sum = max(maximum_sum, current_path_sum)
            return

        # Explore the left sub-tree

        calculate_path_sum(node.left, current_path_sum)

        # Explore the right sub-tree

        calculate_path_sum(node.right, current_path_sum)

    # Initiate the recursive traversal from the root node
    calculate_path_sum(root, 0)

    return maximum_sum

Big(O) Analysis

Time Complexity

O(n) – The brute force approach explores every possible path from the root to a leaf in the tree. In a binary tree with 'n' nodes, the number of leaf nodes can be at most n/2. Each path from the root to a leaf has a length proportional to the height of the tree, which in the worst case can be 'n'. The algorithm computes the sum of node values along each path. Therefore, in the worst case, the algorithm explores roughly n/2 paths each of length 'n', however since we only care about the max sum, we only explore each node once to get the path sum. Hence the complexity is O(n).

Space Complexity

O(N) – The provided brute force approach explores all paths from the root to a leaf in the tree. In the worst-case scenario, the tree could be a skewed tree (essentially a linked list), resulting in a recursive call stack depth of N, where N is the number of nodes in the tree. Each recursive call requires storing the current node and the running sum in the call stack. Thus, the auxiliary space used by the recursion stack is proportional to the number of nodes, resulting in O(N) space complexity.

Optimal Solution

Approach

The best way to find the maximum sum is to make strategic decisions at each node. We choose whether to include a node's value based on how it affects the potential maximum sum of its children, considering both scenarios where the node is included and excluded.

Here's how the algorithm would work step-by-step:

Think about each node as having two choices: either be included in the sum or be excluded.
When a node is included, its children cannot be included because that would violate the rule.
When a node is excluded, its children can either be included or excluded; we choose the option that gives the maximum sum for each child.
Start from the bottom of the structure and work your way up. This way, when you reach a node, you've already calculated the maximum sums for its children in both the included and excluded cases.
At each node, calculate two values: the maximum sum if the node is included, and the maximum sum if the node is excluded.
To calculate the maximum sum if the node is included, add the node's value to the maximum sums of its grandchildren (because its children cannot be included).
To calculate the maximum sum if the node is excluded, add the maximum of the included and excluded sums of each of its children.
The final answer is the maximum of the included and excluded sums of the root node (the top-most node).

Code Implementation

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def find_maximum_sum(root):
    def calculate_maximum_sum(node):
        if not node:
            return 0, 0

        left_include, left_exclude = calculate_maximum_sum(node.left)
        right_include, right_exclude = calculate_maximum_sum(node.right)

        # If the current node is included, its children must be excluded.
        include_current_node = node.value + left_exclude + right_exclude

        # If the current node is excluded, choose the max sum of children.
        exclude_current_node = max(left_include, left_exclude) + max(right_include, right_exclude)

        return include_current_node, exclude_current_node

    include_root, exclude_root = calculate_maximum_sum(root)

    # The result is the maximum of including or excluding the root.
    return max(include_root, exclude_root)

Big(O) Analysis

Time Complexity

O(n) – The algorithm visits each node of the structure once, effectively performing a post-order traversal. At each node, a constant amount of work is done to calculate the maximum sums for both the included and excluded cases based on the already computed values of its children. Therefore, the time complexity is directly proportional to the number of nodes, n, in the structure.

Space Complexity

O(N) – The algorithm uses recursion, where each node in the structure potentially results in a recursive call. The maximum depth of the recursion is determined by the height of the structure, which in the worst-case (e.g., a skewed structure) can be proportional to N, where N is the number of nodes. Each level of recursion stores the 'included' and 'excluded' maximum sums for a node. Therefore, the call stack can grow to a size proportional to N, resulting in O(N) auxiliary space. No other significant data structures are explicitly created.

Edge Cases

Case	How to Handle
Null or empty tree	Return 0 if the tree is null or empty, as there are no nodes to sum.
Tree with only one node	Return the value of the single node, as it's the only possible sum.
Tree with only negative node values	Return the largest (least negative) node value, as that will be the maximum sum.
Tree is a very deep, skewed tree (linked list)	Verify that the recursive calls don't exceed the stack limit, or consider converting to iterative approach to manage memory.
Tree with integer overflow potential	Use a larger data type (e.g., long) to store the sum during calculation to avoid integer overflow issues.
Tree with a very large number of nodes approaching memory limits	Consider alternative data structures or algorithms that minimize memory usage if the tree size exceeds available memory.
Node values are all zeros	The maximum sum will be 0 as the sum of any path will result in 0.
Maximum path includes root node, or entirely excludes it	Ensure the algorithm explores all possible paths from the root, considering both inclusion and exclusion of the root node and intermediate nodes.

Null or empty tree

How to Handle:

Return 0 if the tree is null or empty, as there are no nodes to sum.

Tree with only one node

How to Handle:

Return the value of the single node, as it's the only possible sum.

Tree with only negative node values

How to Handle:

Return the largest (least negative) node value, as that will be the maximum sum.

Tree is a very deep, skewed tree (linked list)

How to Handle:

Verify that the recursive calls don't exceed the stack limit, or consider converting to iterative approach to manage memory.

Tree with integer overflow potential

How to Handle:

Use a larger data type (e.g., long) to store the sum during calculation to avoid integer overflow issues.

Tree with a very large number of nodes approaching memory limits

How to Handle:

Consider alternative data structures or algorithms that minimize memory usage if the tree size exceeds available memory.

Node values are all zeros

How to Handle:

The maximum sum will be 0 as the sum of any path will result in 0.

Maximum path includes root node, or entirely excludes it

How to Handle:

Ensure the algorithm explores all possible paths from the root, considering both inclusion and exclusion of the root node and intermediate nodes.