Find the Minimum Area to Cover All Ones II
HardYou are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.
Return the minimum possible sum of the area of these rectangles.
Note that the rectangles are allowed to touch.
Example 1:
Input: grid = [[1,0,1],[1,1,1]]
Output: 5
Explanation:
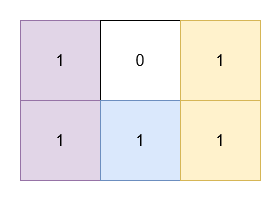
- The 1's at
(0, 0)and(1, 0)are covered by a rectangle of area 2. - The 1's at
(0, 2)and(1, 2)are covered by a rectangle of area 2. - The 1 at
(1, 1)is covered by a rectangle of area 1.
Example 2:
Input: grid = [[1,0,1,0],[0,1,0,1]]
Output: 5
Explanation:
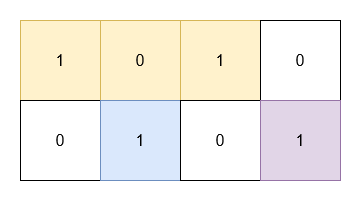
- The 1's at
(0, 0)and(0, 2)are covered by a rectangle of area 3. - The 1 at
(1, 1)is covered by a rectangle of area 1. - The 1 at
(1, 3)is covered by a rectangle of area 1.
Constraints:
1 <= grid.length, grid[i].length <= 30grid[i][j]is either 0 or 1.- The input is generated such that there are at least three 1's in
grid.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix? What are the upper bounds on the number of rows and columns?
- Can the input matrix be empty or contain no '1's? What should I return in those cases?
- Is there a constraint on the number of rectangles I can use to cover the '1's?
- If there are multiple ways to cover the '1's with the minimum area, is any valid solution acceptable, or is there a preferred solution based on some criteria (e.g., minimizing the number of rectangles used)?
- Is the input matrix guaranteed to be rectangular (i.e., all rows have the same number of columns)?
Brute Force Solution
Approach
The brute force approach to finding the smallest rectangle involves trying every possible rectangle size and location on the grid. We check each rectangle to see if it covers all the 'ones'. We then select the smallest such rectangle.
Here's how the algorithm would work step-by-step:
- Start by considering every possible height and width for the rectangle. Start with the smallest possible size and gradually increase it.
- For each height and width combination, slide the rectangle across the grid, placing its top-left corner in every possible position.
- For each rectangle position, check if it covers all the 'ones' in the grid. This means every 'one' must be inside the current rectangle.
- If a rectangle covers all the 'ones', record its area.
- After checking all possible rectangles (size and positions), compare the recorded areas.
- The smallest area among the rectangles that cover all the 'ones' is the answer.
Code Implementation
def find_minimum_area_to_cover_all_ones_brute_force(grid):
rows = len(grid)
cols = len(grid[0])
minimum_area = float('inf')
# Iterate through all possible top-left corners
for top_row in range(rows):
for left_col in range(cols):
# Iterate through all possible bottom-right corners
for bottom_row in range(top_row, rows):
for right_col in range(left_col, cols):
# Check if the current rectangle contains all ones
all_ones_covered = True
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
if not (top_row <= row <= bottom_row and \
left_col <= col <= right_col):
all_ones_covered = False
break
if not all_ones_covered:
break
# Calculate the area and update minimum if applicable
if all_ones_covered:
# Area calculated if all ones are covered
area = (bottom_row - top_row + 1) * (right_col - left_col + 1)
minimum_area = min(minimum_area, area)
# Handle the case where no ones are present in the grid
if minimum_area == float('inf'):
return 0
return minimum_areaBig(O) Analysis
Optimal Solution
Approach
The core idea is to efficiently explore possible rectangle sizes to cover all the 'ones'. We use a smart search method to avoid checking all combinations, focusing on promising rectangle boundaries that are likely to lead to the smallest area.
Here's how the algorithm would work step-by-step:
- First, find the coordinates of all the 'ones' in the grid.
- Sort these 'one' coordinates to help organize our search for rectangles.
- Start with a small possible rectangle that includes at least one 'one'.
- Expand the rectangle's sides, carefully considering which 'ones' are now included inside.
- Check if the expanded rectangle covers all 'ones'. If not, keep expanding until all ones are covered.
- Calculate the area of this rectangle.
- Now, try a different rectangle by shifting its starting position slightly, still making sure to include at least one 'one'.
- Repeat the expanding and area calculation process for this new rectangle.
- Keep track of the smallest area you find among all the rectangles that cover all the 'ones'.
- The smallest area recorded is your final answer.
Code Implementation
def find_minimum_area(grid):
if not grid or not grid[0]:
return 0
rows = len(grid)
cols = len(grid[0])
topmost_row = rows
bottommost_row = -1
leftmost_col = cols
rightmost_col = -1
# Find extreme boundaries of ones
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
topmost_row = min(topmost_row, row)
bottommost_row = max(bottommost_row, row)
leftmost_col = min(leftmost_col, col)
rightmost_col = max(rightmost_col, col)
# No ones found
if topmost_row > bottommost_row:
return 0
minimum_area = (bottommost_row - topmost_row + 1) * \
(rightmost_col - leftmost_col + 1)
# Iterate through possible top boundaries.
for top in range(topmost_row, bottommost_row + 1):
for left in range(leftmost_col, rightmost_col + 1):
for bottom in range(bottommost_row, top - 1, -1):
for right in range(rightmost_col, left - 1, -1):
is_valid = True
# Verify that the rectangle covers all ones
for row in range(rows):
for col in range(cols):
if grid[row][col] == 1:
if not (top <= row <= bottom and \
left <= col <= right):
is_valid = False
break
if not is_valid:
break
# If the rectangle is valid, update the min area
if is_valid:
area = (bottom - top + 1) * (right - left + 1)
minimum_area = min(minimum_area, area)
return minimum_areaBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 since there are no '1's to cover. |
| Grid with no '1's | Return 0 as no rectangles are needed. |
| Grid with all '1's | Calculate the area of the entire grid as a single rectangle. |
| Grid with a single '1' | Return 1, representing a 1x1 rectangle. |
| Very large grid dimensions (potential integer overflow for area) | Use long data type to store intermediate and final area results to avoid overflow. |
| Grid where all '1's are in a single row or column | The solution should optimally create a single rectangle covering the entire row/column of '1's. |
| Grid with '1's clustered in multiple disjoint regions | The solution should correctly compute the minimum area to cover all '1's, which will be the sum of areas covering each region. |
| Grid with extreme aspect ratio (very wide and short or very tall and narrow) | The algorithm's performance should not be significantly affected by the grid's aspect ratio. |