Find the Number of Ways to Place People II
HardYou are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].
We define the right direction as positive x-axis (increasing x-coordinate) and the left direction as negative x-axis (decreasing x-coordinate). Similarly, we define the up direction as positive y-axis (increasing y-coordinate) and the down direction as negative y-axis (decreasing y-coordinate)
You have to place n people, including Alice and Bob, at these points such that there is exactly one person at every point. Alice wants to be alone with Bob, so Alice will build a rectangular fence with Alice's position as the upper left corner and Bob's position as the lower right corner of the fence (Note that the fence might not enclose any area, i.e. it can be a line). If any person other than Alice and Bob is either inside the fence or on the fence, Alice will be sad.
Return the number of pairs of points where you can place Alice and Bob, such that Alice does not become sad on building the fence.
Note that Alice can only build a fence with Alice's position as the upper left corner, and Bob's position as the lower right corner. For example, Alice cannot build either of the fences in the picture below with four corners (1, 1), (1, 3), (3, 1), and (3, 3), because:
- With Alice at
(3, 3)and Bob at(1, 1), Alice's position is not the upper left corner and Bob's position is not the lower right corner of the fence. - With Alice at
(1, 3)and Bob at(1, 1), Bob's position is not the lower right corner of the fence.

Example 1:
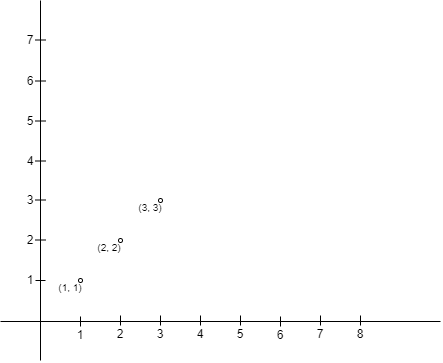
Input: points = [[1,1],[2,2],[3,3]] Output: 0 Explanation: There is no way to place Alice and Bob such that Alice can build a fence with Alice's position as the upper left corner and Bob's position as the lower right corner. Hence we return 0.
Example 2:

Input: points = [[6,2],[4,4],[2,6]] Output: 2 Explanation: There are two ways to place Alice and Bob such that Alice will not be sad: - Place Alice at (4, 4) and Bob at (6, 2). - Place Alice at (2, 6) and Bob at (4, 4). You cannot place Alice at (2, 6) and Bob at (6, 2) because the person at (4, 4) will be inside the fence.
Example 3:

Input: points = [[3,1],[1,3],[1,1]] Output: 2 Explanation: There are two ways to place Alice and Bob such that Alice will not be sad: - Place Alice at (1, 1) and Bob at (3, 1). - Place Alice at (1, 3) and Bob at (1, 1). You cannot place Alice at (1, 3) and Bob at (3, 1) because the person at (1, 1) will be on the fence. Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid.
Constraints:
2 <= n <= 1000points[i].length == 2-109 <= points[i][0], points[i][1] <= 109- All
points[i]are distinct.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the data types and ranges for `n`, `m`, and the coordinates in the `points` array? Are they all non-negative integers?
- Can there be any overlapping areas where people are sitting (i.e., where the area covered by one person's vision overlaps with another's)?
- If no placement is possible, what should the function return? Should it return 0, or is there a specific error code or exception?
- Can the input array `points` be empty or null? If so, how should I handle that case?
- Are there any constraints on the placement of people, such as they must be fully within the grid (i.e., their vision radius doesn't extend beyond the grid boundaries)? If so, what happens if it does?
Brute Force Solution
Approach
The brute force approach involves checking every single possible arrangement of people on the grid to see if it's a valid placement. We generate all combinations and verify each one individually. This is simple to understand but very inefficient.
Here's how the algorithm would work step-by-step:
- First, imagine trying to place the first person in every possible location on the grid.
- For each of these locations, try placing the second person in every possible location.
- Continue this process for each person, trying all possible locations for them, one at a time, considering all previous placements.
- For each complete arrangement of people, check if it's valid. An arrangement is valid if no two people are within the specified attack range of each other.
- To check the attack range, for each pair of people in the arrangement, calculate the distance between them and see if it's less than or equal to the attack range.
- If the arrangement is valid (no people are within the attack range of each other), count it as a valid placement.
- After trying all possible arrangements, return the total count of valid placements you found.
Code Implementation
def find_the_number_of_ways_to_place_people_brute_force(
grid_rows,
grid_cols,
number_of_people,
attack_distance):
valid_placements_count = 0
def is_valid_placement(people_locations):
# Check if any two people are within the attack distance.
for i in range(len(people_locations)):
for j in range(i + 1, len(people_locations)):
row_difference = abs(people_locations[i][0] - people_locations[j][0])
col_difference = abs(people_locations[i][1] - people_locations[j][1])
distance = (row_difference**2 + col_difference**2)**0.5
if distance <= attack_distance:
return False
return True
def generate_placements(current_people_locations):
nonlocal valid_placements_count
if len(current_people_locations) == number_of_people:
# Found complete placement, check for validity.
if is_valid_placement(current_people_locations):
valid_placements_count += 1
return
# Try all possible locations for the next person.
for row in range(grid_rows):
for col in range(grid_cols):
new_person_location = (row, col)
generate_placements(current_people_locations + [new_person_location])
generate_placements([])
return valid_placements_countBig(O) Analysis
Optimal Solution
Approach
The key idea is to avoid double-counting arrangements by processing people in a specific order. We'll use sorted coordinates to avoid considering duplicate placements and leverage the information from previously placed people to make efficient calculations. We'll work with the sorted information to calculate possible valid placements in a non-redundant way.
Here's how the algorithm would work step-by-step:
- First, sort the list of people by their x-coordinate, and if x-coordinates are equal, sort by their y-coordinate.
- Go through the sorted list of people one at a time.
- For each person, count how many earlier placed people are within their visibility range (i.e., to their left and below).
- Subtract this count from the total number of available spots within the grid that are also to their left and below the person.
- This gives you the number of valid new spots where this person can be placed without overlapping the visibility range of any previous person.
- Multiply the number of valid new spots by the number of ways you could have placed the earlier people.
- Keep a running total of the valid ways to place each person.
- The final total will be the total number of valid ways to place all people.
Code Implementation
def find_number_of_ways_to_place_people(grid_row_size, grid_column_size, people):
people.sort(key=lambda person: (person[0], person[1]))
total_ways = 0
# Iterate over all possible placements of the first person
for first_person_row in range(people[0][0] + 1):
for first_person_col in range(people[0][1] + 1):
current_ways = 1
# This variable keeps track of valid placements
valid_placement = True
#Iterate over the other people
for i in range(1, len(people)):
person_row = people[i][0]
person_col = people[i][1]
invalid_spots = 0
# Count invalid spots due to previous people
for j in range(i):
previous_person_row = people[j][0]
previous_person_col = people[j][1]
if first_person_row <= previous_person_row and first_person_col <= previous_person_col:
invalid_spots += 1
# Count number of valid spots for the person.
available_spots_for_person = (person_row + 1) * (person_col + 1)
valid_spots = available_spots_for_person - invalid_spots
#If we can't place this person, this is an invalid starting position
if valid_spots <= 0:
valid_placement = False
break
current_ways *= valid_spots
# Add total ways if valid placement is True
if valid_placement:
total_ways += current_ways
return total_waysBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| people is null or empty | Return 0 immediately as no placements are possible. |
| width or height is zero or negative | If width or height is zero, return 0; negative values are invalid dimensions, so return 0 as well. |
| people contains duplicate coordinates | Consider each location uniquely regardless of duplicates, effectively treating each coordinate pair as a distinct placement possibility |
| People are located on the boundary (0,0), (width,height) | Handle boundary locations normally within the coordinate constraints. |
| Extremely large width and height values that could lead to integer overflow | Use long data types for width and height calculations to avoid integer overflow. |
| radius is larger than width or height | Handle it based on problem constaints; the effective area still depends on actual points and radius calculation, use long to prevent overflows here as well |
| All people are clustered in a small region | The solution should still correctly count valid placements within that region. |
| No possible placements are available | Return 0 when no valid location can satisfy the radius constraint for any person. |