First Completely Painted Row or Column #16 Most Asked
MediumYou are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].
Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].
Return the smallest index i at which either a row or a column will be completely painted in mat.
Example 1:
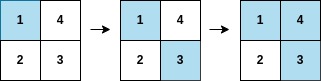
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]] Output: 2 Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].
Example 2:
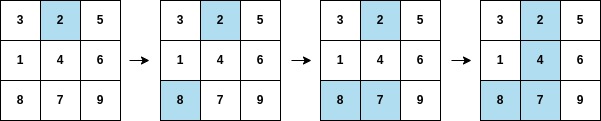
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]] Output: 3 Explanation: The second column becomes fully painted at arr[3].
Constraints:
m == mat.lengthn = mat[i].lengtharr.length == m * n1 <= m, n <= 1051 <= m * n <= 1051 <= arr[i], mat[r][c] <= m * n- All the integers of
arrare unique. - All the integers of
matare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix, and what is the range of values within the matrix?
- What should I return if no row or column is fully painted after all cells are marked?
- How is the 'painting' represented? Is it a separate data structure tracking which cells are painted, or is it implicit?
- If multiple rows or columns are painted on the same move, should I return the index of the first painted row/column, or is any valid index acceptable?
- Can I assume that the input list of cells to paint contains valid coordinates within the matrix's dimensions?
Brute Force Solution
Approach
The goal is to find the first row or column that gets completely filled in as we process a sequence of painting operations. The brute force way is simply to simulate all the painting operations step-by-step, checking after each one whether a row or column has been fully painted.
Here's how the algorithm would work step-by-step:
- Start with a blank grid representing the rows and columns, where nothing is painted yet.
- Take the first painting instruction and mark that cell in the grid as painted.
- After painting that cell, check if every cell in its row is painted. If so, you've found the first fully painted row, and you're done.
- Also, check if every cell in its column is painted. If so, you've found the first fully painted column, and you're done.
- If neither the row nor the column is fully painted, move to the next painting instruction.
- Repeat steps 2-4 for each painting instruction until you find a fully painted row or column, or until you've processed all the instructions.
Code Implementation
def first_completely_painted_row_or_column(rows, cols, paint_instructions):
grid = [[False] * cols for _ in range(rows)]
for step, (row_index, col_index) in enumerate(paint_instructions):
# Mark the current cell as painted.
grid[row_index][col_index] = True
# Check if the current row is fully painted.
row_painted = all(grid[row_index])
if row_painted:
return step + 1
# Check if the current column is fully painted.
column_painted = all(grid[i][col_index] for i in range(rows))
if column_painted:
return step + 1
return -1Big(O) Analysis
Optimal Solution
Approach
The key is to efficiently track which rows and columns are fully painted. We can avoid repeatedly checking the entire board after each paint operation. Instead, we maintain separate counters to determine when a row or column has been completely painted.
Here's how the algorithm would work step-by-step:
- Keep track of how many cells are painted in each row.
- Keep track of how many cells are painted in each column.
- When you paint a cell, increase the row counter for that row.
- When you paint a cell, increase the column counter for that column.
- After each paint operation, check if any row's counter equals the number of columns.
- If a row is fully painted, you've found your answer. Return the step when this happened.
- After each paint operation, check if any column's counter equals the number of rows.
- If a column is fully painted, you've found your answer. Return the step when this happened.
- If no row or column is fully painted after all the operations, return -1 to indicate that.
Code Implementation
def first_completely_painted_row_or_column(board_rows, board_columns, paint_steps):
number_of_rows = len(board_rows)
number_of_columns = len(board_columns)
row_counts = [0] * number_of_rows
column_counts = [0] * number_of_columns
for step, (row_index, column_index) in enumerate(paint_steps):
# Increment row and column counts after each paint step.
row_counts[row_index] += 1
column_counts[column_index] += 1
# Check if any row is fully painted.
for i in range(number_of_rows):
if row_counts[i] == number_of_columns:
return step + 1
#Check if any column is fully painted
for j in range(number_of_columns):
if column_counts[j] == number_of_rows:
return step + 1
# Return -1 if no row or column is fully painted.
return -1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty input matrix (either rows or cols is 0) | Return -1 immediately as no row or column can be fully painted. |
| Matrix with only one row or one column | Iterate through the input array 'arr' to check when this single row or column gets fully painted and return the index. |
| All elements in 'arr' paint the same cell (highly skewed input) | The solution should still iterate through 'arr', updating the painted rows and columns, eventually finding the completion time. |
| No row or column is ever fully painted | Return -1 after iterating through the entire 'arr' because no row or column was completely painted. |
| Duplicate numbers in the input matrix | Store only the latest index of appearance for each number in the matrix, which correctly reflects the last time a cell was painted. |
| Large matrix dimensions potentially leading to memory issues | Use efficient data structures like sets or bitmaps if memory becomes a bottleneck for tracking painted rows and columns. |
| Input 'arr' contains values not present in the matrix | Ignore these values, as they represent painting actions outside the boundaries of the matrix and don't contribute to painting rows/columns. |
| Integer overflow when calculating row/column completion count if the matrix is extremely large | Use a larger integer type (e.g., long) or consider using a boolean array to track completion instead of counting to avoid overflow. |