Flip Equivalent Binary Trees #18 Most Asked
MediumFor a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.
Example 1:
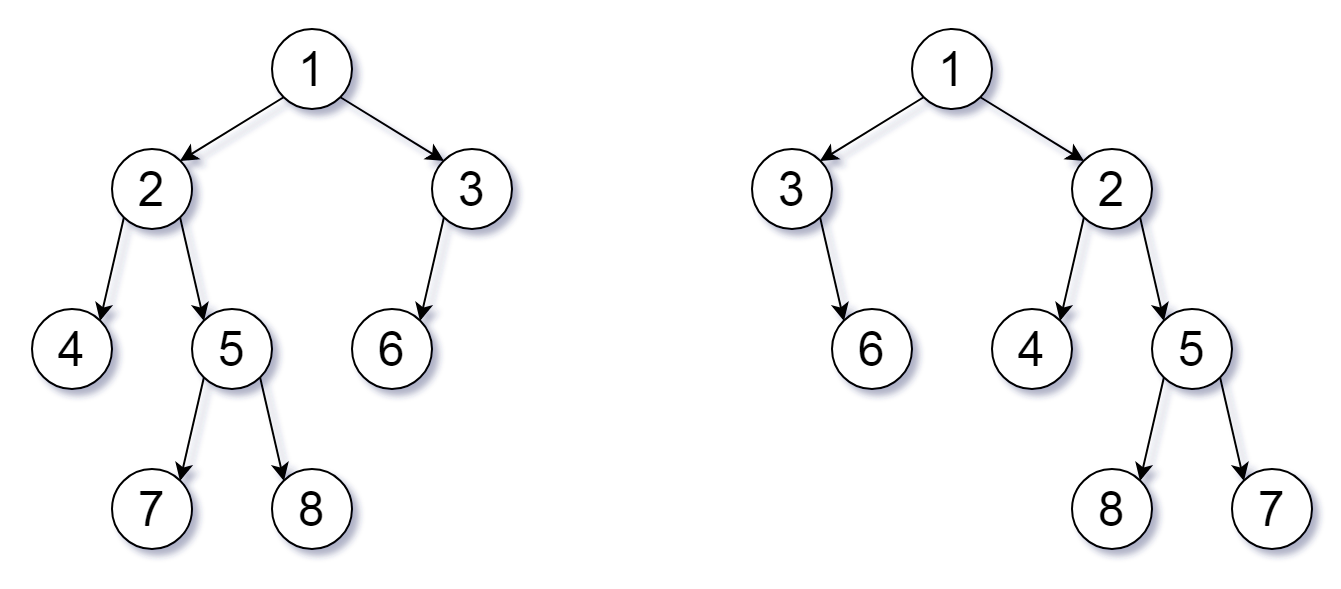
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7] Output: true Explanation: We flipped at nodes with values 1, 3, and 5.
Example 2:
Input: root1 = [], root2 = [] Output: true
Example 3:
Input: root1 = [], root2 = [1] Output: false
Constraints:
- The number of nodes in each tree is in the range
[0, 100]. - Each tree will have unique node values in the range
[0, 99].
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the binary trees can hold?
- Can the trees be empty (null)? If so, what should I return?
- By 'flip equivalent', do you mean that only the structure must be the same, or do the node values also have to be equal for the trees to be considered equivalent?
- If the trees are structurally the same but have different values at corresponding nodes, should I return false?
- Are we only concerned with binary trees, meaning each node has at most two children?
Brute Force Solution
Approach
The brute-force approach to check if two binary trees are flip equivalent involves exploring every single possible combination of flips within one of the trees. We compare the structures of the trees after each possible flip to see if they match.
Here's how the algorithm would work step-by-step:
- First, check if both trees are empty. If they are, they're flip equivalent!
- If only one tree is empty, they are not flip equivalent.
- If the root values of the two trees are different, then they are not flip equivalent.
- Now, consider the first tree. Try flipping the left and right children.
- Then, compare the structure of the modified first tree with the second tree to see if they are identical (recursively check the left and right subtrees).
- Next, revert the flip we did earlier, so the first tree is back to its original state.
- Now, compare the original structure of the first tree with the second tree (recursively check the left and right subtrees).
- If either of these comparisons (with the flip or without the flip) shows the trees are identical, they are flip equivalent. Otherwise, they are not.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def flip_equivalent_binary_trees(root1, root2):
if not root1 and not root2:
return True
if not root1 or not root2:
return False
if root1.value != root2.value:
return False
# Attempt flipping the nodes to find equivalence
root1.left, root1.right = root1.right, root1.left
# Check if flip makes the trees equivalent
if flip_equivalent_binary_trees(root1.left, root2.left) and \
flip_equivalent_binary_trees(root1.right, root2.right):
return True
# Revert the flip to check original structure
root1.left, root1.right = root1.right, root1.left
#Check if original structure is equivalent
if flip_equivalent_binary_trees(root1.left, root2.left) and \
flip_equivalent_binary_trees(root1.right, root2.right):
return True
# If no configuration matches, they are not flip equivalent
return FalseBig(O) Analysis
Optimal Solution
Approach
We need to determine if two binary trees are flip-equivalent, meaning one can be transformed into the other by flipping some nodes. The key is to recursively check if the current nodes are swappable while ensuring the subtrees also satisfy the flip-equivalence condition.
Here's how the algorithm would work step-by-step:
- First, check if both trees are empty. If so, they are flip-equivalent.
- If only one of the trees is empty, they are not flip-equivalent.
- Next, see if the values at the current nodes of both trees are the same. If not, they are not flip-equivalent.
- Now, consider the left and right subtrees of both trees. There are two possibilities for flip-equivalence: either the left subtree of tree A is equivalent to the left subtree of tree B AND the right subtree of tree A is equivalent to the right subtree of tree B, OR the left subtree of tree A is equivalent to the right subtree of tree B AND the right subtree of tree A is equivalent to the left subtree of tree B.
- Recursively apply these checks to the subtrees. Return true if any of these conditions are met, indicating that the trees are flip-equivalent.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def flip_equiv(root1, root2):
if not root1 and not root2:
return True
if not root1 or not root2:
return False
if root1.value != root2.value:
return False
# Check without flipping
without_flip = flip_equiv(root1.left, root2.left) and \
flip_equiv(root1.right, root2.right)
# Check with flipping
# Check if left of tree1 equals the right of tree2.
with_flip = flip_equiv(root1.left, root2.right) and \
flip_equiv(root1.right, root2.left)
# Return if either flip or no flip are True
# Return True if one case matches, else False.
return without_flip or with_flipBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both input trees are null | Return True as two null trees are considered flip equivalent. |
| One tree is null, and the other is not | Return False as one tree must be flipped to match the null tree, which is impossible. |
| Trees with a single node | If both single nodes have same value, return True, otherwise return False. |
| Trees with identical structure and values | Return True without flipping. |
| Trees with different root values | Return False immediately since flipping won't change root values. |
| Skewed trees (highly unbalanced) | The recursive calls will handle skewed trees correctly up to the recursion depth limit. |
| Trees with duplicate values at different levels | The algorithm correctly explores both flipped and non-flipped options to find a match. |
| Very large trees exceeding recursion depth | Consider converting the recursive solution to an iterative solution using a stack to avoid exceeding recursion limits. |