Flood Fill
EasyYou are given an image represented by an m x n grid of integers image, where image[i][j] represents the pixel value of the image. You are also given three integers sr, sc, and color. Your task is to perform a flood fill on the image starting from the pixel image[sr][sc].
To perform a flood fill:
- Begin with the starting pixel and change its color to
color. - Perform the same process for each pixel that is directly adjacent (pixels that share a side with the original pixel, either horizontally or vertically) and shares the same color as the starting pixel.
- Keep repeating this process by checking neighboring pixels of the updated pixels and modifying their color if it matches the original color of the starting pixel.
- The process stops when there are no more adjacent pixels of the original color to update.
Return the modified image after performing the flood fill.
Example 1:
Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, color = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation:
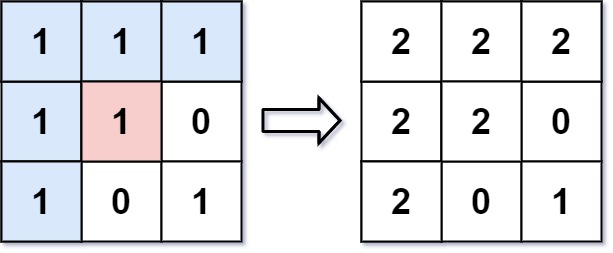
From the center of the image with position (sr, sc) = (1, 1) (i.e., the red pixel), all pixels connected by a path of the same color as the starting pixel (i.e., the blue pixels) are colored with the new color.
Note the bottom corner is not colored 2, because it is not horizontally or vertically connected to the starting pixel.
Example 2:
Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, color = 0
Output: [[0,0,0],[0,0,0]]
Explanation:
The starting pixel is already colored with 0, which is the same as the target color. Therefore, no changes are made to the image.
Constraints:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], color < 2160 <= sr < m0 <= sc < n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions (rows and columns) constraints for the input `image`? Can I assume the image is rectangular (i.e., all rows have the same number of columns)?
- What is the range of possible values for the colors in the image, the `color`, and the original color at `image[sr][sc]`? Can the new `color` be the same as the original color at `image[sr][sc]`?
- Are the starting row `sr` and starting column `sc` guaranteed to be within the bounds of the `image` array? If not, what should I return or how should I handle out-of-bounds indices?
- Is the input image guaranteed to be valid, or could it be null or empty? What should I return in those cases?
- Should the algorithm modify the original image in place, or return a new image with the flood fill applied?
Brute Force Solution
Approach
The flood fill problem asks us to change a connected area of one color to another color. The brute force strategy will look at each spot individually, one by one, and update the color if necessary. We will repeat this until no more changes are needed.
Here's how the algorithm would work step-by-step:
- Start at the given starting spot.
- Check if the starting spot's current color matches the original color we're trying to replace.
- If it does, change the color of this spot to the new color.
- Now, look at the spots directly above, below, to the left, and to the right of the starting spot.
- For each of these neighbor spots, check if its color matches the original color.
- If a neighbor's color matches the original color, change its color to the new color.
- Repeat steps 4-6 for each of the neighbor spots that you just changed. Keep doing this until you've checked every connected spot with the original color.
- Continue until there are no more neighbor spots with the original color left to change.
Code Implementation
def flood_fill_brute_force(image, start_row, start_column, new_color):
original_color = image[start_row][start_column]
# No work to do if the starting color is already the new color
if original_color == new_color:
return image
rows = len(image)
columns = len(image[0])
cells_to_process = [(start_row, start_column)]
while cells_to_process:
row, column = cells_to_process.pop(0)
# Only process cells within the image bounds
if 0 <= row < rows and 0 <= column < columns and image[row][column] == original_color:
# Change the color of the current cell
image[row][column] = new_color
# Add neighboring cells to be processed
if row > 0:
cells_to_process.append((row - 1, column))
if row < rows - 1:
cells_to_process.append((row + 1, column))
if column > 0:
cells_to_process.append((row, column - 1))
if column < columns - 1:
cells_to_process.append((row, column + 1))
return imageBig(O) Analysis
Optimal Solution
Approach
The flood fill problem involves changing a region of the same color to a new color, starting from a given point. The best way to do this is to explore outward from the starting point, changing colors as you go until you hit the boundaries of the original colored region.
Here's how the algorithm would work step-by-step:
- Start at the given starting point.
- Check if the starting point's color is the same as the new color. If they are the same, there's nothing to do, so stop.
- Change the color of the starting point to the new color.
- Look at the neighbors (up, down, left, right) of the current point.
- For each neighbor, check if its color is the same as the original color of the starting point.
- If a neighbor has the same color as the original, change its color to the new color, and then repeat this process for *that* neighbor. It is crucial to continue the process with this neighbor right away!
- Continue this process of changing colors and looking at neighbors until you've explored every point connected to the starting point that had the original color.
Code Implementation
def flood_fill(image, start_row, start_column, new_color):
number_of_rows = len(image)
number_of_columns = len(image[0])
original_color = image[start_row][start_column]
# If new color is the same as original, no need to flood fill
if original_color == new_color:
return image
def explore_neighbors(row, column):
# Check boundaries and original color
if row < 0 or row >= number_of_rows or column < 0 or column >= number_of_columns or image[row][column] != original_color:
return
image[row][column] = new_color
# Recursively fill neighbors
explore_neighbors(row + 1, column)
explore_neighbors(row - 1, column)
explore_neighbors(row, column + 1)
explore_neighbors(row, column - 1)
# Initiate the flood fill
explore_neighbors(start_row, start_column)
return imageBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty image | Return the image immediately if it's null or empty as there's nothing to process. |
| sr or sc are out of bounds | Return the original image immediately if sr or sc are out of bounds of the image dimensions. |
| New color is the same as the starting pixel's color | Return the original image immediately since no changes are needed if the new color matches the initial color. |
| Image is a single pixel | If the image is a single pixel and the new color is different, change the pixel's color and return. |
| Image is a large matrix (potential stack overflow with recursion) | Use iterative approach (e.g., using a queue) instead of recursion to avoid stack overflow issues for large images. |
| Image contains only one color | The algorithm should correctly change all pixels to the new color if the starting color matches the single color in the image. |
| Integer overflow possible if image dimensions are very large leading to very large number of recursive calls or large queue size | While unlikely to cause integer overflow in most languages for reasonable image sizes, memory usage is key and iterative solution can alleviate this problem as well. |
| Maximum call stack size exceeded due to recursion depth | Convert the recursive solution to an iterative one using a queue to avoid stack overflow issues. |