Get Biggest Three Rhombus Sums in a Grid

Medium

Asked by:

1 view

Topics:

Arrays

You are given an m x n integer matrix grid.

A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:

Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.

Return the biggest three distinct rhombus sums in the grid in descending order. If there are less than three distinct values, return all of them.

Example 1:

Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
Output: [228,216,211]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211

Example 2:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: [20,9,8]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)

Example 3:

Input: grid = [[7,7,7]]
Output: [7]
Explanation: All three possible rhombus sums are the same, so return [7].

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10⁵

Get Biggest Three Rhombus Sums in a Grid

Medium

Asked by:

1 view

Topics:

Arrays

You are given an m x n integer matrix grid.

A rhombus sum is the sum of the elements that form the border of a regular rhombus shape in grid. The rhombus must have the shape of a square rotated 45 degrees with each of the corners centered in a grid cell. Below is an image of four valid rhombus shapes with the corresponding colored cells that should be included in each rhombus sum:

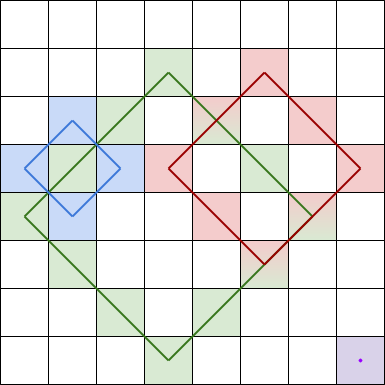
Note that the rhombus can have an area of 0, which is depicted by the purple rhombus in the bottom right corner.

Return the biggest three distinct rhombus sums in the grid in descending order. If there are less than three distinct values, return all of them.

Example 1:

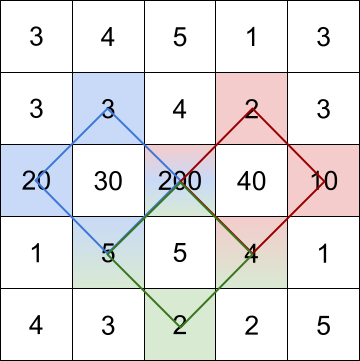
Input: grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
Output: [228,216,211]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 20 + 3 + 200 + 5 = 228
- Red: 200 + 2 + 10 + 4 = 216
- Green: 5 + 200 + 4 + 2 = 211

Example 2:

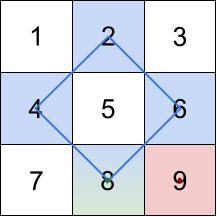
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: [20,9,8]
Explanation: The rhombus shapes for the three biggest distinct rhombus sums are depicted above.
- Blue: 4 + 2 + 6 + 8 = 20
- Red: 9 (area 0 rhombus in the bottom right corner)
- Green: 8 (area 0 rhombus in the bottom middle)

Example 3:

Input: grid = [[7,7,7]]
Output: [7]
Explanation: All three possible rhombus sums are the same, so return [7].

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10⁵

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the dimensions of the grid (rows and columns)? What is the maximum possible size?
What is the range of integer values within the grid? Can I expect negative values, zero, or only positive values?
How is a rhombus defined? Specifically, must the rhombus be centered at a cell within the grid and have sides parallel to the grid's diagonals?
If fewer than three distinct rhombus sums exist, should I return all existing distinct sums, or pad the result with a default value like negative infinity or null?
In the case of ties (e.g., multiple rhombuses having the same sum), how should I handle the selection of the top three sums? Do I need to return all the rhombus sums in descending order even when the sizes are more than three?

Brute Force Solution

Approach

The brute force approach to finding the biggest rhombus sums in a grid is all about trying every possible rhombus we can make. We calculate the sum for each one and keep track of the biggest three sums we've seen.

Here's how the algorithm would work step-by-step:

First, consider every single cell in the grid as the center of a potential rhombus.
For each center, try making rhombuses of all possible sizes, starting from a size of one (just the center cell itself).
To make a bigger rhombus, extend its sides diagonally outward from the center cell by one cell at a time.
At each size, calculate the sum of all the numbers that make up that rhombus.
Keep track of the sums of all the rhombuses you calculate.
After checking every possible rhombus size from every possible center, you will have a list of all the rhombus sums.
From this list, find the three biggest unique rhombus sums. If there are fewer than three unique sums, return the unique sums that you do have.

Code Implementation

def get_biggest_three_rhombus_sums(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])
    rhombus_sums = set()

    for row_index in range(number_of_rows):
        for column_index in range(number_of_columns):
            # Iterate through all possible centers.
            for rhombus_size in range(1, min(number_of_rows, number_of_columns) + 1):
                if row_index - rhombus_size + 1 < 0 or \
                   row_index + rhombus_size - 1 >= number_of_rows or \
                   column_index - rhombus_size + 1 < 0 or \
                   column_index + rhombus_size - 1 >= number_of_columns:
                    continue

                rhombus_sum = 0
                # Calculate the rhombus sum.
                for i in range(rhombus_size):
                    rhombus_sum += grid[row_index - rhombus_size + 1 + i][column_index + i]
                    if i > 0:
                        rhombus_sum += grid[row_index - rhombus_size + 1 + i][column_index - i]
                    rhombus_sum += grid[row_index + rhombus_size - 1 - i][column_index + i]
                    if i > 0:
                        rhombus_sum += grid[row_index + rhombus_size - 1 - i][column_index - i]

                rhombus_sums.add(rhombus_sum)

    # Get the top 3 unique rhombus sums.
    rhombus_sums_list = sorted(list(rhombus_sums), reverse=True)

    # Returning biggest sums.
    return rhombus_sums_list[:3]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n * min(m, n)) – We iterate through each cell (m * n) in the grid as a potential center. For each center, the rhombus size can increase until it hits the boundary of the grid. The maximum size of the rhombus's side is bounded by min(m, n). For each size, calculating the rhombus sum takes constant time (O(1)). Thus, the overall time complexity becomes O(m * n * min(m, n)), where m and n are the dimensions of the grid.

Space Complexity

O(N^2) – The algorithm keeps track of the sums of all rhombuses calculated. In the worst-case scenario, every cell could potentially be the center of a rhombus, and for each center, multiple rhombus sizes can be formed. This implies potentially storing a number of rhombus sums proportional to the number of cells in the grid, which is related to the area of the grid. Therefore, we are keeping track of unique sums in a list. In the worst case, all sums are distinct potentially leading to a list with a number of elements that can be proportional to N^2, where N is the maximum dimension of the grid. The extraction of three largest unique rhombus sums doesn't add any meaningful asymptotic space overhead.

Optimal Solution

Approach

The key to efficiently finding the largest rhombus sums is to pre-compute diagonal sums. This avoids redundant calculations and makes finding rhombus sums much faster. We then collect the top three unique rhombus sums.

Here's how the algorithm would work step-by-step:

Calculate the sums of all possible diagonals going in both directions (top-left to bottom-right, and top-right to bottom-left) in the grid and save them.
For every cell in the grid, consider it as the center of a potential rhombus of increasing size.
Use the pre-computed diagonal sums to calculate the sum of each rhombus centered at the current cell. To do this, you will add up sections of the pre-calculated diagonals.
Store each rhombus sum in a collection, but only if it's not a duplicate of a previously calculated sum.
Once all possible rhombus sums are calculated and stored, sort these unique sums in descending order.
Return the top three largest unique rhombus sums. If there are fewer than three unique sums, return all of them.

Code Implementation

def get_biggest_three_rhombus_sums(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    # Store diagonal sums to avoid recomputation
    top_left_to_bottom_right_diagonals = {}
    top_right_to_bottom_left_diagonals = {}

    for row in range(number_of_rows):
        for col in range(number_of_columns):
            for diagonal_length in range(min(number_of_rows, number_of_columns)):  
                if row - diagonal_length >= 0 and col - diagonal_length >= 0:
                    if (row, col, diagonal_length) not in top_left_to_bottom_right_diagonals:
                        top_left_to_bottom_right_diagonals[(row, col, diagonal_length)] = 0

                    top_left_to_bottom_right_diagonals[(row, col, diagonal_length)] += \
                        grid[row - diagonal_length][col - diagonal_length]

                if row - diagonal_length >= 0 and col + diagonal_length < number_of_columns:
                    if (row, col, diagonal_length) not in top_right_to_bottom_left_diagonals:
                        top_right_to_bottom_left_diagonals[(row, col, diagonal_length)] = 0

                    top_right_to_bottom_left_diagonals[(row, col, diagonal_length)] += \
                        grid[row - diagonal_length][col + diagonal_length]

    rhombus_sums = set()

    for row in range(number_of_rows):
        for col in range(number_of_columns):
            rhombus_sums.add(grid[row][col])

            for rhombus_size in range(1, min(number_of_rows, number_of_columns)):
                if row - rhombus_size >= 0 and row + rhombus_size < number_of_rows and \
                   col - rhombus_size >= 0 and col + rhombus_size < number_of_columns:

                    # Use precomputed diagonal sums to calculate rhombus sum efficiently
                    rhombus_sum = grid[row][col]

                    rhombus_sum += top_left_to_bottom_right_diagonals[(row + rhombus_size, col + rhombus_size, rhombus_size - 1)]
                    rhombus_sum += top_right_to_bottom_left_diagonals[(row + rhombus_size, col - rhombus_size, rhombus_size - 1)]
                    rhombus_sum += top_left_to_bottom_right_diagonals[(row - rhombus_size, col - rhombus_size, rhombus_size - 1)]
                    rhombus_sum += top_right_to_bottom_left_diagonals[(row - rhombus_size, col + rhombus_size, rhombus_size - 1)]

                    rhombus_sums.add(rhombus_sum)

    # Sort the unique sums in descending order
    sorted_rhombus_sums = sorted(list(rhombus_sums), reverse=True)

    # Return the top three largest sums or all if fewer than three
    return sorted_rhombus_sums[:3]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n * min(m, n)) – Pre-computing diagonal sums takes O(m * n) where m is the number of rows and n is the number of columns. The dominant part is iterating through each cell in the grid (O(m * n)) and considering it as the center of a rhombus. For each cell, the rhombus size can grow up to min(m, n). For each rhombus size, we perform constant time operations using precomputed diagonal sums. Therefore, the nested iterations result in a time complexity of O(m * n * min(m, n)). Sorting the unique rhombus sums can be done in O(k log k) where k is the number of unique sums, but it's still bounded by m*n*min(m,n) so sorting doesn't change the overall complexity.

Space Complexity

O(N^2) – The algorithm pre-computes diagonal sums and stores them. Since there are two sets of diagonals (top-left to bottom-right and top-right to bottom-left) and the number of diagonals in a grid of size N x N is proportional to N, storing these diagonal sums will require O(N^2) space. Additionally, the algorithm stores unique rhombus sums. In the worst case, the number of unique rhombus sums can also be proportional to N^2. Therefore, the auxiliary space complexity is O(N^2). The storage of the top three results is constant and does not affect the overall space complexity.

Edge Cases

Case	How to Handle
Null or empty grid	Return an empty list immediately since no rhombus sums can be calculated.
Grid with only one row or one column	The maximum possible rhombus side length is zero, so consider each cell a rhombus, and return the top three unique cell values.
Grid with all identical values	The top three rhombus sums will consist of the same value repeated, possibly less than three times if there aren't enough unique rhombus sizes.
Grid with negative numbers	The algorithm should correctly handle negative numbers in the grid when calculating rhombus sums.
Grid with large positive numbers that could cause integer overflow	Use a data type with a larger range (e.g., long) for storing intermediate sums to prevent overflow.
Maximum grid size where the calculation becomes computationally expensive	Optimize the rhombus sum calculation to avoid redundant computations, possibly pre-calculating partial sums or using memoization if the same rhombus shapes are being calculated repeatedly.
Duplicate rhombus sums should only be counted once in the top three	Use a set to store the rhombus sums before adding them to the final list, then sort to ensure uniqueness is maintained.
Edge case where no rhombus can be formed (e.g., 1x2 grid).	The solution should still treat each individual cell as a rhombus of size 0 and return up to 3 unique values from the grid.