Grid Illumination #10 Most Asked
HardThere is a 2D grid of size n x n where each cell of this grid has a lamp that is initially turned off.
You are given a 2D array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. Even if the same lamp is listed more than once, it is turned on.
When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.
You are also given another 2D array queries, where queries[j] = [rowj, colj]. For the jth query, determine whether grid[rowj][colj] is illuminated or not. After answering the jth query, turn off the lamp at grid[rowj][colj] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowj][colj].
Return an array of integers ans, where ans[j] should be 1 if the cell in the jth query was illuminated, or 0 if the lamp was not.
Example 1:
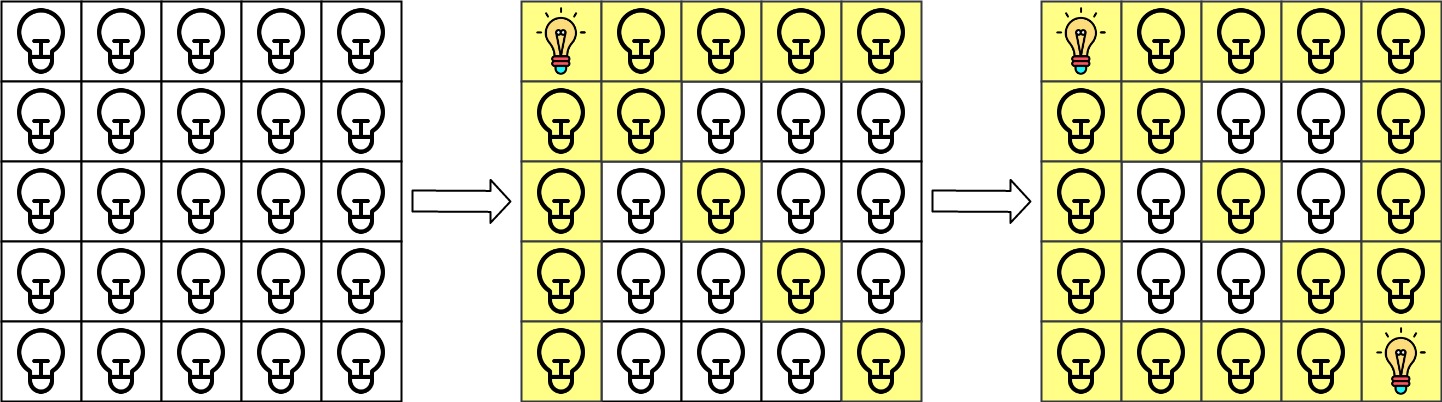
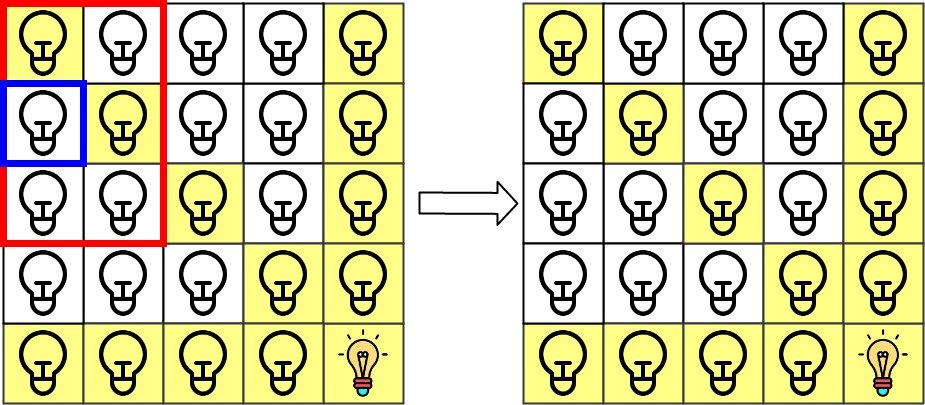
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]] Output: [1,0] Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4]. The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.
Example 2:
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]] Output: [1,1]
Example 3:
Input: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]] Output: [1,1,0]
Constraints:
1 <= n <= 1090 <= lamps.length <= 200000 <= queries.length <= 20000lamps[i].length == 20 <= rowi, coli < nqueries[j].length == 20 <= rowj, colj < n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (n x n), and what is the maximum possible value for 'n'?
- What are the possible ranges for the row and column values in the 'lamps' and 'queries' arrays? Can they be negative?
- If a query point is illuminated by multiple lamps, should the response indicate how many lamps illuminate it, or just that it is illuminated (1)?
- If a lamp is already off (because it was turned off by a previous query), and the same lamp is included again in the lamps array, should it be considered on or off?
- Are the row and column values 0-indexed, or 1-indexed?
Brute Force Solution
Approach
Imagine a grid where light bulbs are placed and you want to know which cells are lit. The brute force approach is to manually check every cell in the grid after each action, considering all light bulbs and how they illuminate.
Here's how the algorithm would work step-by-step:
- First, place all the light bulbs on the grid according to their given locations.
- When asked if a particular cell is lit, painstakingly check if any of the light bulbs illuminate that cell, remembering that each light bulb illuminates its row, column, and both diagonals.
- To check if a cell is lit, go through each light bulb one by one.
- For each light bulb, determine if the cell in question is on the same row, same column, or either of the diagonals as the light bulb.
- If the cell is on the same row, column, or diagonal as any light bulb, then the cell is lit.
- After determining if the cell is lit or not, record the result.
- When a light bulb is turned off, remove that light bulb from its location.
- Repeat this whole process every time you want to check if a cell is lit, considering the current placement of all the remaining light bulbs.
Code Implementation
def grid_illumination_brute_force(grid_size, lamps, queries):
illuminated_cells_results = []
lamp_positions = set(tuple(lamp) for lamp in lamps)
for query in queries:
row_query, column_query = query
is_illuminated = False
# Iterate through all lamps to check if they illuminate the cell.
for row_lamp, column_lamp in lamp_positions:
if (row_lamp == row_query or \
column_lamp == column_query or \
abs(row_lamp - row_query) == abs(column_lamp - column_query)):
is_illuminated = True
break
illuminated_cells_results.append(1 if is_illuminated else 0)
# Turn off lamps adjacent to the query cell.
for row_offset in range(-1, 2):
for column_offset in range(-1, 2):
row_to_remove = row_query + row_offset
column_to_remove = column_query + column_offset
if 0 <= row_to_remove < grid_size and 0 <= column_to_remove < grid_size:
lamp_to_remove = (row_to_remove, column_to_remove)
# Check for if the lamps exist, and remove
if lamp_to_remove in lamp_positions:
lamp_positions.remove(lamp_to_remove)
return illuminated_cells_resultsBig(O) Analysis
Optimal Solution
Approach
The key is to avoid checking every single cell in the grid repeatedly. Instead, we use memory to keep track of which rows, columns, and diagonals are lit, and quickly determine if a query point is illuminated.
Here's how the algorithm would work step-by-step:
- First, think about how the lamps light up the grid. Each lamp illuminates its entire row and column, plus both diagonals.
- Instead of physically lighting up the grid, we will keep a count of how many lamps are lighting up each row, column, and diagonal.
- Use separate counters for rows, columns, and the two types of diagonals. We can identify each diagonal by a simple formula involving the row and column numbers.
- When you place a lamp, increase the counts for its row, column, and diagonals.
- When a lamp is extinguished, decrease the counts for its row, column, and diagonals. Be careful not to extinguish a lamp that isn't there.
- To check if a cell is lit, simply look at the counts for its row, column, and the two diagonals it belongs to. If any of those counts are greater than zero, the cell is lit.
- For each query, check the cell and its immediate neighbors (8 neighbors plus itself). Extinguish any lamps in those 9 locations. It is important to note that you must remove lamps from the lamp locations and decrement the counts only once. This can be done using a set or a dictionary.
- After checking a query and potentially extinguishing lamps, record whether the original query location was lit before moving on to the next query.
Code Implementation
def grid_illumination(grid_size, lamps, queries):
row_counts = {}
column_counts = {}
diagonal_counts = {}
anti_diagonal_counts = {}
lamp_positions = set()
for row, col in lamps:
if (row, col) in lamp_positions:
continue
lamp_positions.add((row, col))
row_counts[row] = row_counts.get(row, 0) + 1
column_counts[col] = column_counts.get(col, 0) + 1
diagonal = row - col
diagonal_counts[diagonal] = diagonal_counts.get(diagonal, 0) + 1
anti_diagonal = row + col
anti_diagonal_counts[anti_diagonal] = anti_diagonal_counts.get(anti_diagonal, 0) + 1
results = []
for row, col in queries:
is_illuminated = False
if row_counts.get(row, 0) > 0 or \
column_counts.get(col, 0) > 0 or \
diagonal_counts.get(row - col, 0) > 0 or \
anti_diagonal_counts.get(row + col, 0) > 0:
is_illuminated = True
results.append(is_illuminated)
# Iterate through neighbors and the cell itself.
for neighbor_row in range(max(0, row - 1), min(grid_size, row + 2)):
for neighbor_col in range(max(0, col - 1), min(grid_size, col + 2)):
# Extinguish lamps in the neighbors.
if (neighbor_row, neighbor_col) in lamp_positions:
# Decrement counts ONLY if a lamp exists at that spot.
lamp_positions.remove((neighbor_row, neighbor_col))
row_counts[neighbor_row] -= 1
column_counts[neighbor_col] -= 1
diagonal = neighbor_row - neighbor_col
diagonal_counts[diagonal] -= 1
anti_diagonal = neighbor_row + neighbor_col
anti_diagonal_counts[anti_diagonal] -= 1
# Clean up zero counts, preventing negative values.
if row_counts[neighbor_row] == 0:
del row_counts[neighbor_row]
if column_counts[neighbor_col] == 0:
del column_counts[neighbor_col]
if diagonal_counts[diagonal] == 0:
del diagonal_counts[diagonal]
if anti_diagonal_counts[anti_diagonal] == 0:
del anti_diagonal_counts[anti_diagonal]
return resultsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty grid (n=0) or no lamps | Return an empty result array immediately as there are no illuminated cells or queries to process. |
| Large grid size (n approaching integer limit) with many lamps | Use hash maps (dictionaries) instead of a full grid representation to manage memory efficiently and prevent overflow. |
| Lamp coordinates outside the grid boundaries (r < 0, c < 0, r >= n, c >= n) | Filter out such lamp coordinates before adding them to the lamp tracking structures to prevent out-of-bounds access. |
| Duplicate lamp coordinates (multiple lamps at the same position) | The algorithm should correctly handle duplicate lamp coordinates by overwriting the existing lamp in the relevant data structures and not double-counting the illumination. |
| Query coordinates outside the grid boundaries | Return 0 for these queries, as they're not within the valid illuminated space. |
| Integer overflow when calculating illuminated regions or neighbor coordinates | Utilize appropriate data types (e.g., long integers) to prevent overflow when calculating grid positions or illuminated regions. |
| No lamps are lit initially | The queries should all return 0 as the grid is initially unlit. |
| All lamps are lit initially | Queries should all return 1 until a lamp is turned off; ensure turn-off logic is correct. |