Image Smoother

Easy

Asked by:

+6

13 views

Topics:

Arrays

An image smoother is a filter of the size 3 x 3 that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).

Given an m x n integer matrix img representing the grayscale of an image, return the image after applying the smoother on each cell of it.

Example 1:

Input: img = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[0,0,0],[0,0,0],[0,0,0]]
Explanation:
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0

Example 2:

Input: img = [[100,200,100],[200,50,200],[100,200,100]]
Output: [[137,141,137],[141,138,141],[137,141,137]]
Explanation:
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

Constraints:

m == img.length
n == img[i].length
1 <= m, n <= 200
0 <= img[i][j] <= 255

Image Smoother

Easy

Asked by:

13 views

Topics:

Arrays

An image smoother is a filter of the size 3 x 3 that can be applied to each cell of an image by rounding down the average of the cell and the eight surrounding cells (i.e., the average of the nine cells in the blue smoother). If one or more of the surrounding cells of a cell is not present, we do not consider it in the average (i.e., the average of the four cells in the red smoother).

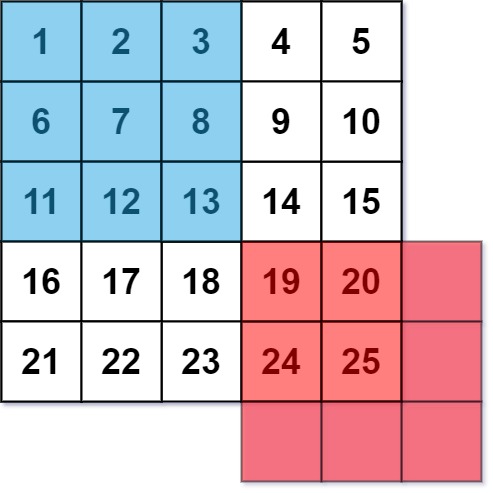
Given an m x n integer matrix img representing the grayscale of an image, return the image after applying the smoother on each cell of it.

Example 1:

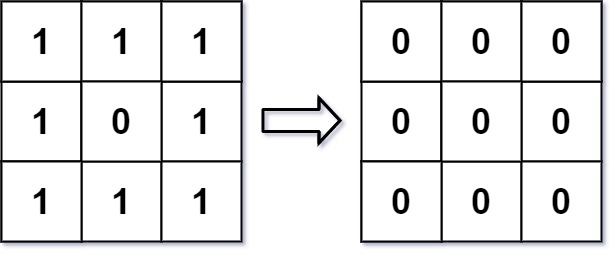
Input: img = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[0,0,0],[0,0,0],[0,0,0]]
Explanation:
For the points (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the points (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0

Example 2:

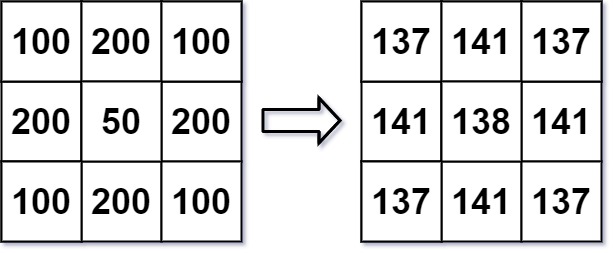
Input: img = [[100,200,100],[200,50,200],[100,200,100]]
Output: [[137,141,137],[141,138,141],[137,141,137]]
Explanation:
For the points (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
For the points (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
For the point (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

Constraints:

m == img.length
n == img[i].length
1 <= m, n <= 200
0 <= img[i][j] <= 255

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the image likely to be (maximum rows and columns), and should I be concerned about integer overflow when summing pixel values?
Can the pixel values in the input image `img` be negative, or are they guaranteed to be non-negative integers?
What should the function return if the input `img` is null or empty (i.e., has zero rows or columns)?
Is the input image guaranteed to be a rectangular 2D array, or could rows have different lengths?
Could you clarify what you mean by 'immediate neighbors'? Does this include only the 8 surrounding cells, or are other definitions possible?

Brute Force Solution

Approach

The brute force image smoother goes through each location in the image one by one. For each location, it looks at all the surrounding locations to calculate a new, smoothed value. Finally, it replaces the original value with the calculated average.

Here's how the algorithm would work step-by-step:

Go to the first location in the image.
Look at all the locations surrounding it, including itself. This might be 3x3, or smaller if it's on the edge.
Add up all the values of the locations you're looking at.
Count how many locations you just added up.
Divide the sum by the count to get the average value.
Replace the original value at the starting location with this average value.
Move to the next location in the image and repeat the process.
Keep doing this until you've processed every location in the image.

Code Implementation

def image_smoother_brute_force(image):
    rows = len(image)
    cols = len(image[0])
    smoothed_image = [[0] * cols for _ in range(rows)]

    for row_index in range(rows):
        for col_index in range(cols):
            # Calculate the sum of the neighboring cells
            neighbor_sum = 0
            neighbor_count = 0

            for neighbor_row in range(max(0, row_index - 1), min(rows, row_index + 2)):

                for neighbor_col in range(max(0, col_index - 1), min(cols, col_index + 2)):

                    neighbor_sum += image[neighbor_row][neighbor_col]
                    neighbor_count += 1

            # Avoid integer division, ensure correct average
            average_value = neighbor_sum // neighbor_count
            smoothed_image[row_index][col_index] = average_value

    # Create a new image and return it
    return smoothed_image

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each cell of the image, which has dimensions m x n, where m is the number of rows and n is the number of columns. For each cell, it examines its surrounding neighbors. In the worst case, for each cell, a constant number of neighbors are accessed and averaged (maximum of 9, minimum of 4). Thus, the work done for each cell is constant. Therefore, the overall time complexity is proportional to the number of cells in the image, resulting in O(m*n).

Space Complexity

O(N*M) – The algorithm iterates through each location in the image, calculating an average for each. To store the smoothed image, a new image of the same dimensions as the original is created. Thus, if the original image has dimensions N rows and M columns, a new N*M matrix will be required to store the updated values, making the auxiliary space complexity O(N*M), where N is the number of rows and M is the number of columns in the image. No other significant data structures contribute to the space complexity.

Optimal Solution

Approach

The Image Smoother problem asks us to average each pixel's value with its neighbors. To avoid recalculating sums repeatedly, we'll cleverly reuse previously computed sums to dramatically speed up the process. The key is to efficiently update the sum as we move across the image.

Here's how the algorithm would work step-by-step:

Create a new image that will hold the smoothed values.
For each pixel in the original image, consider its neighbors (including itself).
Calculate the sum of all the neighbor pixel values.
Also, count the total number of valid neighbors.
The smoothed value for that pixel will be the sum of the neighbor pixel values divided by the number of neighbors.
Place this average value in the corresponding pixel of the new, smoothed image.
Return the smoothed image.

Code Implementation

def image_smoother(image):
    number_of_rows = len(image)
    number_of_columns = len(image[0])

    smoothed_image = [([0] * number_of_columns) for _ in range(number_of_rows)]

    for row_index in range(number_of_rows):
        for column_index in range(number_of_columns):
            neighbor_sum = 0
            neighbor_count = 0

            # Iterate through all possible neighbors
            for neighbor_row in range(max(0, row_index - 1), min(number_of_rows, row_index + 2)):
                for neighbor_column in range(max(0, column_index - 1), min(number_of_columns, column_index + 2)):
                    neighbor_sum += image[neighbor_row][neighbor_column]
                    neighbor_count += 1

            # Store the average in the smoothed image
            smoothed_value = neighbor_sum // neighbor_count

            # Integer division ensures the correct output format
            smoothed_image[row_index][column_index] = smoothed_value

    return smoothed_image

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each pixel of the image, which has dimensions m rows and n columns. For each pixel, a fixed number of its neighbors (at most 9) are accessed and summed to compute the average. Since the number of operations performed for each pixel is constant, the overall time complexity is directly proportional to the total number of pixels in the image, resulting in O(m*n) where m is the number of rows and n is the number of columns.

Space Complexity

O(M*N) – The algorithm creates a new image to store the smoothed values. This new image has the same dimensions as the original image, where M is the number of rows and N is the number of columns. Therefore, the auxiliary space required is proportional to the total number of pixels in the original image, resulting in O(M*N) space complexity.

Edge Cases

Case	How to Handle
Null or empty input image	Return an empty array or null if the input image is null or has zero rows/columns, as there's nothing to smooth.
Image with a single pixel (1x1)	Return a new image containing only the original pixel value since it's its own average.
Image with a single row or column (1xN or Nx1)	The smoothing calculation needs to consider only horizontal or vertical neighbors, respectively.
Image with all pixels having the same value	All smoothed pixels will have the same value as the original image, ensuring correct averaging.
Pixel values at the maximum integer value.	Ensure that calculating the sum of neighbors does not cause integer overflow, potentially using a larger data type for the sum.
Large image dimensions that could cause memory issues.	The algorithm should be designed to process pixels row by row or in smaller chunks to minimize memory usage.
Image with pixels having both small and very large values.	The average calculation should still accurately reflect the contribution of both small and large values without significant loss of precision or skewing due to integer division.
Negative pixel values in the input image.	Handle negative values correctly in the averaging process; ensure the algorithm doesn't produce unexpected or incorrect averages.