Increasing Order Search Tree
EasyGiven the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:

Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9] Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
Example 2:
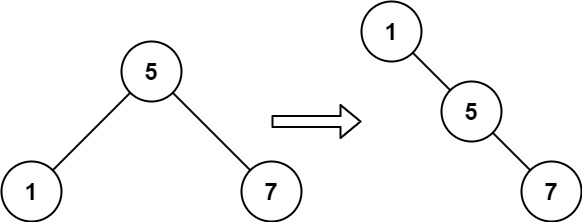
Input: root = [5,1,7] Output: [1,null,5,null,7]
Constraints:
- The number of nodes in the given tree will be in the range
[1, 100]. 0 <= Node.val <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary search tree be empty?
- Are the values in the tree guaranteed to be unique, or could there be duplicates?
- Should the new tree be created in-place, or should I create a new tree and return it?
- Is the input guaranteed to be a valid binary search tree?
- What should I return if the input is null?
Brute Force Solution
Approach
The brute force approach to rearranging a tree into increasing order is like taking all the pieces of a puzzle and trying every possible arrangement until you find the right one. We extract all the values, then rebuild the tree in every conceivable way.
Here's how the algorithm would work step-by-step:
- First, take the tree and gather all the values it contains. Imagine carefully writing down each value in the tree as you find it.
- Then, sort those values in increasing order, like arranging numbers from smallest to largest.
- Now, consider all possible ways to link those sorted values together to form a new tree where each value is greater than the one before it.
- For each possible tree, check if it is valid, making sure each value appears exactly once and that the tree follows all the rules of an increasing order tree.
- Finally, once you've explored all possibilities, pick the one that works. This may be the first one you find, or the only valid one.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def increasing_order_search_tree_brute_force(root):
all_values = []
def inorder_traversal(node):
if node:
inorder_traversal(node.left)
all_values.append(node.value)
inorder_traversal(node.right)
inorder_traversal(root)
all_values.sort()
# This function generates all possible right-skewed trees
def generate_trees(values):
if not values:
return [None]
trees = []
# We only need to consider creating right-skewed trees
new_root = TreeNode(values[0])
current_node = new_root
for i in range(1, len(values)):
current_node.right = TreeNode(values[i])
current_node = current_node.right
trees.append(new_root)
return trees
# Generate all possible trees from sorted values
possible_trees = generate_trees(all_values)
# Check if a tree is a valid increasing order tree
def is_valid_increasing_tree(root_node, values_list):
current_node = root_node
index = 0
while current_node:
if current_node.value != values_list[index]:
return False
current_node = current_node.right
index += 1
if index != len(values_list):
return False
return True
# Iterate through all trees and return first valid one
for tree in possible_trees:
if is_valid_increasing_tree(tree, all_values):
# Return the first valid tree
return tree
return NoneBig(O) Analysis
Optimal Solution
Approach
We want to rearrange the tree so that it looks like a linked list that is ordered from smallest to largest. The core idea is to traverse the tree in a special order that naturally produces the sorted arrangement as we go. We build the new tree piece by piece as we visit each element.
Here's how the algorithm would work step-by-step:
- Start by figuring out what the smallest element in the entire tree is; that's where our new tree will begin.
- As we move through the original tree from smallest element to next largest element, we build the new sorted tree by connecting each element to the previous one.
- Essentially, as we find the next smallest element, we attach it to the right side of the last element we added to our new tree.
- After we've processed every element in the original tree, the result is a linked-list shaped tree that has all the elements in increasing order, exactly as desired.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def increasingBST(self, root):
def inorder_traversal(node):
if not node:
return
inorder_traversal(node.left)
nonlocal current_node
current_node.right = TreeNode(node.val)
current_node = current_node.right
inorder_traversal(node.right)
# Dummy node starts the new tree.
dummy_node = TreeNode(0)
current_node = dummy_node
# Inorder traversal to visit nodes in ascending order.
inorder_traversal(root)
# Return the new tree, skipping the dummy node.
return dummy_node.rightBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree input | Return null or an empty tree (depending on requirements) if the root is null, indicating an empty tree. |
| Single node tree | Return a new tree with only that single node as both the root and the right child, and null left child. |
| Tree with all nodes having the same value | The in-order traversal will produce a chain of nodes with the same value, handled correctly by standard in-order traversal. |
| Completely skewed tree (left or right) | The in-order traversal will still correctly flatten the tree into increasing order, although the recursion depth might be larger. |
| Tree with duplicate values | The in-order traversal will handle duplicates correctly, placing them in the order they are visited during the traversal. |
| Very large tree (potential stack overflow with recursion) | Consider iterative in-order traversal using a stack to avoid potential stack overflow issues with deep recursion. |
| Tree with negative or zero values | The algorithm should work correctly with negative or zero values as the in-order traversal only depends on the relative order of nodes. |
| Integer overflow in extremely large tree height when managing right pointers | Ensure that memory allocation and pointer manipulation are handled carefully to prevent memory leaks or corruption, especially with large trees. |