Increment Submatrices by One

Medium

Adobe

0 views

Topics:

Arrays

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1_i, col1_i, row2_i, col2_i], you should do the following operation:

Add 1 to every element in the submatrix with the top left corner (row1_i, col1_i) and the bottom right corner (row2_i, col2_i). That is, add 1 to mat[x][y] for all row1_i <= x <= row2_i and col1_i <= y <= col2_i.

Return the matrix mat after performing every query.

Example 1:

Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

Constraints:

1 <= n <= 500
1 <= queries.length <= 10⁴
0 <= row1_i <= row2_i < n
0 <= col1_i <= col2_i < n

Increment Submatrices by One

Medium

Adobe

0 views

Topics:

Arrays

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1_i, col1_i, row2_i, col2_i], you should do the following operation:

Add 1 to every element in the submatrix with the top left corner (row1_i, col1_i) and the bottom right corner (row2_i, col2_i). That is, add 1 to mat[x][y] for all row1_i <= x <= row2_i and col1_i <= y <= col2_i.

Return the matrix mat after performing every query.

Example 1:

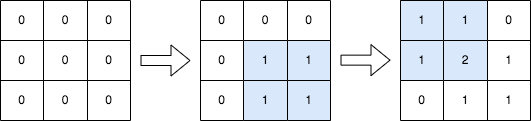
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

Constraints:

1 <= n <= 500
1 <= queries.length <= 10⁴
0 <= row1_i <= row2_i < n
0 <= col1_i <= col2_i < n

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the size of 'n' and the number of queries? Specifically, what is the maximum possible value for 'n' and the number of queries in the 'queries' list?
Are row1, col1, row2, and col2 guaranteed to be within the bounds of the n x n matrix (i.e., between 0 and n-1 inclusive)? What should I do if a query has invalid coordinates?
Are row1 <= row2 and col1 <= col2 always guaranteed? If not, how should I handle cases where row1 > row2 or col1 > col2?
Should the output matrix be a new matrix or can I modify the input matrix in-place? (If the input is given).
What data type should I use for the matrix elements to handle potential overflow if many increments are performed? Can I assume integer data types, or might I need to consider using long/BigInteger?

Brute Force Solution

Approach

The brute force approach to this problem means going through each instruction one at a time and directly applying it to the grid. We essentially simulate each increment operation without trying to be clever or optimize anything. We update the grid exactly as the instructions tell us to.

Here's how the algorithm would work step-by-step:

Take the first set of coordinates that describe the top-left and bottom-right corners of a submatrix.
Go to the grid and, for every cell located within those coordinates, increase its value by one.
Repeat this process for the second set of coordinates, increasing all the values in that submatrix by one as well.
Continue this process, one set of coordinates at a time, until you've handled every single set of coordinates and incremented the corresponding submatrices.
The final updated grid is then the result.

Code Implementation

def increment_submatrices_by_one(grid, instructions):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    # Iterate through each instruction to update the grid
    for instruction in instructions:
        top_row, left_column, bottom_row, right_column = instruction

        # Iterate through the specified submatrix
        for row_index in range(top_row, bottom_row + 1):

            # Iterate through the columns of the current row
            for column_index in range(left_column, right_column + 1):

                # Increment the cell by one
                grid[row_index][column_index] += 1

    return grid

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n * k) – Let 'm' and 'n' denote the dimensions of the grid (rows and columns, respectively), and let 'k' be the number of increment operations (i.e., the number of submatrices to increment). For each of the 'k' operations, we iterate through the specified submatrix. In the worst case, each submatrix could span the entire grid, requiring us to visit all 'm * n' cells to increment them by one. Therefore, the time complexity is O(m * n * k).

Space Complexity

O(1) – The provided solution operates directly on the input grid and the instructions, modifying the grid in place. It does not create any auxiliary data structures like temporary arrays, lists, or hash maps to store intermediate results. The only extra memory used would be a few variables to store the row and column indices during the increment operation, which takes constant space regardless of the size of the grid or the number of instructions. Therefore, the auxiliary space complexity is O(1).

Optimal Solution

Approach

The efficient approach avoids directly updating all the numbers in each specified area. Instead, it cleverly records how many times each corner of the grid is affected and then calculates the overall effect later.

Here's how the algorithm would work step-by-step:

For each submatrix we need to increment, mark its top-left corner with a positive one (+1).
Mark the cells just outside the bottom-right corner of the submatrix with a positive one (+1) and a negative one (-1) for the corners just outside the top-right and bottom-left corners.
After marking all the corners for all submatrices, go through the grid, adding up the values from the top and the left to each cell. This will give you the total increase each cell should have.
The final grid will contain the result of all the requested increment operations.

Code Implementation

def increment_submatrices_by_one(grid_rows, grid_cols, updates):
    difference_matrix = [[0] * grid_cols for _ in range(grid_rows)]

    for top_row, left_col, bottom_row, right_col in updates:
        # Mark the top-left corner with +1.
        difference_matrix[top_row][left_col] += 1

        if bottom_row + 1 < grid_rows:
            # Mark the cell below the bottom-right corner with -1.
            difference_matrix[bottom_row + 1][left_col] -= 1

        if right_col + 1 < grid_cols:
            # Mark the cell to the right of the top-right corner with -1.
            difference_matrix[top_row][right_col + 1] -= 1

        if bottom_row + 1 < grid_rows and right_col + 1 < grid_cols:
            difference_matrix[bottom_row + 1][right_col + 1] += 1

    # Accumulate values to get the incremented matrix.
    result_matrix = [[0] * grid_cols for _ in range(grid_rows)]
    for row_index in range(grid_rows):
        for col_index in range(grid_cols):
            if row_index == 0 and col_index == 0:
                result_matrix[row_index][col_index] = difference_matrix[row_index][col_index]
            elif row_index == 0:
                # Propagate values from the left.
                result_matrix[row_index][col_index] = result_matrix[row_index][col_index - 1] + difference_matrix[row_index][col_index]
            elif col_index == 0:
                # Propagate values from above.
                result_matrix[row_index][col_index] = result_matrix[row_index - 1][col_index] + difference_matrix[row_index][col_index]
            else:
                # Accumulate values from top and left, subtracting the overlap.
                result_matrix[row_index][col_index] = result_matrix[row_index - 1][col_index] + result_matrix[row_index][col_index - 1] - result_matrix[row_index - 1][col_index - 1] + difference_matrix[row_index][col_index]

    return result_matrix

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n*n) – The algorithm iterates through the list of submatrices to increment. The time complexity to mark the corners is O(m) where m is the number of increment operations. After marking all the corners, the algorithm iterates through each cell in the n x n grid once to compute the final result. Therefore the time complexity of the final step is O(n*n). Considering both steps, the dominant term is O(n*n), therefore the total time complexity is O(n*n).

Space Complexity

O(1) – The algorithm primarily modifies the input grid in place. The corner markings (+1 and -1) are directly applied to the existing grid structure, so it doesn't create any significant auxiliary data structures. Therefore, the space complexity is dominated by a few integer variables for iterating through the grid and doesn't scale with the size of the input. Thus the space complexity is constant.

Edge Cases

Case	How to Handle
n is zero or negative	Return an empty matrix or raise an IllegalArgumentException as a matrix with zero or negative dimensions is invalid.
queries is null or empty	Return a matrix of size n x n filled with zeros, as no updates are needed.
row1, col1, row2, or col2 are out of bounds (less than 0 or greater than or equal to n)	Handle by either skipping the invalid query, clamping the values to the valid range [0, n-1], or throwing an IllegalArgumentException for invalid input.
row1 > row2 or col1 > col2	Treat the submatrix as empty, skipping the increment operation for that particular query.
n is a very large number (potential memory issues)	Consider using a sparse matrix representation or other memory-efficient data structures if n is extremely large and memory is a constraint.
Large number of queries	The solution should iterate efficiently over the queries without excessive overhead; consider algorithm optimization for performance.
Integer overflow if increments are very large or there are many queries on the same submatrix.	Use a larger integer type (e.g., long) to prevent integer overflow during the increment operation or handle overflow errors explicitly.
All queries represent the entire matrix	The matrix will be incremented by the number of queries across all of its elements and should still produce a valid n x n result.