Insert into a Binary Search Tree
MediumYou are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.
Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.
Example 1:

Input: root = [4,2,7,1,3], val = 5 Output: [4,2,7,1,3,5] Explanation: Another accepted tree is: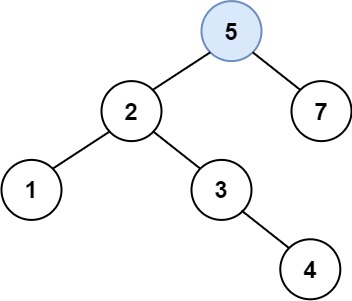
Example 2:
Input: root = [40,20,60,10,30,50,70], val = 25 Output: [40,20,60,10,30,50,70,null,null,25]
Example 3:
Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 Output: [4,2,7,1,3,5]
Constraints:
- The number of nodes in the tree will be in the range
[0, 104]. -108 <= Node.val <= 108- All the values
Node.valare unique. -108 <= val <= 108- It's guaranteed that
valdoes not exist in the original BST.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data type of the node values? Are they integers, floats, or something else, and what is the possible range of values?
- If the value to be inserted is already present in the BST, should I insert it as a duplicate, or should the tree remain unchanged?
- Should the function return the root of the modified tree, or is modifying the tree in-place sufficient?
- What should I return if the root node is null, indicating an empty tree to begin with?
- Are there any specific balance requirements for the BST after the insertion (e.g., should it remain a balanced BST)?
Brute Force Solution
Approach
The brute force method to insert a value into a binary search tree involves exploring all possible locations until we find the right spot. We essentially walk through the tree, comparing the new value with each existing node, and checking at each step if we can insert it directly.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root.
- Compare the value we want to insert with the value at the current node.
- If the new value is smaller, look at the node to the left. If there's no node to the left, then this is where the new value goes; we've found our spot.
- If the new value is larger, look at the node to the right. If there's no node to the right, then this is where the new value goes; we've found our spot.
- If we haven't found a spot, keep repeating the comparison process, moving left or right as needed until we reach a point where there's no node in the direction we need to go.
Code Implementation
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
new_node = Node(value)
if self.root is None:
self.root = new_node
return
current_node = self.root
while True:
if value < current_node.value:
# Move to the left if the value is smaller.
if current_node.left is None:
current_node.left = new_node
return
current_node = current_node.left
else:
# Move to the right if the value is larger or equal.
if current_node.right is None:
current_node.right = new_node
return
current_node = current_node.rightBig(O) Analysis
Optimal Solution
Approach
We want to add a new value to the correct spot in a special tree where the values are ordered. To do this efficiently, we'll follow the tree's structure and only look at the relevant parts, making sure the tree stays properly organized.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, which is called the root.
- Compare the value you want to add with the value at the current spot.
- If the new value is smaller, go down to the left side of the tree.
- If the new value is bigger, go down to the right side of the tree.
- Keep going down, making these left or right choices, until you reach an empty spot where there's no tree yet.
- When you find this empty spot, put the new value there.
- You've now added the value in the right place, and the tree is still organized correctly.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def insert_into_bst(root_node, value_to_insert):
if not root_node:
return TreeNode(value_to_insert)
current_node = root_node
while True:
if value_to_insert < current_node.value:
# Traverse left if new value is less.
if current_node.left is None:
current_node.left = TreeNode(value_to_insert)
return root_node
current_node = current_node.left
else:
# Traverse right if new value is greater or equal.
if current_node.right is None:
# Insert the new node at the empty right child.
current_node.right = TreeNode(value_to_insert)
return root_node
current_node = current_node.rightBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Root is null (empty tree) | Create a new tree with the inserted node as the root if the root is null. |
| Value already exists in the tree (duplicates) | Define behavior: either insert to the left/right (maintaining BST property) or do not insert at all based on problem specifications; commonly don't insert. |
| Inserting at the root | Handles correctly by traversing down the tree until an appropriate insertion point is found which may immediately be the root. |
| Large, skewed tree (e.g., all values inserted in increasing order) | Ensure the algorithm maintains a balanced tree structure if required (e.g., AVL, Red-Black) or recursion depth may cause a stack overflow; iterative solutions are preferred for very large, unbalanced trees. |
| Inserting a value smaller than the smallest value in the tree | The algorithm will correctly traverse to the leftmost node and insert it as the new leftmost child. |
| Inserting a value larger than the largest value in the tree | The algorithm will correctly traverse to the rightmost node and insert it as the new rightmost child. |
| Integer overflow potential when comparing values | Use appropriate data types to prevent overflow, and be mindful of languages where implicit casts might occur during comparison. |
| Deeply unbalanced tree and recursion depth limits | Consider iterative solution to avoid stack overflow in cases of deeply unbalanced trees. |