Interleaving String

Medium

Nuro

2 views

Topics:

StringsDynamic Programming

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

s = s₁ + s₂ + ... + s_n
t = t₁ + t₂ + ... + t_m
|n - m| <= 1
The interleaving is s₁ + t₁ + s₂ + t₂ + s₃ + t₃ + ... or t₁ + s₁ + t₂ + s₂ + t₃ + s₃ + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a".
Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac".
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Interleaving String

Medium

Nuro

2 views

Topics:

StringsDynamic Programming

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

s = s₁ + s₂ + ... + s_n
t = t₁ + t₂ + ... + t_m
|n - m| <= 1
The interleaving is s₁ + t₁ + s₂ + t₂ + s₃ + t₃ + ... or t₁ + s₁ + t₂ + s₂ + t₃ + s₃ + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

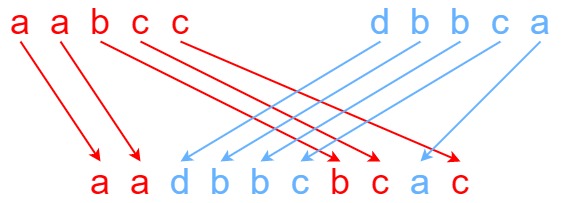
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a".
Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac".
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

0 <= s1.length, s2.length <= 100
0 <= s3.length <= 200
s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the input strings s1, s2, and s3 be null or empty?
Are there any constraints on the lengths of s1, s2, and s3? What is the maximum length I should expect?
Is it guaranteed that the length of s3 will always be the sum of the lengths of s1 and s2?
Are the input strings composed of only ASCII characters, or should I consider Unicode characters?
If s3 cannot be formed by interleaving s1 and s2, what should I return? Should I return `false`, throw an exception, or something else?

Brute Force Solution

Approach

The brute force approach to checking if one string is an interleaving of two other strings is like trying every single way to merge those two strings together. We explore every possible combination of characters from each of the two strings to see if any of them match the third string.

Here's how the algorithm would work step-by-step:

Start by taking a character from the first string.
Then, take a character from the second string.
Keep alternating between taking characters from the first and second strings in every possible order.
Each time you take a character, build a new combined string.
After you have combined all characters from both strings, check if the combined string exactly matches the third string.
If it matches, you've found a valid interleaving, and the answer is yes.
If you have tried all possible combinations of taking characters from the first and second strings, and none of them match the third string, then the answer is no.

Code Implementation

def is_interleave_brute_force(first_string, second_string, combined_string):
    def solve(first_string_index, second_string_index, current_string):
        # If we've used all characters from both strings
        if first_string_index == len(first_string) and second_string_index == len(second_string):
            return current_string == combined_string

        # Try taking a character from the first string
        if first_string_index < len(first_string):
            if solve(first_string_index + 1, second_string_index, current_string + first_string[first_string_index]):
                return True

        # Try taking a character from the second string
        if second_string_index < len(second_string):
            if solve(first_string_index, second_string_index + 1, current_string + second_string[second_string_index]):
                return True

        return False

    # Start the recursive process
    return solve(0, 0, "")

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The brute force approach explores all possible interleavings of two strings of length m and n respectively. In the worst case, each character from either string a or string b can be chosen at each step to form the interleaved string. This leads to a branching factor of 2 for each of the m+n characters to be chosen, resulting in a decision tree with approximately 2^(m+n) leaves. Each leaf represents a potential interleaving that needs to be checked. Therefore, the time complexity is O(2^(m+n)).

Space Complexity

O(2^(m+n)) – The brute force approach explores all possible interleavings by recursively building combined strings. In the worst case, we explore every combination of characters from the first string (length m) and the second string (length n). The depth of the recursion tree can be m+n, and at each level, multiple branches are created, resulting in potentially exploring a large number of paths, specifically up to 2^(m+n) in the worst-case scenario. Therefore, the space complexity, primarily due to the recursion stack, is exponential, approximating O(2^(m+n)), where m and n are the lengths of the input strings.

Optimal Solution

Approach

We need to figure out if a third string can be formed by mixing the characters from two other strings. The trick is to see if we can build the third string piece by piece, choosing characters from the first or second string, without getting stuck or making any impossible choices.

Here's how the algorithm would work step-by-step:

Imagine you're building the third string one character at a time.
At each step, you have a choice: take the next character from the first string, or the next character from the second string.
Keep track of whether you can reach a specific point in the third string using some combination of characters from the first two strings.
If you can reach the end of the third string by making valid choices from the first two strings, then the third string is indeed an interleaving of the other two.
If you ever reach a point where neither the first nor the second string can provide the next character to match the third string, then it's not possible.

Code Implementation

def is_interleave(first_string, second_string, third_string):
    first_string_length = len(first_string)
    second_string_length = len(second_string)
    third_string_length = len(third_string)

    if first_string_length + second_string_length != third_string_length:
        return False

    # dp[i][j] is True if third_string[0...i+j-1] is formed by
    # interleaving first_string[0...i-1] and second_string[0...j-1]
    dp_table = [[False] * (second_string_length + 1) for _ in range(first_string_length + 1)]

    # Base case: Empty strings interleave to form an empty string
    dp_table[0][0] = True

    # Fill the DP table in bottom-up manner
    for i in range(first_string_length + 1):
        for j in range(second_string_length + 1):
            if i > 0:
                # Check if current char of first_string matches and previous state is True
                if first_string[i - 1] == third_string[i + j - 1] and dp_table[i - 1][j]:

                    dp_table[i][j] = True

            if j > 0:
                # Check if current char of second_string matches and previous state is True
                if second_string[j - 1] == third_string[i + j - 1] and dp_table[i][j - 1]:

                    dp_table[i][j] = True

    # If the last cell is True, then the strings are interleaved
    return dp_table[first_string_length][second_string_length]

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m * n) – The core of the solution involves exploring all possible combinations of characters from the first two strings (s1 and s2) to construct the third string (s3). We are essentially filling out a 2D DP table of size (m+1)x(n+1) where m is the length of s1 and n is the length of s2. Each cell dp[i][j] represents whether the first i characters of s1 and the first j characters of s2 can interleave to form the first i+j characters of s3. Filling each cell in the table takes constant time O(1). Thus, the time complexity is proportional to the size of the DP table, resulting in O(m * n).

Space Complexity

O(m * n) – The plain English explanation implies using a dynamic programming approach to keep track of whether specific points in the third string can be reached using combinations from the first two strings. This suggests using a 2D array (or similar data structure) where the dimensions are related to the lengths of the first two strings. Specifically, if the first string has length m and the second string has length n, then the algorithm might use a table of size m x n to store intermediate results indicating whether the first i characters of string one and the first j characters of string two can form the first (i+j) characters of string three. Therefore, the auxiliary space used is proportional to the product of the lengths of the two input strings. This yields a space complexity of O(m * n).

Edge Cases

Case	How to Handle
One or both input strings are null or empty.	Return true only if the third string is also null or empty, or handle appropriately based on the problem's requirements if only some are null or empty.
The length of the third string does not equal the sum of the lengths of the first two strings.	Return false immediately as no interleaving is possible.
Very long input strings (close to memory limits) leading to potential stack overflow with recursive solutions or memory issues with DP solutions.	Implement a dynamic programming solution with memoization or tabulation using bottom-up approach for avoiding stack overflow and optimize memory usage.
Strings s1 and s2 are identical and combine to form s3	The solution should correctly identify this as an interleaving without incorrectly using same characters from s1 or s2 twice.
s3 contains characters not present in s1 or s2	Return false since s3 cannot be formed by interleaving s1 and s2.
One of the input strings is significantly longer than the other (e.g., \|s1\| >> \|s2\|).	Ensure that the algorithm does not have worst-case performance depending heavily on the length of the longer string.
When s1 and s2 are very similar to s3, but a character is out of order.	The solution should return false, as only exact interleaving is permitted.
The first character of s1 and s2 are the same, but only one creates a viable path	Backtracking with memoization should correctly check both paths when first characters match and choose the correct one.