Interval List Intersections

Medium

Nuro

0 views

Topics:

ArraysTwo Pointers

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [start_i, end_i] and secondList[j] = [start_j, end_j]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Constraints:

0 <= firstList.length, secondList.length <= 1000
firstList.length + secondList.length >= 1
0 <= start_i < end_i <= 10⁹
end_i < start_i+1
0 <= start_j < end_j <= 10⁹
end_j < start_j+1

Interval List Intersections

Medium

Nuro

0 views

Topics:

ArraysTwo Pointers

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [start_i, end_i] and secondList[j] = [start_j, end_j]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

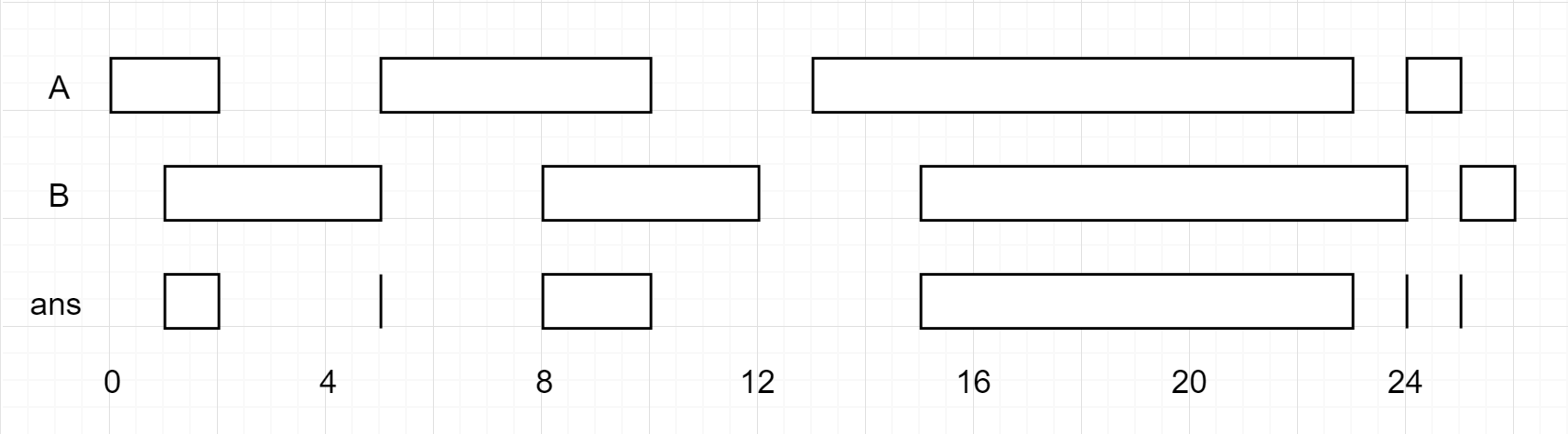
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Constraints:

0 <= firstList.length, secondList.length <= 1000
firstList.length + secondList.length >= 1
0 <= start_i < end_i <= 10⁹
end_i < start_i+1
0 <= start_j < end_j <= 10⁹
end_j < start_j+1

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of values for the start and end points of the intervals in both lists?
Can either `firstList` or `secondList` be empty or null?
If there are no intersections between the two lists, should I return an empty list or null?
Are the intervals within each list guaranteed to be sorted by their start times, or end times, or some other criteria, and are they disjoint?
Could an interval in `firstList` completely encompass an interval in `secondList` or vice versa, and how should the intersection be handled in such cases?

Brute Force Solution

Approach

We have two groups of time slots, and need to find all the times when both groups are busy simultaneously. The brute force approach is like checking every possible pair of time slots, one from each group, to see if they overlap.

Here's how the algorithm would work step-by-step:

Take the very first time slot from the first group.
Compare it with every single time slot from the second group, one at a time.
For each comparison, see if the two time slots overlap at all. If they do, save that overlapping time slot as part of the answer.
Once you've compared the first time slot from the first group with every time slot in the second group, move on to the second time slot in the first group.
Repeat the same comparison process: compare this new time slot with every time slot in the second group, checking for overlaps and saving any overlaps you find.
Keep doing this until you have gone through every single time slot in the first group and compared it with every single time slot in the second group.
The saved overlapping time slots are your final answer.

Code Implementation

def interval_list_intersections_brute_force(first_list, second_list):
    intersection_list = []

    for first_interval in first_list:
        for second_interval in second_list:
            # Check if the intervals overlap
            if (first_interval[1] >= second_interval[0] and
                    second_interval[1] >= first_interval[0]):

                # Determine the start and end of intersection
                intersection_start = max(first_interval[0], second_interval[0])

                # Find the lower end time for the intersection
                intersection_end = min(first_interval[1], second_interval[1])

                # Append the intersection to the result list
                intersection_list.append([intersection_start, intersection_end])

    return intersection_list

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each interval in the first list (let's say it has size m) and, for each of those intervals, compares it against every interval in the second list (let's say it has size n). The overlap check itself takes constant time, O(1). Thus, we have m iterations, each performing n comparisons, leading to a total time complexity of O(m*n).

Space Complexity

O(1) – The provided solution's space complexity is determined by the extra memory it uses beyond the input interval lists. The description mentions saving overlapping time slots as the answer. However, assuming the space to store the answer (the result array of overlapping intervals) does not count towards auxiliary space, the dominant factor is the constant number of variables used for iteration and comparison. Regardless of the size of the input lists, no additional data structures are created whose size scales with the input, meaning that the space usage remains constant. Therefore, the auxiliary space complexity is O(1).

Optimal Solution

Approach

To find the overlapping parts of two lists of time periods, the best way is to go through both lists in order, checking for overlaps as you go. We only need to look at each time period once, making it efficient.

Here's how the algorithm would work step-by-step:

Start with the first time period in each list.
See if those two time periods overlap at all. If they do, record the time that they share.
Figure out which time period ends sooner. The one that ends sooner is 'used up', so move to the next time period in that list.
Repeat the overlap check with the next relevant pair of time periods.
Keep going until you've checked all time periods in both lists. You will have a list of all the overlaps.

Code Implementation

def interval_intersection(first_list, second_list):
    intersection_list = []
    first_list_index = 0
    second_list_index = 0

    while first_list_index < len(first_list) and second_list_index < len(second_list):
        first_interval_start, first_interval_end = first_list[first_list_index]
        second_interval_start, second_interval_end = second_list[second_list_index]

        # Check if the intervals overlap.
        if first_interval_end >= second_interval_start and second_interval_end >= first_interval_start:
            # Determine the start and end of the intersection.
            intersection_start = max(first_interval_start, second_interval_start)
            intersection_end = min(first_interval_end, second_interval_end)
            intersection_list.append([intersection_start, intersection_end])

        # Advance the pointer of the interval that ends sooner.
        if first_interval_end < second_interval_end:
            first_list_index += 1

            # The current interval from the first list is fully processed. 

        else:
            second_list_index += 1

            # The current interval from the second list is fully processed.

    return intersection_list

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(m + n) – The algorithm iterates through two lists of intervals, 'firstList' of size 'm' and 'secondList' of size 'n', using two pointers. Each pointer advances based on which interval ends sooner. In each step, a constant amount of work is performed (overlap check and pointer increment). Since each pointer advances at most to the end of its respective list, the algorithm performs at most m + n steps, making the time complexity O(m + n).

Space Complexity

O(min(N, M)) – The algorithm's space complexity is determined by the size of the list used to store the intersecting intervals. In the worst case, every interval in the shorter list might intersect with an interval in the longer list. If N is the number of intervals in the first list and M is the number of intervals in the second list, the maximum size of the result list is limited by the number of intervals in the shorter list, leading to a space complexity of O(min(N, M)). We are not using any additional data structures other than the result list.

Edge Cases

Case	How to Handle
Both input lists are empty	Return an empty list since there are no intervals to intersect.
One input list is empty, the other is not	Return an empty list since no intersection is possible with an empty list.
Intervals in firstList and secondList are disjoint (no intersection)	The algorithm should correctly identify the lack of overlap and return an empty list.
Intervals in firstList are entirely contained within intervals of secondList (or vice versa)	The algorithm correctly finds the intersecting intervals, which would be the intervals of the smaller list in this scenario.
Intervals have the same start or end point (touching)	The condition a[1] >= b[0] && b[1] >= a[0] must include equality to account for touching intervals and find the intersection, which could be a single point.
Large number of intervals in both lists	The two-pointer approach ensures the algorithm has a time complexity of O(m+n), which scales linearly with the input sizes.
Integer overflow if start/end points are very large	Use long data types or check for potential overflow before performing calculations to prevent incorrect results.
Intervals with negative start/end values	The provided comparisons should correctly handle negative values for interval start and end points.