Invert Binary Tree
EasyGiven the root of a binary tree, invert the tree, and return its root.
Example 1:
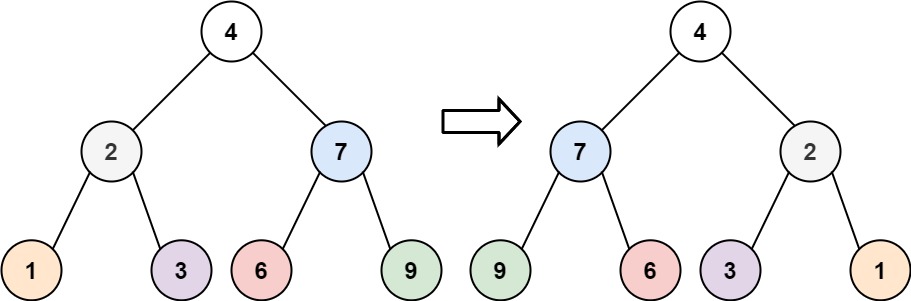
Input: root = [4,2,7,1,3,6,9] Output: [4,7,2,9,6,3,1]
Example 2:
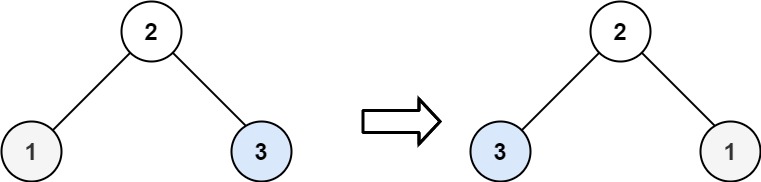
Input: root = [2,1,3] Output: [2,3,1]
Example 3:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 100]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that a node can have in the binary tree?
- Can the tree be empty (i.e., root is null)? If so, what should I return?
- Is it a valid binary tree? (e.g. No cycles, following binary tree structure)
- Do I need to create a new tree, or can I modify the existing tree in place?
- Should I handle the case where any subtree is null?
Brute Force Solution
Approach
Inverting a binary tree means swapping the left and right children of every node in the tree. The brute force approach involves looking at each node individually and performing the swap.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root node.
- For that node, switch its left child with its right child.
- Now, go down to the left child of the original root (which is now on the right side after the swap). Switch its left and right children.
- Next, go to the right child of the original root (which is now on the left side after the swap). Switch its left and right children.
- Continue this process, moving down level by level, swapping the left and right children of each node you encounter.
- Repeat until you've visited every single node in the tree and performed the swap.
- The final tree is the inverted version.
Code Implementation
def invert_binary_tree_brute_force(root):
if root is None:
return None
# Swap the left and right children of the current node.
root.left, root.right = root.right, root.left
# Recursively invert the left subtree.
invert_binary_tree_brute_force(root.left)
# Recursively invert the right subtree.
invert_binary_tree_brute_force(root.right)
return rootBig(O) Analysis
Optimal Solution
Approach
To invert a binary tree, we aim to swap the left and right children of each node throughout the tree. We process the tree in a way that ensures we visit every part of the tree to perform this swap systematically. This approach avoids redundant operations and makes sure we touch every connection once.
Here's how the algorithm would work step-by-step:
- Start by looking at the very top node of the tree.
- Exchange the positions of its left and right child. What was on the left is now on the right, and vice-versa.
- Move down to the left child of the top node, and do the same thing: swap its left and right children.
- Then, move down to the right child of the top node, and also swap its left and right children.
- Continue this process, going deeper and deeper into the tree, swapping children at each node you encounter.
- Keep going until you've reached the very bottom of the tree and swapped the children of every single node.
- By doing this systematically, from top to bottom, you effectively flip the entire tree, mirroring it across its center.
Code Implementation
def invert_binary_tree(root):
if root:
# Swap the left and right children of the current node.
root.left, root.right = root.right, root.left
# Recursively invert the left subtree.
invert_binary_tree(root.left)
# Recursively invert the right subtree.
invert_binary_tree(root.right)
return rootBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return null immediately as there's nothing to invert. |
| Tree with only a root node (no left or right children) | Return the root node itself as it's already 'inverted'. |
| Skewed tree (e.g., all nodes only have left children) | The recursive calls will still proceed down the skewed branch, correctly inverting the tree structure. |
| Tree with duplicate values | Duplicate values do not affect the inversion logic; the structure is the only thing being modified. |
| Very large tree (potential stack overflow with recursion) | While recursion is the natural approach, consider iterative solution using a stack to avoid exceeding stack limits. |
| Tree with negative values | Negative values do not affect the inversion logic; node structure is being modified, not node values. |
| Perfectly balanced tree | The inversion logic applies correctly and efficiently to a perfectly balanced tree. |
| Integer overflow in node values (if applicable in other tree problems but good to check) | The values themselves are not modified during the inversion, so integer overflow is irrelevant in this specific problem. |