Island Perimeter
EasyYou are given row x col grid representing a map where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes", meaning the water inside isn't connected to the water around the island. One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
Example 1:
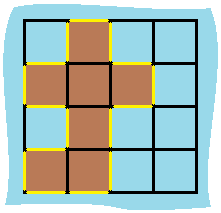
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] Output: 16 Explanation: The perimeter is the 16 yellow stripes in the image above.
Example 2:
Input: grid = [[1]] Output: 4
Example 3:
Input: grid = [[1,0]] Output: 4
Constraints:
row == grid.lengthcol == grid[i].length1 <= row, col <= 100grid[i][j]is0or1.- There is exactly one island in
grid.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (maximum rows and columns)?
- Is the grid guaranteed to contain only one island, or could there be zero islands?
- What is the data type of the grid elements (e.g., integer)? Are values other than 0 and 1 possible?
- Is the input grid guaranteed to be surrounded by water (all edge cells are 0), or do I need to handle cases where the island touches the boundary?
- If the grid is empty, what should the perimeter be (e.g., 0)?
- Are the dimensions of the grid bounded by a maximum value?
Brute Force Solution
Approach
The brute force approach to finding the island perimeter is like meticulously checking every single piece of land. We'll look at each square of land and see if it has any edges that are exposed to water. The total number of these exposed edges will be our perimeter.
Here's how the algorithm would work step-by-step:
- Go through each square in the grid one by one.
- If a square is land, look at its four sides (up, down, left, and right).
- For each side of the land square, check if it's next to water or if it's at the edge of the grid (meaning it's exposed to the outside).
- If a side is next to water or is an edge, then that side contributes to the island's perimeter. Count it.
- After checking all the land squares and their sides, add up all the counted sides. This sum is the total perimeter of the island.
Code Implementation
def island_perimeter(grid):
total_perimeter = 0
number_rows = len(grid)
number_columns = len(grid[0])
for row_index in range(number_rows):
for column_index in range(number_columns):
if grid[row_index][column_index] == 1:
# Check each side of the land cell
if row_index == 0 or grid[row_index - 1][column_index] == 0:
# Top edge contributes to perimeter
total_perimeter += 1
if row_index == number_rows - 1 or grid[row_index + 1][column_index] == 0:
# Bottom edge contributes to perimeter
total_perimeter += 1
if column_index == 0 or grid[row_index][column_index - 1] == 0:
# Left edge contributes to perimeter
total_perimeter += 1
if column_index == number_columns - 1 or grid[row_index][column_index + 1] == 0:
# Right edge contributes to perimeter
total_perimeter += 1
return total_perimeterBig(O) Analysis
Optimal Solution
Approach
The most efficient way to find the island's perimeter is to focus on the transitions between land and water. Instead of checking every cell, we count only the sides of land cells that are exposed to water (or the edge of the grid). This avoids redundant calculations.
Here's how the algorithm would work step-by-step:
- Go through each square of the map, one by one.
- If the current square is land, check each of its four sides.
- For each side, see if it's next to water, or if it's on the edge of the map.
- If a side is next to water or on the edge, count that side as part of the island's perimeter.
- Add up all the counted sides to get the total perimeter.
Code Implementation
def islandPerimeter(grid):
number_of_rows = len(grid)
number_of_columns = len(grid[0])
perimeter = 0
for row in range(number_of_rows):
for column in range(number_of_columns):
if grid[row][column] == 1:
# Check each land cell.
if row == 0:
perimeter += 1
elif grid[row - 1][column] == 0:
perimeter += 1
if row == number_of_rows - 1:
perimeter += 1
elif grid[row + 1][column] == 0:
perimeter += 1
if column == 0:
perimeter += 1
elif grid[row][column - 1] == 0:
perimeter += 1
if column == number_of_columns - 1:
perimeter += 1
elif grid[row][column + 1] == 0:
perimeter += 1
return perimeter
def island_perimeter(grid):
rows = len(grid)
columns = len(grid[0])
island_perimeter_size = 0
for row_index in range(rows):
for column_index in range(columns):
if grid[row_index][column_index] == 1:
#Top edge or water above
if row_index == 0 or grid[row_index - 1][column_index] == 0:
island_perimeter_size += 1
#Bottom edge or water below
if row_index == rows - 1 or grid[row_index + 1][column_index] == 0:
island_perimeter_size += 1
#Left edge or water to the left
if column_index == 0 or grid[row_index][column_index - 1] == 0:
island_perimeter_size += 1
#Right edge or water to the right
if column_index == columns - 1 or grid[row_index][column_index + 1] == 0:
island_perimeter_size += 1
return island_perimeter_sizeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 perimeter, as there is no island. |
| Grid with zero rows or zero columns | Return 0 perimeter, since there is no island. |
| Grid with a single cell that is land (1) | Return 4, as the single land cell has 4 sides exposed to water. |
| Grid filled entirely with water (all 0s) | Return 0, since there is no land. |
| Grid filled entirely with land (all 1s) | Calculate perimeter based on grid dimensions: 2*(rows + cols). |
| Large grid (potentially exceeding memory limits if not handled efficiently) | Iterate through the grid row by row and cell by cell, calculating the perimeter on the fly to avoid storing large intermediate results. |
| Integer overflow in perimeter calculation (unlikely but possible with very large grids) | Use a 64-bit integer to store the perimeter, or check for overflow during calculations if 64-bit integers are unavailable. |
| Invalid input (values other than 0 or 1 in the grid) | Assume the input is valid as stated in problem description, otherwise add a check to treat values other than 0 or 1 as water, or raise an exception. |