K Highest Ranked Items Within a Price Range #4 Most Asked
MediumYou are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:
0represents a wall that you cannot pass through.1represents an empty cell that you can freely move to and from.- All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.
It takes 1 step to travel between adjacent grid cells.
You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.
You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:
- Distance, defined as the length of the shortest path from the
start(shorter distance has a higher rank). - Price (lower price has a higher rank, but it must be in the price range).
- The row number (smaller row number has a higher rank).
- The column number (smaller column number has a higher rank).
Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.
Example 1:
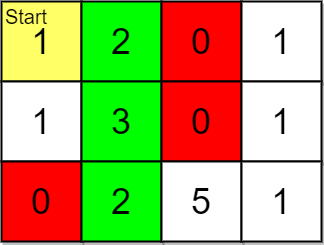
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3 Output: [[0,1],[1,1],[2,1]] Explanation: You start at (0,0). With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2). The ranks of these items are: - (0,1) with distance 1 - (1,1) with distance 2 - (2,1) with distance 3 - (2,2) with distance 4 Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).
Example 2:
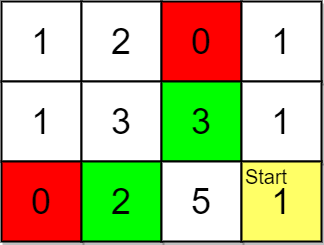
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2 Output: [[2,1],[1,2]] Explanation: You start at (2,3). With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1). The ranks of these items are: - (2,1) with distance 2, price 2 - (1,2) with distance 2, price 3 - (1,1) with distance 3 - (0,1) with distance 4 Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).
Example 3:
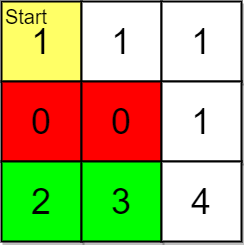
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3 Output: [[2,1],[2,0]] Explanation: You start at (0,0). With a price range of [2,3], we can take items from (2,0) and (2,1). The ranks of these items are: - (2,1) with distance 5 - (2,0) with distance 6 Thus, the 2 highest ranked items in the price range are (2,1) and (2,0). Note that k = 3 but there are only 2 reachable items within the price range.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1051 <= m * n <= 1050 <= grid[i][j] <= 105pricing.length == 22 <= low <= high <= 105start.length == 20 <= row <= m - 10 <= col <= n - 1grid[row][col] > 01 <= k <= m * n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (maximum rows and columns), and what is the maximum value for prices within the grid and in the `pricing` array?
- If no items are within the price range, or if the grid is empty, what should the function return?
- If multiple items have the same distance, price, row, and column, should duplicates be included in the result, or should the first k unique items be returned?
- Are the start coordinates guaranteed to be valid and within the bounds of the grid, and will the start cell always be walkable (value greater than or equal to 1)?
- When sorting by rank, what is the tie-breaking order if multiple items have the same distance and price? Is it row index first, then column index, or the reverse?
Brute Force Solution
Approach
The brute force approach to finding the best items involves checking every single item in the store. We look at each item's price and location, and compare it to the other items to find the highest ranked ones within the given price range.
Here's how the algorithm would work step-by-step:
- Go through each item in the store, one by one.
- For each item, check if its price falls within the allowed price range.
- If the price is okay, calculate its distance from our starting point.
- Store this item along with its price, distance, and rank (which is just the item's value).
- After checking every item in the store, we now have a list of all the valid items (those within the price range).
- Sort the valid items based on rank, distance, and then price (if ranks and distances are the same). Higher rank is better and shorter distance is better, and lower price is better.
- Finally, pick the top K items from the sorted list.
Code Implementation
def k_highest_ranked_items(
grid, pricing, start, k_items
):
row_count = len(grid)
column_count = len(grid[0])
min_price = pricing[0]
max_price = pricing[1]
start_row = start[0]
start_column = start[1]
valid_items = []
for row in range(row_count):
for column in range(column_count):
item_price = grid[row][column]
# Check the price falls within the allowed range
if min_price <= item_price <= max_price and item_price != 0:
distance = abs(row - start_row) + abs(column - start_column)
rank = grid[row][column]
valid_items.append(
(distance, rank, item_price, row, column)
)
# Sort by distance, rank, then price.
valid_items.sort(key=lambda x: (x[0], -x[1], x[2]))
# Extract the coordinates of the top k items
result = []
# Build final result
for i in range(min(k_items, len(valid_items))):
result.append([valid_items[i][3], valid_items[i][4]])
return resultBig(O) Analysis
Optimal Solution
Approach
The best way to find the highest-ranked items within a price range is to explore the area around the starting point in ever-expanding circles, checking items as you go. This prevents checking every single location. Prioritize closer, relevant items to ensure the top K items are discovered quickly and efficiently.
Here's how the algorithm would work step-by-step:
- Start at the customer's location on the map.
- Explore the map in layers, like ripples expanding outwards from a pebble dropped in water. Check locations that are 1 step away, then 2 steps away, then 3 steps away, and so on.
- As you explore each location, check if the item there is within the allowed price range.
- If an item is in the correct price range, calculate its rank based on its distance from the customer and its inherent ranking (higher is better).
- Keep track of the best K items found so far, always ensuring you only store the best ones based on their rank.
- Continue expanding outwards until you have found K items, or you have exhausted the entire map. If you exhaust the map before finding K items, return the items you have found.
- When prioritizing which directions to explore, consider prioritizing locations closer to the starting point. This will naturally lead to exploring closer items first, which are more likely to be higher ranked.
Code Implementation
def k_highest_ranked_items(
grid, pricing, start, k_items
):
rows = len(grid)
cols = len(grid[0])
minimum_price = pricing[0]
maximum_price = pricing[1]
start_row = start[0]
start_col = start[1]
queue = [(0, start_row, start_col)]
visited = set()
visited.add((start_row, start_col))
items = []
while queue:
distance, current_row, current_col = queue.pop(0)
price = grid[current_row][current_col]
# Check if the current item is within the price range
if (
minimum_price <= price <= maximum_price
and price != 0
):
items.append(
(distance, price, current_row, current_col)
)
# Explore adjacent cells
directions = [
(0, 1),
(0, -1),
(1, 0),
(-1, 0),
]
for direction_row, direction_col in directions:
next_row = current_row + direction_row
next_col = current_col + direction_col
# Ensure the neighboring cell is valid and not visited
if (
0 <= next_row < rows
and 0 <= next_col < cols
and (next_row, next_col) not in visited
and grid[next_row][next_col] != 0
):
queue.append(
(distance + 1, next_row, next_col)
)
visited.add((next_row, next_col))
# Sort items by distance, price, then row and column
items.sort(
key=lambda item: (
item[0],
-item[1],
item[2],
item[3],
)
)
# Return the top k items
result = [
[item[2], item[3]] for item in items[:k_items]
]
return resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return an empty list if the grid is null or empty as there are no items to search. |
| Invalid start position (out of bounds) | Return an empty list if the start position is out of bounds of the grid. |
| Pricing range where low price is greater than high price | Treat this as an empty range and return appropriate number of elements. |
| k is zero or negative | Return an empty list if k is zero or negative because no items are requested. |
| Grid contains only blocked cells (all zeros) | Return an empty list as there are no items to consider. |
| No items within the specified price range | Return an empty list since there are no items that match the criteria. |
| k is larger than the number of items within the price range | Return all the items within the price range, sorted as specified. |
| Integer overflow when calculating distance (especially on large grids) | Use appropriate data types (e.g., long) for distance calculation or limit grid size. |