K Radius Subarray Averages

Medium

Asked by:

22 views

Topics:

ArraysSliding Windows

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

Example 1:

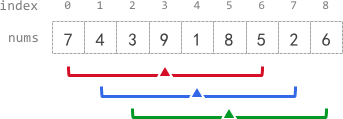
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

Constraints:

n == nums.length
1 <= n <= 10⁵
0 <= nums[i], k <= 10⁵

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the size of the input array `nums` and the value of `k`? Are they large enough to warrant concerns about integer overflow during the summation?
Can the elements in the input array `nums` be negative, zero, or floating-point numbers, or are they guaranteed to be non-negative integers?
If `k` is larger than or equal to half the length of `nums`, such that no averages can be computed, what should the function return? Should I return an array filled with -1's, or an empty array?
For a given index `i`, if `i - k` or `i + k` are out of bounds, should the corresponding element in the result array be -1?
If the average is not an integer, should I truncate it (round down), round up, or round to the nearest integer?

Brute Force Solution

Approach

To find the average of subarrays within a certain range, the brute force method looks at every possible subarray. For each of those subarrays, it calculates the average by summing the numbers within it, and then divides that sum by the number of elements. Finally the averages are stored, one for each possible subarray that fit the requirements.

Here's how the algorithm would work step-by-step:

Start by picking a position in the sequence.
Check if there are enough numbers to the left and right of this position, according to our specified range.
If there aren't enough, mark this position as having no average.
If there are enough, add up all the numbers within the range around that position, including the number at that position itself.
Divide the sum you just calculated by the total number of numbers you added together.
Record this result as the average for that position.
Move to the next position in the sequence and repeat steps 2 through 6.
Once you have gone through every position, you will have the averages for all positions that have enough neighbors within the range.

Code Implementation

def k_radius_subarray_averages_brute_force(numbers, radius):
    array_length = len(numbers)
    averages = [-1] * array_length

    for center_index in range(array_length):
        # Check if enough elements exist to form subarray
        if center_index - radius >= 0 and center_index + radius < array_length:
            
            subarray_sum = 0
            subarray_length = 2 * radius + 1

            # Sum all elements within the radius
            for index in range(center_index - radius, center_index + radius + 1):
                subarray_sum += numbers[index]

            averages[center_index] = int(subarray_sum / subarray_length)

    return averages

Big(O) Analysis

Time Complexity

O(n*k) – The algorithm iterates through the input array nums of size n. For each element at index i, it checks if there are k elements to its left and k elements to its right. If the condition is met, a sum of the 2k+1 elements centered at index i is computed. This summation involves iterating through a subarray of size 2k+1 which is O(k). Since this process is repeated for each of the n elements, the overall time complexity becomes O(n*k), where k is the radius.

Space Complexity

O(1) – The algorithm outlined in the plain English explanation primarily focuses on in-place calculations and storing the final averages. It iterates through each position in the sequence and calculates the average for a subarray around that position. The averages are stored in an array of size N, which is ultimately returned and thus counts toward the problem's output and not auxiliary space. The only additional space used is for variables to store the sum and the count during the average calculation, and the loop counter which are constant regardless of the input size N. Therefore, the auxiliary space complexity is O(1).

Optimal Solution

Approach

The key idea is to avoid recalculating the sum of each subarray. We can efficiently compute the average by reusing the sum from the previous subarray. We'll maintain a sliding window of sums and update it as we move through the input.

Here's how the algorithm would work step-by-step:

First, think about how many positions in the input are even possible centers for the averaging calculation. If the input isn't long enough to have the needed number of elements on both sides (specified by the radius `k`), then those positions can't have averages.
Next, create a running sum as you move across the input. This running sum will keep track of the sum of the numbers within the window that will be used to calculate each average. Keep adding numbers to the running sum until you have a window of the correct size.
When you reach a point where you have the correct number of elements within the window, you can compute the average. Add this average to a place where the results will be stored.
After calculating the average for that central element, slide the window by removing the element on the left edge of the window from the running sum and adding the next element on the right side of the input to the running sum.
Continue sliding the window and calculating averages until you reach the end of the input.
Finally, return the list of calculated averages. If a position could not be a center, it should be marked with a specific value (like -1).

Code Implementation

def k_radius_subarray_averages(numbers, radius):
    number_of_elements = len(numbers)
    result = [-1] * number_of_elements
    
    # Not enough elements to form any averages
    if number_of_elements < 2 * radius + 1:
        return result

    window_sum = 0
    # Calculate the sum of the first window
    for i in range(2 * radius + 1):
        window_sum += numbers[i]

    result[radius] = window_sum // (2 * radius + 1)

    # Slide the window and calculate averages
    for center_index in range(radius + 1, number_of_elements - radius):
        window_sum -= numbers[center_index - radius - 1]
        window_sum += numbers[center_index + radius]
        result[center_index] = window_sum // (2 * radius + 1)
        
    return result

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through the input array of size n once to calculate the running sum and the averages. The sliding window operations (adding and subtracting elements from the running sum) take constant time. Therefore, the time complexity is directly proportional to the input size n, resulting in O(n).

Space Complexity

O(N) – The algorithm creates a list of calculated averages to store the results. The size of this list is directly proportional to the input size N, where N is the length of the input array. Each position in the list will store the calculated average or -1. Therefore, the auxiliary space required is O(N).

Edge Cases

Case	How to Handle
Null or empty input array nums	Return an empty array if nums is null or empty, as no averages can be calculated.
k is zero	Each element's average is just the element itself; return the original array.
k is greater than or equal to half the length of nums (k >= nums.length // 2)	The first and last k indices will not have k elements on both sides, so handle the beginning and ending indices accordingly based on the problem description's edge case handling guidelines.
nums array contains negative numbers	The sliding window approach will correctly calculate the average, including negative numbers.
nums array contains large positive numbers that could cause integer overflow during summation	Use long data type to store sums to prevent integer overflow.
nums array contains zero values	The sliding window approach will correctly calculate the average, including zero values.
nums array with very large length and large k, triggering time limit exceeded	Optimize sliding window by subtracting the leftmost element and adding the rightmost element, avoiding recalculating the sum each time.
All elements in nums are the same value	The sliding window approach will correctly calculate the average which will be the value of element.

Null or empty input array nums

How to Handle:

Return an empty array if nums is null or empty, as no averages can be calculated.

k is zero

How to Handle:

Each element's average is just the element itself; return the original array.

k is greater than or equal to half the length of nums (k >= nums.length // 2)

How to Handle:

The first and last k indices will not have k elements on both sides, so handle the beginning and ending indices accordingly based on the problem description's edge case handling guidelines.

nums array contains negative numbers

How to Handle:

The sliding window approach will correctly calculate the average, including negative numbers.

nums array contains large positive numbers that could cause integer overflow during summation

How to Handle:

Use long data type to store sums to prevent integer overflow.

nums array contains zero values

How to Handle:

The sliding window approach will correctly calculate the average, including zero values.

nums array with very large length and large k, triggering time limit exceeded

How to Handle:

Optimize sliding window by subtracting the leftmost element and adding the rightmost element, avoiding recalculating the sum each time.

All elements in nums are the same value

How to Handle:

The sliding window approach will correctly calculate the average which will be the value of element.