Knight Dialer

Medium

Asked by:

45 views

Topics:

Dynamic Programming

The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagram:

A chess knight can move as indicated in the chess diagram below:

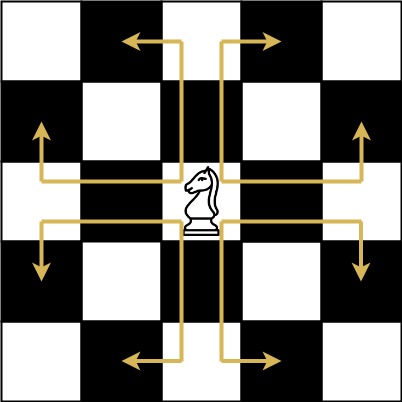
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).

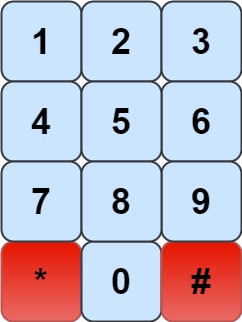
Given an integer n, return how many distinct phone numbers of length n we can dial.

You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.

As the answer may be very large, return the answer modulo 10⁹ + 7.

Example 1:

Input: n = 1
Output: 10
Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.

Example 2:

Input: n = 2
Output: 20
Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

Example 3:

Input: n = 3131
Output: 136006598
Explanation: Please take care of the mod.

Constraints:

1 <= n <= 5000

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the maximum number of hops (N) the knight can make?
Are we concerned about integer overflow given the number of paths could grow exponentially?
Is the starting position fixed, or can the knight start on any of the dial positions?
Should the returned count be modulo some number?
What number does each key on the phone dial pad represent (specifically what number, if any, does '*' and '#' represent)?

Brute Force Solution

Approach

The Knight Dialer problem asks us to find how many phone numbers of a certain length can be dialed by a knight on a phone keypad. A brute force approach would try every possible sequence of knight moves to create these phone numbers. It essentially explores all paths the knight can take.

Here's how the algorithm would work step-by-step:

Start at one of the numbers on the keypad.
From that starting number, check every possible number the knight can jump to.
For each of those possible jumps, again check every possible number the knight can jump to next.
Keep repeating this process for the required number of jumps (the phone number length).
Each time you reach the desired phone number length, count that sequence as a valid phone number.
Do this starting from every number on the keypad.
The final answer is the total count of all valid phone numbers found from all starting numbers.

Code Implementation

def knight_dialer_brute_force(phone_number_length):
    keypad = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9],
        ['*', 0, '#']
    ]
    
    knight_moves = {
        0: [4, 6],
        1: [6, 8],
        2: [7, 9],
        3: [4, 8],
        4: [0, 3, 9],
        5: [],
        6: [0, 1, 7],
        7: [2, 6],
        8: [1, 3],
        9: [2, 4]
    }
    
    valid_phone_numbers_count = 0
    
    def is_valid_move(row, column):
        return 0 <= row < 4 and 0 <= column < 3 and keypad[row][column] != '*' and keypad[row][column] != '#'

    def dial_number(current_number, remaining_length):
        nonlocal valid_phone_numbers_count
        
        if remaining_length == 1:
            valid_phone_numbers_count += 1
            return

        # Get valid knight moves from current digit.
        possible_moves = knight_moves[current_number]

        for next_number in possible_moves:
            dial_number(next_number, remaining_length - 1)

    # Iterate to start number on each digit.
    for start_row in range(4):
        for start_column in range(3):
            start_digit = keypad[start_row][start_column]
            if start_digit != '*' and start_digit != '#':
                dial_number(start_digit, phone_number_length)

    # Because 5 is not considered valid.
    return valid_phone_numbers_count

Big(O) Analysis

Time Complexity

O(10 * 8^n) – The provided brute force approach explores all possible knight moves recursively. Starting from each of the 10 digits, the algorithm branches out, checking all possible next digits a knight can jump to. In the worst case, from each digit, the knight has up to 8 possible moves (though in reality some digits have fewer). This branching occurs for each digit in the phone number, which has length n. Therefore, the algorithm explores roughly 10 (starting positions) * 8^n (possible paths) possibilities. This exponential growth makes the time complexity O(10 * 8^n).

Space Complexity

O(N) – The brute force approach explores all possible paths the knight can take using recursion. Each recursive call adds a new frame to the call stack. The depth of the recursion corresponds to the phone number length, denoted as N. Thus, the maximum height of the recursion tree (and therefore the maximum number of stack frames) is N, leading to a space complexity of O(N) due to the recursion stack.

Optimal Solution

Approach

The most efficient way to solve this problem is to realize that the number of ways to dial a number of a specific length only depends on how many ways you could dial numbers of the previous length. We can leverage this fact to avoid recalculating the same information repeatedly. This is done through a technique called dynamic programming.

Here's how the algorithm would work step-by-step:

Imagine each number on the phone as a possible starting point.
Think about how many ways you can dial a 1-digit number starting from each number. It's just one way from each, since you start and end on that number.
Now, consider how many ways you can dial a 2-digit number. From each starting number, a knight can only jump to certain other numbers. Count how many valid 2-digit numbers you can make from each starting number.
Next, for a 3-digit number, use the counts you found for 2-digit numbers. For each starting number, find the numbers a knight can jump to, and add the number of ways to make a 2-digit number starting from each of those jumped-to numbers.
Repeat this process for longer numbers, always using the counts from the previous length to calculate the counts for the current length.
By doing this, you avoid recalculating the same paths over and over. Each time you compute the number of ways to dial a number of a certain length, you're building on the work you've already done.
After finding the number of ways for each starting digit for the required length of dialed numbers, simply add up the ways from each number to get the grand total. Make sure the grand total does not overflow, taking the modulo as needed.

Code Implementation

def knight_dialer(dial_length):
    modulo = 10**9 + 7
    knight_moves = {
        1: [6, 8],
        2: [7, 9],
        3: [4, 8],
        4: [0, 3, 9],
        5: [],
        6: [0, 1, 7],
        7: [2, 6],
        8: [1, 3],
        9: [2, 4],
        0: [4, 6]
    }

    # Initialize ways to dial a 1-digit number from each starting number.
    number_of_ways = [1] * 10

    # Iterate to calculate ways for longer numbers.
    for _ in range(1, dial_length):
        next_number_of_ways = [0] * 10
        for start_digit in range(10):
            # For each digit, find possible knight moves.
            for next_digit in knight_moves[start_digit]:

                # Accumulate ways from the previous length.
                next_number_of_ways[next_digit] = (next_number_of_ways[next_digit] + number_of_ways[start_digit]) % modulo

        number_of_ways = next_number_of_ways

    # Sum up the ways from each starting digit for the final result.
    total_ways = 0
    for ways in number_of_ways:
        total_ways = (total_ways + ways) % modulo

    return total_ways

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates n times, where n is the desired length of the dialed number. In each iteration, it updates the count of possible numbers from each digit based on the counts from the previous iteration. Since there is a fixed number of digits (10 on a standard phone dialpad) and a fixed number of possible knight moves from each digit, the inner operation within each iteration takes constant time, regardless of n. Therefore, the runtime is dominated by the single loop that runs n times, giving a time complexity of O(n).

Space Complexity

O(1) – The described dynamic programming approach uses an array (or similar data structure) to store the number of ways to dial numbers of a certain length for each starting digit. Since we only need to keep track of the results from the previous length to calculate the current length, we only need to store two such arrays, one for the previous length and one for the current length. The size of each of these arrays is fixed (10, corresponding to the digits 0-9), irrespective of the input N (the length of the dialed number). Therefore, the auxiliary space used is constant.

Edge Cases

Case	How to Handle
Input n is zero	Return 0, as there are no possible sequences of length zero.
Input n is one	Return 10, as any of the 10 digits can be the starting digit.
Large n leading to integer overflow	Use modular arithmetic to prevent the count from exceeding the maximum integer value, and return modulo 10^9 + 7.
Negative input for n	Return 0 as a negative sequence length is nonsensical.
n close to the maximum integer value	Ensure the DP array or recursion doesn't exceed stack or memory limits, and optimize for space efficiency.
All starting numbers lead to zero valid sequences after a few hops	The algorithm will naturally return 0 after exploring all possible paths.
Symmetric phone keypad structure and its impact on optimization	Recognize that some starting digits will have the same counts, and optimize DP by only computing for unique starting positions.
Cycles in keypad traversal affect correctness	The DP table prevents infinite recursion by storing previously computed results, avoiding cycle issues automatically.

Input n is zero

How to Handle:

Return 0, as there are no possible sequences of length zero.

Input n is one

How to Handle:

Return 10, as any of the 10 digits can be the starting digit.

Large n leading to integer overflow

How to Handle:

Use modular arithmetic to prevent the count from exceeding the maximum integer value, and return modulo 10^9 + 7.

Negative input for n

How to Handle:

Return 0 as a negative sequence length is nonsensical.

n close to the maximum integer value

How to Handle:

Ensure the DP array or recursion doesn't exceed stack or memory limits, and optimize for space efficiency.

All starting numbers lead to zero valid sequences after a few hops

How to Handle:

The algorithm will naturally return 0 after exploring all possible paths.

Symmetric phone keypad structure and its impact on optimization

How to Handle:

Recognize that some starting digits will have the same counts, and optimize DP by only computing for unique starting positions.

Cycles in keypad traversal affect correctness

How to Handle:

The DP table prevents infinite recursion by storing previously computed results, avoiding cycle issues automatically.