Largest Local Values in a Matrix
EasyYou are given an n x n integer matrix grid.
Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:
maxLocal[i][j]is equal to the largest value of the3 x 3matrix ingridcentered around rowi + 1and columnj + 1.
In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.
Return the generated matrix.
Example 1:
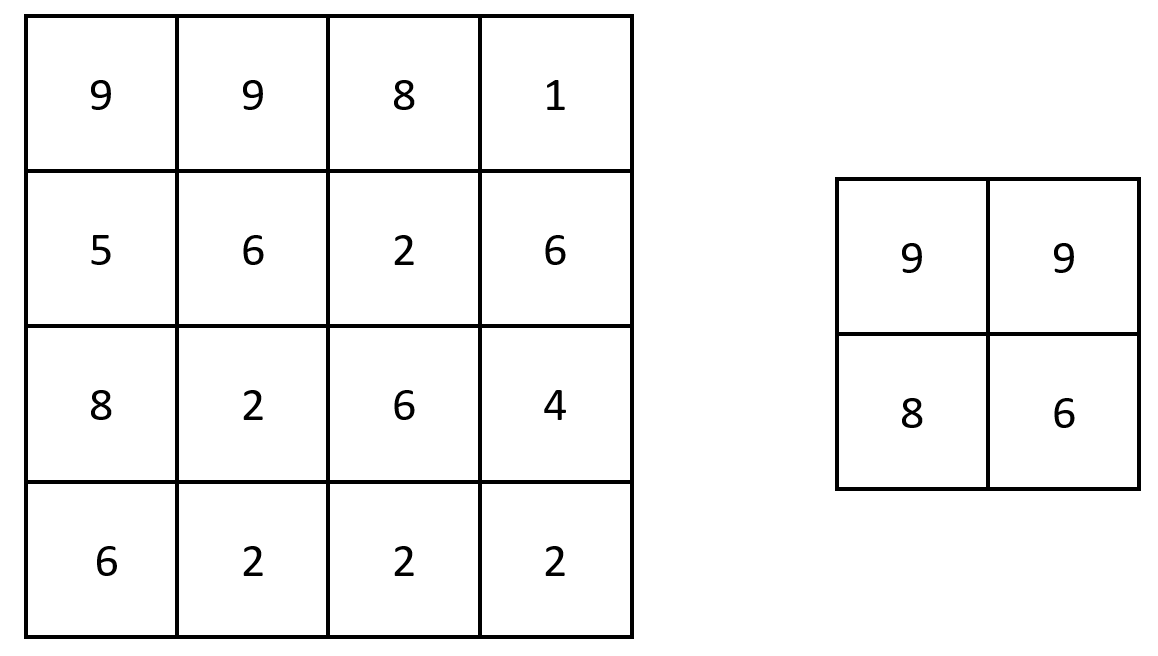
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]] Output: [[9,9],[8,6]] Explanation: The diagram above shows the original matrix and the generated matrix. Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.
Example 2:
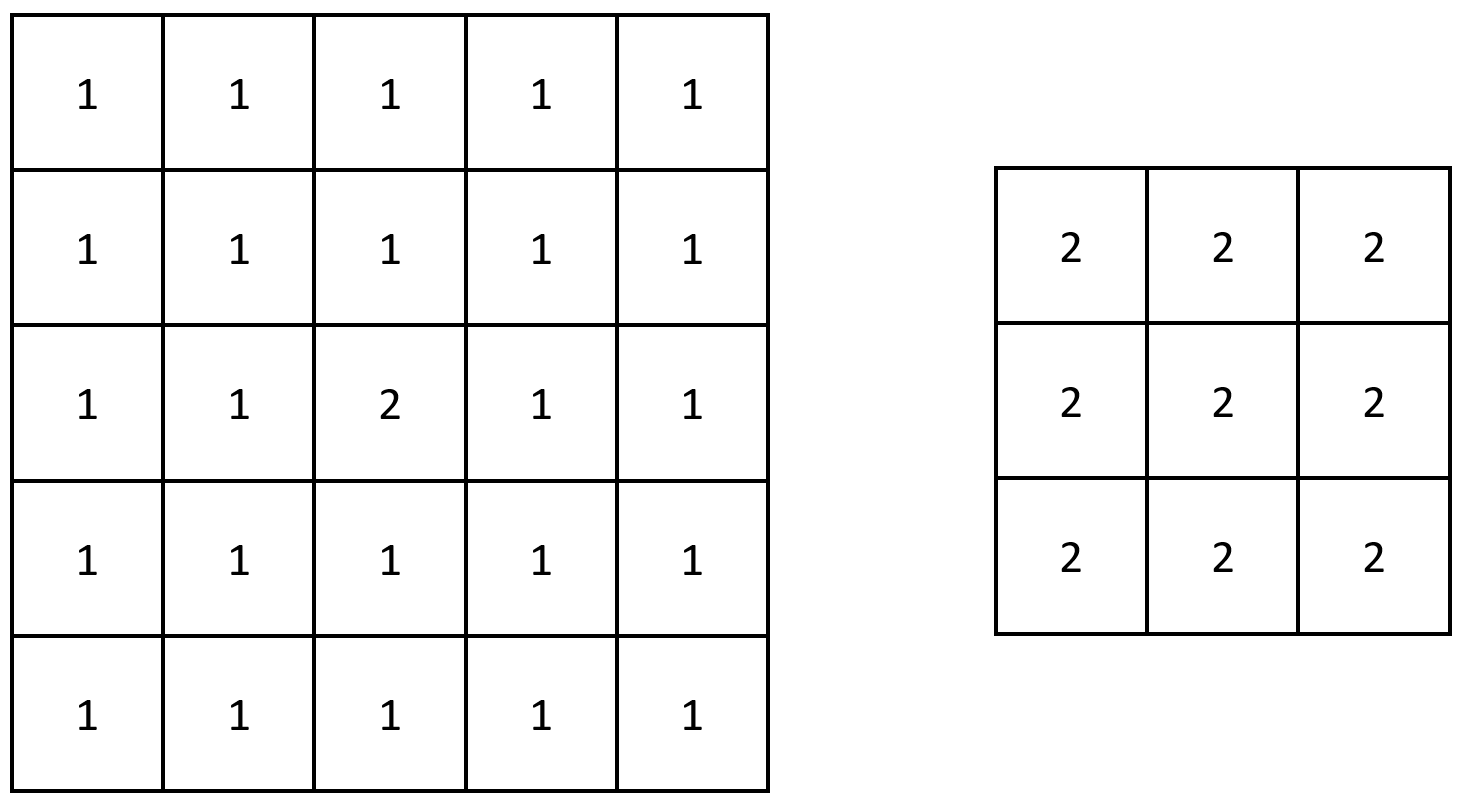
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]] Output: [[2,2,2],[2,2,2],[2,2,2]] Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.
Constraints:
n == grid.length == grid[i].length3 <= n <= 1001 <= grid[i][j] <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the dimensions of the matrix (m and n)? What are the upper and lower bounds?
- What is the range of values for the elements within the matrix? Can they be negative, zero, or floating-point numbers?
- If the input matrix has dimensions smaller than 3x3, what should the output be? Should I return an empty matrix or handle it differently?
- Is the input matrix guaranteed to be rectangular (i.e., all rows have the same number of columns)?
- Can you provide an example of the expected output format, especially for the edge cases? I.e., should it be a new matrix with the local maximum or a different format?
Brute Force Solution
Approach
The goal is to find the largest value within each 3x3 square of a bigger grid. The brute force way is to just look at every single possible 3x3 square within the grid and check what the biggest number is.
Here's how the algorithm would work step-by-step:
- Start at the top-left corner of the grid.
- Consider the first 3x3 square in the top-left.
- Look at every number in that 3x3 square and find the largest one.
- Record this largest value as the 'local' largest value for that top-left position.
- Move the 3x3 square one position to the right.
- Repeat the process of finding the largest number within this new 3x3 square and recording it.
- Keep doing this, shifting the 3x3 square to the right, until you reach the edge of the main grid.
- Then, move the 3x3 square down one position and start again from the left edge.
- Continue this process of sliding the 3x3 square across and down until you've covered every possible 3x3 square within the larger grid.
- You will then have a new grid containing the largest value from each of the 3x3 areas of the original grid.
Code Implementation
def largest_local_values_in_matrix(grid):
grid_row_length = len(grid)
grid_column_length = len(grid[0])
# Determine the dimensions of the output matrix
result_row_length = grid_row_length - 2
result_column_length = grid_column_length - 2
result_matrix = [[0] * result_column_length for _ in range(result_row_length)]
# Iterate through each possible 3x3 subgrid
for row_index in range(result_row_length):
for column_index in range(result_column_length):
maximum_value = 0
# Find the maximum value within the current 3x3 subgrid
for i in range(row_index, row_index + 3):
for j in range(column_index, column_index + 3):
maximum_value = max(maximum_value, grid[i][j])
# Store the maximum value in the result matrix
result_matrix[row_index][column_index] = maximum_value
return result_matrixBig(O) Analysis
Optimal Solution
Approach
To find the largest local values efficiently, the best approach is to look at the matrix in a way that avoids repeating calculations. We use a sliding window technique to quickly determine the largest value within each local area.
Here's how the algorithm would work step-by-step:
- First, focus on finding the largest value within each 3x3 area horizontally. For each row, slide a window of size 3 across it, keeping track of the largest value you've seen in that window.
- Next, apply a similar strategy vertically. Take the results from the previous step and slide a window of size 3 down each column, again keeping track of the largest value within the window.
- The largest value found during the vertical sliding window process will be the largest local value for the corresponding 3x3 area in the original matrix.
Code Implementation
def largestLocal(grid):
grid_length = len(grid)
intermediate_matrix = [([0] * (grid_length - 2)) for _ in range(grid_length)]
# Find the maximum value in each 3x3 horizontal window
for row_index in range(grid_length):
for col_index in range(grid_length - 2):
max_horizontal = max(grid[row_index][col_index], grid[row_index][col_index+1], grid[row_index][col_index+2])
intermediate_matrix[row_index][col_index] = max_horizontal
result_matrix = [([0] * (grid_length - 2)) for _ in range(grid_length - 2)]
# Find the maximum value in each 3x3 vertical window using the intermediate result
for row_index in range(grid_length - 2):
for col_index in range(grid_length - 2):
# Need to compare 3 rows to find max value
max_vertical = max(intermediate_matrix[row_index][col_index],
intermediate_matrix[row_index+1][col_index],
intermediate_matrix[row_index+2][col_index])
result_matrix[row_index][col_index] = max_vertical
return result_matrixBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input matrix | Return an empty matrix or throw an exception, depending on problem specifications, to avoid null pointer exceptions. |
| Matrix with dimensions less than 3x3 | Return an empty matrix since a 3x3 local maximum cannot be calculated. |
| Matrix with extremely large dimensions (memory constraints) | Consider using a sliding window approach to minimize memory usage if the entire output cannot fit in memory at once. |
| Matrix with all identical values | The resulting matrix will have the same value everywhere, which the algorithm should handle correctly. |
| Matrix with negative or zero values | The algorithm must correctly handle negative and zero values when finding the maximum within the 3x3 window. |
| Integer overflow when calculating the local maximum | Use a data type large enough to hold the maximum possible value (e.g., long) or check for overflow conditions. |
| Boundary conditions where the 3x3 window extends beyond the matrix boundaries | Ensure that the algorithm only considers elements within the valid bounds of the input matrix when calculating the local maximum for each cell. |
| Large values in the input matrix | Test cases should include large integer numbers to check if there are any integer overflow problems. |