Largest Magic Square
Largest Magic Square #3 Most Asked
MediumA k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.
Given an m x n integer grid, return the size (i.e., the side length k) of the largest magic square that can be found within this grid.
Example 1:
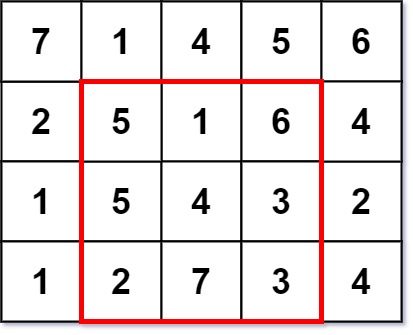
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]] Output: 3 Explanation: The largest magic square has a size of 3. Every row sum, column sum, and diagonal sum of this magic square is equal to 12. - Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12 - Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12 - Diagonal sums: 5+4+3 = 6+4+2 = 12
Example 2:
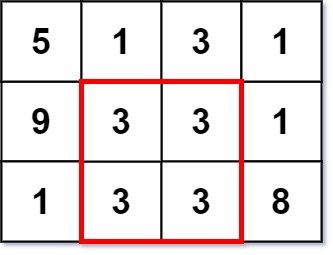
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]] Output: 2
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 106
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the dimensions of the grid (number of rows and columns), and the range of integer values within the grid?
- If no magic square exists within the grid, what value should I return (e.g., 0, -1)?
- Is the input grid guaranteed to be a rectangular matrix (i.e., all rows have the same number of columns)?
- Can I assume the input grid is not null or empty? If it can be, what should I return?
- Is there a lower bound for the size *k* of a magic square that I should look for (e.g., is *k* must be greater than 1)?
Brute Force Solution
Approach
The brute force method to find the biggest magic square involves examining every possible square within the given grid. We test each square to see if it meets the criteria of a magic square, and we keep track of the largest one we find. It's like trying on every possible combination of blocks and seeing which one is the biggest magical block.
Here's how the algorithm would work step-by-step:
- Start by considering the smallest possible square size, which is one element by one element.
- Check if this single element square is a magic square, which it always is.
- Now, increase the size of the square to two elements by two elements.
- Move this 2x2 square around the grid, looking at every possible position.
- For each 2x2 square, calculate the sum of each row, column, and diagonal.
- Check if all these sums are equal. If they are, you've found a magic square!
- Keep track of the size of the biggest magic square you've found so far.
- Increase the square size again to three elements by three elements and repeat the process of moving the square around and checking the sums.
- Keep doing this for all possible square sizes, up to the maximum size that will fit within the original grid.
- After you've tested all possible square sizes and positions, the biggest magic square you kept track of is your answer.
Code Implementation
def largest_magic_square(grid):
rows = len(grid)
cols = len(grid[0]) if rows > 0 else 0
max_square_size = 0
for square_size in range(1, min(rows, cols) + 1):
for row_start in range(rows - square_size + 1):
for col_start in range(cols - square_size + 1):
# Extract the current square subgrid
subgrid = [grid[row_start + i][col_start : col_start + square_size] for i in range(square_size)]
# Check if the current square is a magic square
if is_magic_square(subgrid):
max_square_size = max(max_square_size, square_size)
return max_square_size
def is_magic_square(square):
size = len(square)
if size == 0:
return False
expected_sum = sum(square[0])
# Check if all rows have the same sum
for row in square:
if sum(row) != expected_sum:
return False
# Check if all columns have the same sum
for column_index in range(size):
column_sum = 0
for row_index in range(size):
column_sum += square[row_index][column_index]
if column_sum != expected_sum:
return False
# Check main diagonal sum
main_diagonal_sum = 0
for i in range(size):
main_diagonal_sum += square[i][i]
if main_diagonal_sum != expected_sum:
return False
# Check secondary diagonal sum
secondary_diagonal_sum = 0
for i in range(size):
secondary_diagonal_sum += square[i][size - 1 - i]
# Return false if secondary diagonal doesn't match
if secondary_diagonal_sum != expected_sum:
return False
return True
Big(O) Analysis
Optimal Solution
Approach
To efficiently find the largest magic square within a larger grid, we avoid checking every possible square. The key is to precompute information that allows us to quickly verify if a square is magic, significantly reducing redundant calculations.
Here's how the algorithm would work step-by-step:
- First, create helper tables that store sums of rows, columns, and diagonals of the original grid up to each point.
- Then, start checking for magic squares by looking at the largest possible square size first and working downwards.
- For each potential square size, use the helper tables to quickly calculate the sums of its rows, columns, and diagonals.
- If all row, column, and diagonal sums are equal for a given square, we've found a magic square of that size.
- Since we started with the largest possible size and worked downwards, the first magic square we find will be the largest.
- Stop the process as soon as the first magic square is located to avoid unnecessary computations.
Code Implementation
def largest_magic_square(grid):
rows = len(grid)
cols = len(grid[0])
size = min(rows, cols)
row_sums = [[0] * (cols + 1) for _ in range(rows)]
col_sums = [[0] * (rows + 1) for _ in range(cols)]
for i in range(rows):
for j in range(cols):
row_sums[i][j + 1] = row_sums[i][j] + grid[i][j]
col_sums[j][i + 1] = col_sums[j][i] + grid[i][j]
for square_size in range(size, 0, -1):
for row_start in range(rows - square_size + 1):
for col_start in range(cols - square_size + 1):
magic = True
square_sum = row_sums[row_start][col_start + square_size] - row_sums[row_start][col_start]
# Check if all row sums are equal to the initial square sum.
for i in range(row_start, row_start + square_size):
if row_sums[i][col_start + square_size] - row_sums[i][col_start] != square_sum:
magic = False
break
if not magic:
continue
# Check if all column sums are equal to the initial square sum.
for j in range(col_start, col_start + square_size):
if col_sums[j][row_start + square_size] - col_sums[j][row_start] != square_sum:
magic = False
break
if not magic:
continue
# Check the main diagonal sum.
main_diagonal_sum = 0
for i in range(square_size):
main_diagonal_sum += grid[row_start + i][col_start + i]
if main_diagonal_sum != square_sum:
magic = False
if not magic:
continue
# Check the anti-diagonal sum.
anti_diagonal_sum = 0
for i in range(square_size):
anti_diagonal_sum += grid[row_start + i][col_start + square_size - 1 - i]
if anti_diagonal_sum != square_sum:
magic = False
if magic:
# Once a magic square is found, return the size.
return square_size
return 1
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty grid | Return 0 immediately since no magic square can exist. |
| Grid with only one row or one column | Return 1 if the grid is not empty, as a 1x1 grid is always a magic square. |
| Grid with dimensions [m, n] where m != n and m or n is large | The solution must efficiently iterate through possible square sizes and starting positions, considering the smaller dimension as the maximum possible square size to avoid out-of-bounds access. |
| Grid containing all identical values | The solution should correctly identify the largest possible magic square based on the grid dimensions. |
| Grid containing negative numbers, zeros, and positive numbers | The solution should correctly calculate row, column, and diagonal sums regardless of the sign or value of the numbers. |
| No magic square exists in the grid | The solution should correctly return 0 when no magic square is found after checking all possible sizes and positions. |
| Integer overflow during sum calculations | Use a data type large enough to hold the sums without overflow, such as 'long'. |
| Large grid dimensions leading to excessive computation time | Optimize the solution by using prefix sums for efficient row and column sum calculation to reduce time complexity. |