Linked List Cycle II #19 Most Asked
MediumGiven the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:

Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
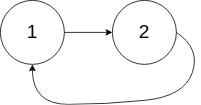
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the linked list be empty or contain only one node?
- Are the values within the linked list nodes bounded by any range or data type (e.g., integers)?
- If a cycle exists, is it guaranteed that all nodes in the list are part of the cycle, or could there be a 'tail' leading into the cycle?
- If multiple nodes could be considered the 'start' of the cycle (depending on which path you take), is there a specific definition I should use to determine the correct starting node?
- Is it possible for a node to point to itself, creating a cycle of length one?
Brute Force Solution
Approach
We're trying to find where a loop starts in a linked list, like figuring out where a merry-go-round begins. The brute force way is simply remembering every place we've been and seeing if we ever come back to one of them. It's like retracing our steps, one by one, until we find a place we've already visited.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the linked list.
- Keep a list of all the places you've already been.
- Go to the next place in the linked list.
- Check if this new place is already in your list of visited places.
- If it is, you've found the start of the loop, so that place is your answer.
- If it's not, add this new place to your list of visited places and go to the next place.
- Keep going until you find a place you've already visited, or until you reach the end of the list (meaning there's no loop).
Code Implementation
def find_linked_list_cycle_start_brute_force(head):
visited_nodes = set()
current_node = head
while current_node:
# If we find current node in the visited nodes, it is the cycle start
if current_node in visited_nodes:
return current_node
# Add the current node to the set of visited nodes
visited_nodes.add(current_node)
# Move to the next node in the linked list
current_node = current_node.next
# If we reach the end of the list, there is no cycle
return NoneBig(O) Analysis
Optimal Solution
Approach
This problem is about finding where a loop starts in a linked list. Instead of checking every possible starting point, we use a clever trick involving two runners to find the loop and then pinpoint its beginning.
Here's how the algorithm would work step-by-step:
- Imagine two runners moving through the linked list, one faster than the other.
- If there's a loop, the faster runner will eventually catch up to the slower runner.
- When they meet, it proves that there's a loop in the list.
- Now, reset one of the runners back to the very beginning of the list, but keep the other runner where they are.
- Move both runners forward at the same speed, one step at a time.
- The point where they meet again is the exact beginning of the loop.
Code Implementation
def find_cycle_start(head):
slow_runner = head
fast_runner = head
while fast_runner and fast_runner.next:
slow_runner = slow_runner.next
fast_runner = fast_runner.next.next
# Detects if a cycle exists
if slow_runner == fast_runner:
# Reset slow runner to head
slow_runner = head
# Move both runners until they meet
while slow_runner != fast_runner:
slow_runner = slow_runner.next
fast_runner = fast_runner.next
#The meeting point is start of cycle.
return fast_runner
# No cycle
return NoneBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty list (head is null) | Return null immediately since there can be no cycle. |
| Single node list (head.next is null) | Return null since a single node cannot form a cycle. |
| Two node list with no cycle (head.next points to null) | The fast and slow pointer will both reach null, causing a null return. |
| Two node list with a cycle (head.next points to head) | The fast and slow pointers will meet at head, and the start of the cycle is head. |
| Cycle includes the head of the list | The algorithm correctly identifies the head as the cycle start. |
| Large list with a cycle far from the head | The algorithm (Floyd's algorithm) scales linearly and will still find the cycle start. |
| Cycle encompasses the entire list | The algorithm correctly identifies the head as the cycle start in this scenario as well. |
| Integer overflow in node values, impacting equality checks (if node values are used for comparison) | The algorithm does not rely on node values; it solely relies on pointer comparisons, so overflow is irrelevant. |