Linked List Cycle

Easy

Yahoo

1 view

Topics:

Linked ListsTwo Pointers

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10⁴].
-10⁵ <= Node.val <= 10⁵
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Linked List Cycle

Easy

Yahoo

1 view

Topics:

Linked ListsTwo Pointers

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

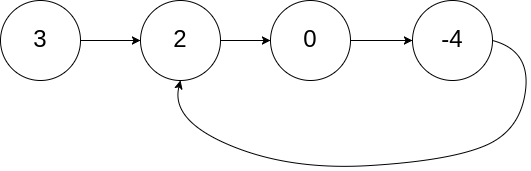
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

The number of the nodes in the list is in the range [0, 10⁴].
-10⁵ <= Node.val <= 10⁵
pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the linked list be empty, or can the head ever be null?
What is the range of values for the node data in the linked list?
Is it possible for a node to point to itself, creating a self-loop?
If there is a cycle, is there a guarantee that all nodes are part of the cycle, or can there be nodes that lead into the cycle but are not themselves part of it?
Are there any memory constraints I should be aware of, considering the size of the linked list?

Brute Force Solution

Approach

Think of the linked list as a train. We want to find out if the train is going in circles. The brute force approach is like checking if we've seen the same car go by before by remembering every car we've seen.

Here's how the algorithm would work step-by-step:

Start at the front of the train (the beginning of the list).
As we go from one car to the next, we write down each car's name (or some kind of ID) in our memory.
Every time we get to a new car, we look back at our list of cars we've already seen.
If we see the current car's name already on our list, it means we've been to this car before and the train is going in a circle!
If we reach the end of the train without seeing any car names repeated, it means the train isn't going in a circle.

Code Implementation

def has_cycle_brute_force(head):
    nodes_seen = set()

    current_node = head

    while current_node:
        # If we've seen the node before, there's a cycle.
        if current_node in nodes_seen:
            return True

        # Store the node in memory.
        nodes_seen.add(current_node)

        current_node = current_node.next

    # If we reach the end without finding a cycle, return False.
    return False

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n²) – We iterate through the linked list of n nodes. For each node, we check if we have seen it before by iterating through a list of previously visited nodes. In the worst-case scenario (no cycle), we will add each node to the seen list and, for each node, iterate through almost all previously visited nodes. This means that for each of the n nodes, we potentially iterate through up to n-1 previously seen nodes, leading to approximately n * (n-1) operations which simplifies to O(n²).

Space Complexity

O(N) – The brute force approach, as described, involves storing the ID of each visited node in memory. This 'list of cars we've already seen' is an auxiliary data structure. In the worst-case scenario, where there is no cycle, we would need to store the IDs of all N nodes in the linked list. Therefore, the space complexity is proportional to N, resulting in O(N) auxiliary space.

Optimal Solution

Approach

The problem is about detecting if a linked list has a cycle (loop). The optimal approach uses two pointers that move at different speeds to detect this cycle without needing extra memory.

Here's how the algorithm would work step-by-step:

Imagine two runners on a track. One runner is fast (moves two steps at a time), and the other is slower (moves one step at a time).
Start both runners at the beginning of the track (linked list).
Have the runners move at their respective speeds, one step and two steps, forward along the track.
If there is a cycle (loop) in the track, the faster runner will eventually catch up to and pass the slower runner.
If the faster runner reaches the end of the track (finds an end without a cycle), then there is no loop.
If at any point the fast runner and the slow runner are at the same place, then there is a cycle.

Code Implementation

def has_cycle(head): 
    if not head: 
        return False

    slow_pointer = head
    fast_pointer = head

    while fast_pointer and fast_pointer.next:
        slow_pointer = slow_pointer.next
        fast_pointer = fast_pointer.next.next

        # Detect the cycle. If they meet, there's a cycle
        if slow_pointer == fast_pointer:
            return True

    # If fast reaches the end, no cycle
    return False

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – The algorithm uses two pointers, 'slow' and 'fast', to traverse the linked list. In the worst-case scenario, where a cycle exists, the 'fast' pointer might traverse the list multiple times before meeting the 'slow' pointer. However, because the 'fast' pointer moves twice as fast as the 'slow' pointer, the number of traversals is directly proportional to the length of the linked list, represented by n. Therefore, the time complexity is O(n).

Space Complexity

O(1) – The algorithm uses two pointers, typically called 'slow' and 'fast', to traverse the linked list. The space required for these pointers is constant, irrespective of the linked list's size (N, where N is the number of nodes in the linked list). No additional data structures like arrays, hash maps, or recursion are used to store intermediate results or track visited nodes. Therefore, the auxiliary space complexity is O(1), indicating constant space usage.

Edge Cases

Case	How to Handle
Empty list (head is null)	Return false immediately since an empty list cannot have a cycle.
List with only one node (head.next is null)	Return false since a single node cannot form a cycle.
List with two nodes and a cycle (head.next points back to head)	Floyd's algorithm (tortoise and hare) correctly detects this case.
Large list with a cycle far from the head	Floyd's algorithm guarantees detection within a reasonable number of steps.
Very long list with no cycle; potential for slow execution	Floyd's algorithm will terminate when the fast pointer reaches the end of the list (null).
List with a cycle that includes the head node	Floyd's algorithm will detect this cycle as the pointers will eventually meet.
List where cycle occurs very close to the tail.	The fast pointer will eventually catch up to the slow pointer within the cycle.
The list contains a self-loop (node points to itself).	Floyd's algorithm will correctly detect this as a cycle since the pointers will immediately meet.