Longest Increasing Path in a Matrix
Longest Increasing Path in a Matrix #1 Most Asked
HardGiven an m x n integers matrix, return the length of the longest increasing path in matrix.
From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).
Example 1:
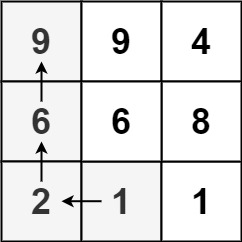
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].
Example 2:
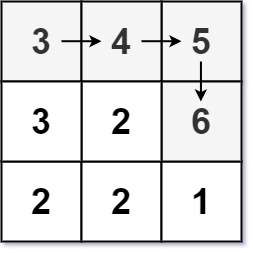
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.
Example 3:
Input: matrix = [[1]] Output: 1
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 231 - 1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix, and what is the maximum possible dimension? What is the range of integer values within the matrix?
- Can the matrix be empty or contain null values? What should I return in these cases?
- What defines a valid path? Can I move diagonally, or only up, down, left, and right?
- If there are multiple longest increasing paths, is it sufficient to return the length of any one of them?
- Is the matrix guaranteed to be rectangular (i.e., all rows have the same number of columns)?
Brute Force Solution
Approach
We are trying to find the longest trail through a grid of numbers, where each number in the trail must be bigger than the last. The brute force approach simply tries every possible trail, starting from every position in the grid.
Here's how the algorithm would work step-by-step:
- Start at any number in the grid.
- From that number, look at each of its neighbors (up, down, left, right).
- If a neighbor is larger than the current number, consider extending the trail to that neighbor.
- For each possible extension of the trail, repeat the process: look at the neighbors of the new number and see if they are larger.
- Keep going, extending the trail in every possible way, until you can't find a larger neighbor to continue with.
- Record the length of that trail.
- Do this process for every single starting number in the grid, trying all possible paths from each starting point.
- Once you've explored all possible trails from every starting number, compare the lengths of all the trails you recorded.
- The longest trail you found is the answer.
Code Implementation
def longest_increasing_path_brute_force(matrix):
if not matrix or not matrix[0]:
return 0
rows = len(matrix)
columns = len(matrix[0])
longest_path = 0
def depth_first_search(row, column, current_length):
nonlocal longest_path
longest_path = max(longest_path, current_length)
# Define possible moves (up, down, left, right)
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for row_direction, column_direction in directions:
new_row = row + row_direction
new_column = column + column_direction
# Check if the new position is within bounds
if 0 <= new_row < rows and 0 <= new_column < columns:
# Check for increasing path condition
if matrix[new_row][new_column] > matrix[row][column]:
depth_first_search(new_row, new_column, current_length + 1)
# Iterate through each cell in the matrix
for row_index in range(rows):
for column_index in range(columns):
# Start DFS from each cell and find the longest path
depth_first_search(row_index, column_index, 1)
return longest_pathBig(O) Analysis
Optimal Solution
Approach
The goal is to find the longest path in a grid where each step increases in value. We avoid recomputing paths by storing the length of the longest path starting from each position. This way, we only compute the longest path for each spot once.
Here's how the algorithm would work step-by-step:
- Go through each spot in the grid.
- For each spot, check its neighbors to see if any of them have a bigger value. If a neighbor has a bigger value, that neighbor is a potential step in an increasing path.
- If there are neighbors with a bigger value, find the longest increasing path that starts at each of those neighbors. Crucially, if we've already calculated the longest path for a neighbor, just use that stored value, instead of recalculating it.
- The longest increasing path from the current spot is one more than the longest increasing path from its best neighbor (the neighbor that gives you the longest path).
- Store the length of the longest increasing path that starts at the current spot, so you don't have to recalculate it later.
- The answer is the biggest of all the longest increasing paths you've found for each spot in the grid.
Code Implementation
def longest_increasing_path(matrix):
if not matrix:
return 0
rows = len(matrix)
cols = len(matrix[0])
longest_path_cache = [[0] * cols for _ in range(rows)]
def depth_first_search(row_index, col_index):
if longest_path_cache[row_index][col_index] != 0:
return longest_path_cache[row_index][col_index]
max_path_length = 1
# Possible directions: up, down, left, right
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
for direction_row, direction_col in directions:
new_row = row_index + direction_row
new_col = col_index + direction_col
if 0 <= new_row < rows and 0 <= new_col < cols and \
matrix[new_row][new_col] > matrix[row_index][col_index]:
# Explore the path from the neighbor
path_length = 1 + depth_first_search(new_row, new_col)
max_path_length = max(max_path_length, path_length)
longest_path_cache[row_index][col_index] = max_path_length
return max_path_length
max_overall_path_length = 0
for row_index in range(rows):
for col_index in range(cols):
# Start DFS from each cell
path_length = depth_first_search(row_index, col_index)
max_overall_path_length = max(max_overall_path_length, path_length)
# The final result is the maximum path length found.
return max_overall_path_lengthBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return 0 immediately as there is no path. |
| Matrix with single row or column | The algorithm should still work correctly, tracing a single path along the row/column. |
| All elements in the matrix are identical | The longest increasing path will have length 1 since no adjacent element is strictly greater. |
| Matrix with all elements in descending order | Each element will be the start of a path of length 1, and algorithm will find the maximum length correctly. |
| Matrix with extremely large dimensions (close to memory limits) | Ensure DFS with memoization avoids stack overflow and the memoization table doesn't exceed memory limits. |
| Matrix with negative numbers and zeros | The algorithm comparing strictly greater numbers works correctly with negative numbers and zeros. |
| Matrix with numbers close to integer limits (Integer.MAX_VALUE, Integer.MIN_VALUE) | The strictly greater than comparison should not cause an integer overflow. |
| Deep recursion stack possible with large path | Memoization should prevent recomputation of paths, limiting the maximum stack depth. |