Longest Univalue Path
MediumGiven the root of a binary tree, return the length of the longest path, where each node in the path has the same value. This path may or may not pass through the root.
The length of the path between two nodes is represented by the number of edges between them.
Example 1:
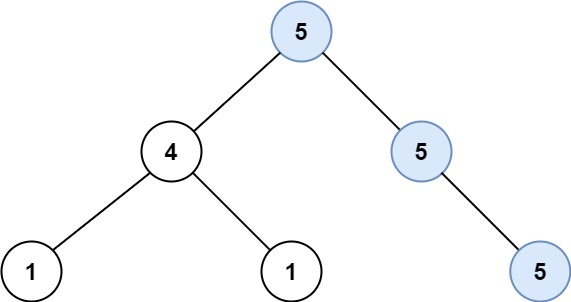
Input: root = [5,4,5,1,1,null,5] Output: 2 Explanation: The shown image shows that the longest path of the same value (i.e. 5).
Example 2:
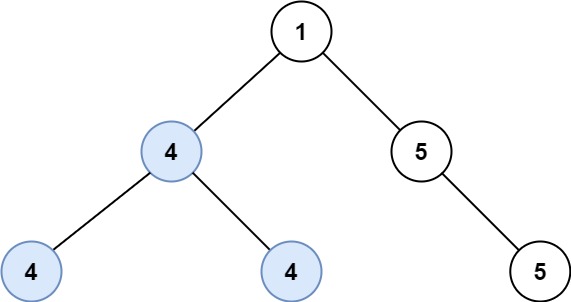
Input: root = [1,4,5,4,4,null,5] Output: 2 Explanation: The shown image shows that the longest path of the same value (i.e. 4).
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -1000 <= Node.val <= 1000- The depth of the tree will not exceed
1000.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty, and if so, what should I return?
- What is the range of possible values for the node values in the tree?
- Does a single node constitute a valid univalue path, and if so, what would its length be?
- If there are multiple univalue paths with the same maximum length, is it acceptable to return the length of any of them?
- Is the tree guaranteed to be a binary search tree, or can it be any binary tree?
Brute Force Solution
Approach
The brute force approach to finding the longest univalue path involves exploring every possible path within the tree. We essentially check every path, regardless of whether it seems promising, to guarantee we find the longest one where all the nodes have the same value. This is done by traversing and comparing values at each point and keeping track of the longest path.
Here's how the algorithm would work step-by-step:
- For every single node in the tree, consider it as the starting point of a possible path.
- From that starting node, explore all possible paths going down the tree.
- For each path, check if all the nodes in the path have the same value as the starting node.
- If a path has all nodes with the same value, record its length.
- Do this for every single node in the tree as a starting point, generating many possible paths.
- After checking all possible paths starting from every node, compare all the recorded path lengths.
- The longest path found among all the checks is the longest univalue path.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def longest_univalue_path_brute_force(root):
longest_path = 0
def get_all_paths_from_node(node):
paths = []
if not node:
return [[]]
left_paths = get_all_paths_from_node(node.left)
right_paths = get_all_paths_from_node(node.right)
for path in left_paths:
paths.append([node.val] + path)
for path in right_paths:
paths.append([node.val] + path)
paths.append([node.val])
return paths
def is_univalue_path(path, node_value):
for node_val in path:
if node_val != node_value:
return False
return True
def calculate_path_length(path):
return len(path) - 1
# Consider each node as start
nodes_to_explore = []
def traverse_tree(node):
if not node:
return
nodes_to_explore.append(node)
traverse_tree(node.left)
traverse_tree(node.right)
traverse_tree(root)
for starting_node in nodes_to_explore:
# explore every possible path
all_paths = get_all_paths_from_node(starting_node)
for path in all_paths:
# Check if all nodes in path have the same value
if is_univalue_path(path, starting_node.val):
path_length = calculate_path_length(path)
# Keep track of the longest path
longest_path = max(longest_path, path_length)
return longest_pathBig(O) Analysis
Optimal Solution
Approach
The goal is to find the longest path in a tree where all the nodes on that path have the same value. We can efficiently find this path by exploring the tree in a specific way, checking the length of potential paths as we go and updating the longest one we've found so far. This eliminates the need to check every single path.
Here's how the algorithm would work step-by-step:
- Imagine you're starting at the top of a tree and working your way down.
- At each branch, you'll check if the value of the branch is the same as its parent.
- If the values are the same, you add one to the current path length. If the values are different, you start a new path of length zero.
- Keep track of the longest path that goes 'down' from each branch. This is the longest path starting at that branch.
- At each branch, also calculate a 'combined' path length. This is the length of the longest path that goes down the left side of the branch, plus the longest path that goes down the right side, plus two (one for each connection to the current branch). This combined path represents a path that passes through the current node.
- As you go, always update the overall longest path you've seen so far. This will either be the longest 'down' path from one of the branches, or a 'combined' path at one of the branches.
- Once you've checked every branch, the overall longest path you've found is the answer.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def longestUnivaluePath(root):
longest_path = 0
def dfs(node):
nonlocal longest_path
if not node:
return 0
left_length = dfs(node.left)
right_length = dfs(node.right)
arrow_left = 0
arrow_right = 0
# Check if extending path to left is possible.
if node.left and node.left.val == node.val:
arrow_left = left_length + 1
# Check if extending path to right is possible.
if node.right and node.right.val == node.val:
arrow_right = right_length + 1
# Update longest path.
longest_path = max(longest_path, arrow_left + arrow_right)
return max(arrow_left, arrow_right)
dfs(root)
return longest_pathBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree (root is null) | Return 0 immediately, as there are no paths in an empty tree. |
| Single node tree | Return 0, as a single node has no edges and thus no path length. |
| Tree with all nodes having the same value | The longest univalue path will traverse the entire tree (if possible), so the algorithm should correctly compute the length of this maximal path. |
| Tree with highly skewed distribution of values (e.g., mostly one value with a few outliers) | The algorithm should still be able to identify the longest univalue path even if most of the tree has the same value and correctly disregard smaller paths with different values. |
| Deeply unbalanced tree (highly skewed structure) | Ensure the recursive calls don't lead to stack overflow errors by considering iterative solutions or tail-call optimization where applicable; most languages will cause a stack overflow in very deep recursions. |
| Large tree (many nodes) | The algorithm's time complexity should be considered to prevent exceeding time limits, aiming for at worst O(N) where N is the number of nodes; Space complexity should also be considered. |
| Tree with no univalue paths (all nodes have different values) | The algorithm should correctly return 0, as there are no univalue paths in this case. |
| Integer overflow if path length is extremely long (unlikely but possible) | Use a data type with sufficient range (e.g., long) to store the path length, or short circuit if this value becomes absurdly large. |