Lowest Common Ancestor of a Binary Tree #7 Most Asked
MediumGiven a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
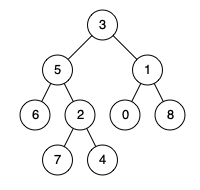
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2 Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary tree be empty, or can p or q be null?
- Are p and q guaranteed to exist in the tree?
- Are the node values unique within the tree, or could there be duplicates?
- Can a node be a descendant of itself, as the problem definition implies?
- If p or q is the root, is the root still considered the lowest common ancestor?
Brute Force Solution
Approach
The brute force method for finding the lowest common ancestor in a family tree involves checking every possible ancestor. We explore all ancestor combinations for the two given individuals until we find the deepest one they share.
Here's how the algorithm would work step-by-step:
- First, find all the ancestors of the first person.
- Then, find all the ancestors of the second person.
- Next, compare the two lists of ancestors to find the ones they have in common.
- Finally, from all the common ancestors, choose the one that is the furthest down the family tree (the deepest). This is the lowest common ancestor.
Code Implementation
def lowest_common_ancestor_brute_force(root, node_one, node_two):
def find_ancestors(node, target, ancestors_list):
if not node:
return False
if node == target:
ancestors_list.append(node)
return True
if find_ancestors(node.left, target, ancestors_list) or \
find_ancestors(node.right, target, ancestors_list):
ancestors_list.append(node)
return True
return False
ancestors_node_one = []
ancestors_node_two = []
find_ancestors(root, node_one, ancestors_node_one)
find_ancestors(root, node_two, ancestors_node_two)
# Need to reverse to find from root to node
ancestors_node_one.reverse()
ancestors_node_two.reverse()
lowest_common_ancestor = None
# Find the common ancestors
for i in range(min(len(ancestors_node_one), len(ancestors_node_two))):
if ancestors_node_one[i] == ancestors_node_two[i]:
lowest_common_ancestor = ancestors_node_one[i]
else:
break
# Return the last common ancestor
return lowest_common_ancestorBig(O) Analysis
Optimal Solution
Approach
The most efficient way to find the lowest common ancestor is to use a method that explores the tree only as needed. We'll use recursion to search for the target nodes and simultaneously identify the common ancestor. The key idea is that if a node has both target nodes in its subtrees, it is the lowest common ancestor.
Here's how the algorithm would work step-by-step:
- Start at the root of the tree.
- For each node, check if it is one of the target nodes we're looking for. If it is, we remember that we've found one of the targets.
- Recursively check the left side of the node to see if it contains either of the target nodes.
- Recursively check the right side of the node to see if it contains either of the target nodes.
- If both the left and right sides contain one of the target nodes, then the current node is the lowest common ancestor. We have found our answer!
- If only one side contains target nodes, pass that side up the chain, meaning the ancestor lies on that side.
- If neither side has target nodes, pass up the signal that no target node was found in this area.
Code Implementation
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def lowestCommonAncestor(root, first_node, second_node):
if not root:
return None
# If the current node is one of the target nodes.
if root == first_node or root == second_node:
return root
left_subtree_result = lowestCommonAncestor(root.left, first_node, second_node)
right_subtree_result = lowestCommonAncestor(root.right, first_node, second_node)
# If both subtrees have a result, this node is the LCA
if left_subtree_result and right_subtree_result:
return root
# If only one subtree has a result, return that result
return left_subtree_result if left_subtree_result else right_subtree_resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Root is null | Return null immediately, as an empty tree has no LCA. |
| p or q is null | Return null if either p or q is null, as LCA is not defined. |
| Tree has only one node (root) | Return the root if root is either p or q; otherwise return null. |
| p and q are the same node | Return p (or q) since a node is an ancestor of itself. |
| p is an ancestor of q | Return p since it is the lowest ancestor containing both. |
| q is an ancestor of p | Return q since it is the lowest ancestor containing both. |
| p or q is not in the tree | The standard recursive solution will still function correctly, ultimately returning null if only one or neither node is found by the search. |
| Skewed Tree (left or right) | The solution should still work correctly, though the recursive calls might take longer to complete in a highly skewed tree. |