Manhattan Distances of All Arrangements of Pieces

Hard

Rubrik

8 views

Topics:

ArraysGreedy Algorithms

You are given three integers m, n, and k.

There is a rectangular grid of size m × n containing k identical pieces. Return the sum of Manhattan distances between every pair of pieces over all valid arrangements of pieces.

A valid arrangement is a placement of all k pieces on the grid with at most one piece per cell.

Since the answer may be very large, return it modulo 10⁹ + 7.

The Manhattan Distance between two cells (x_i, y_i) and (x_j, y_j) is |x_i - x_j| + |y_i - y_j|.

Example 1:

Input: m = 2, n = 2, k = 2

Output: 8

Explanation:

The valid arrangements of pieces on the board are:

In the first 4 arrangements, the Manhattan distance between the two pieces is 1.
In the last 2 arrangements, the Manhattan distance between the two pieces is 2.

Thus, the total Manhattan distance across all valid arrangements is 1 + 1 + 1 + 1 + 2 + 2 = 8.

Example 2:

Input: m = 1, n = 4, k = 3

Output: 20

Explanation:

The valid arrangements of pieces on the board are:

The first and last arrangements have a total Manhattan distance of 1 + 1 + 2 = 4.
The middle two arrangements have a total Manhattan distance of 1 + 2 + 3 = 6.

The total Manhattan distance between all pairs of pieces across all arrangements is 4 + 6 + 6 + 4 = 20.

Constraints:

1 <= m, n <= 10⁵
2 <= m * n <= 10⁵
2 <= k <= m * n

Try coding it in LeetCode

Manhattan Distances of All Arrangements of Pieces

Hard

Rubrik

8 views

Topics:

ArraysGreedy Algorithms

You are given three integers m, n, and k.

There is a rectangular grid of size m × n containing k identical pieces. Return the sum of Manhattan distances between every pair of pieces over all valid arrangements of pieces.

A valid arrangement is a placement of all k pieces on the grid with at most one piece per cell.

Since the answer may be very large, return it modulo 10⁹ + 7.

The Manhattan Distance between two cells (x_i, y_i) and (x_j, y_j) is |x_i - x_j| + |y_i - y_j|.

Example 1:

Input: m = 2, n = 2, k = 2

Output: 8

Explanation:

The valid arrangements of pieces on the board are:

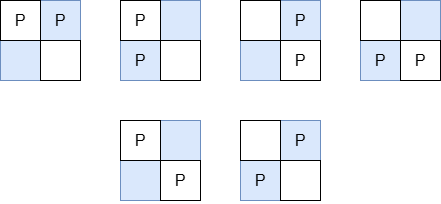
In the first 4 arrangements, the Manhattan distance between the two pieces is 1.
In the last 2 arrangements, the Manhattan distance between the two pieces is 2.

Thus, the total Manhattan distance across all valid arrangements is 1 + 1 + 1 + 1 + 2 + 2 = 8.

Example 2:

Input: m = 1, n = 4, k = 3

Output: 20

Explanation:

The valid arrangements of pieces on the board are:

The first and last arrangements have a total Manhattan distance of 1 + 1 + 2 = 4.
The middle two arrangements have a total Manhattan distance of 1 + 2 + 3 = 6.

The total Manhattan distance between all pairs of pieces across all arrangements is 4 + 6 + 6 + 4 = 20.

Constraints:

1 <= m, n <= 10⁵
2 <= m * n <= 10⁵
2 <= k <= m * n

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the data types and ranges for the x and y coordinates of the pieces? Can they be negative, zero, or floating-point numbers?
How many pieces can there be at most? Should I consider potential integer overflow when calculating Manhattan distances or summing them?
If the input list of pieces is empty or contains only one piece, what should the function return?
Are the pieces guaranteed to have distinct coordinates, or can there be duplicate (x, y) pairs?
Is the order of the arrangements significant? Do I need to return all permutations in a specific order or just the sum of Manhattan distances for each arrangement?

Brute Force Solution

Approach

The brute force approach involves trying every possible arrangement of pieces on the board. For each arrangement, we calculate the total Manhattan distance and keep track of the minimum we find across all arrangements. It's like trying every possible layout to find the one with the smallest distance.

Here's how the algorithm would work step-by-step:

Consider all possible orders for placing the pieces on the board. This means trying every possible combination of piece positions.
For each arrangement (combination of piece positions), calculate the Manhattan distance between every pair of pieces.
Sum up all the individual Manhattan distances to get a total distance for that specific arrangement.
Compare the total distance of this arrangement to the smallest total distance we've found so far. If the current arrangement's total distance is smaller, we remember it as the new smallest distance.
Repeat this process for every single possible arrangement of pieces.
After considering all arrangements, the smallest total Manhattan distance that we remembered is the answer.

Code Implementation

import itertools

def manhattan_distance(point_one, point_two):
    return abs(point_one[0] - point_two[0]) + abs(point_one[1] - point_two[1])

def total_manhattan_distance(arrangement):
    total_distance = 0
    number_of_pieces = len(arrangement)
    for i in range(number_of_pieces):
        for j in range(i + 1, number_of_pieces):
            total_distance += manhattan_distance(arrangement[i], arrangement[j])
    return total_distance

def find_min_manhattan_distance_brute_force(piece_positions):
    # Initialize minimum distance to infinity.
    minimum_total_distance = float('inf')

    # Generate all possible arrangements of piece positions.
    all_arrangements = list(itertools.permutations(piece_positions))

    # Iterate through all arrangements.
    for arrangement in all_arrangements:
        # Calculate total Manhattan distance for current arrangement.
        current_total_distance = total_manhattan_distance(arrangement)

        # Update minimum distance if current distance is smaller.
        if current_total_distance < minimum_total_distance:
            minimum_total_distance = current_total_distance

    return minimum_total_distance

Big(O) Analysis

Time Complexity

O(n!) – The problem considers all possible arrangements (permutations) of the pieces on the board. With n pieces, there are n! (n factorial) possible arrangements to evaluate. For each of these arrangements, we need to calculate the Manhattan distance between every pair of pieces. There are n choose 2, or n(n-1)/2, pairs of pieces. Although calculating the distances is O(n^2) for each arrangement, the dominant factor is iterating through all n! arrangements. Therefore, the overall time complexity is O(n!).

Space Complexity

O(N) – The brute force approach considers all possible arrangements of pieces. To generate these arrangements, it implicitly uses a recursive algorithm or a similar method to store the current arrangement of pieces. This storage requires memory proportional to the number of pieces, where N represents the number of pieces. Therefore, the algorithm needs auxiliary space to hold the current arrangement during the permutation generation, resulting in O(N) space complexity due to the call stack or temporary storage for each arrangement during generation. Also, we are using a min variable to store the smallest total distance found so far, but it only takes up constant space and is dominated by the arrangement storage.

Optimal Solution

Approach

The problem asks us to find the total Manhattan distance for every possible arrangement of pieces. Instead of generating every arrangement and calculating its Manhattan distance (which would take way too long), we can cleverly use math and combinatorics to figure out the total distance efficiently.

Here's how the algorithm would work step-by-step:

Realize that the total Manhattan distance is just the sum of the absolute differences in the x-coordinates plus the sum of the absolute differences in the y-coordinates across all arrangements.
Focus on the x-coordinates first. For each pair of pieces, calculate the difference in their x-coordinates.
Determine how many times this specific pair of pieces will be arranged in opposite orders. The key insight is that each unique pair appears in (total arrangements) / (number of pairs) arrangements.
Multiply the x-coordinate difference by the number of times the pair is swapped. This gives the total contribution of that pair's x-coordinate difference to the overall Manhattan distance.
Repeat the above process for every pair of pieces.
Sum up these contributions to get the total Manhattan distance contributed by the x-coordinates.
Now, do the exact same process for the y-coordinates.
Finally, add the total Manhattan distance from the x-coordinates to the total Manhattan distance from the y-coordinates to get the overall answer.

Code Implementation

def manhattan_distances(coordinates):
    number_of_pieces = len(coordinates)
    total_arrangements = 1
    for i in range(1, number_of_pieces + 1):
        total_arrangements *= i

    total_manhattan_distance = 0
    # Calculate Manhattan distance for x coordinates.
    x_coordinates = [x for x, y in coordinates]
    total_manhattan_distance += calculate_coordinate_distance(x_coordinates, total_arrangements)
    
    # Calculate Manhattan distance for y coordinates.
    y_coordinates = [y for x, y in coordinates]
    total_manhattan_distance += calculate_coordinate_distance(y_coordinates, total_arrangements)

    return total_manhattan_distance

def calculate_coordinate_distance(coordinate_list, total_arrangements):
    number_of_pieces = len(coordinate_list)
    total_coordinate_distance = 0

    # Iterate through all pairs of pieces.
    for i in range(number_of_pieces):
        for j in range(i + 1, number_of_pieces):
            # Calculate coordinate difference for the pair.
            coordinate_difference = abs(coordinate_list[i] - coordinate_list[j])

            #Calculate how many times the pair will be swapped.
            number_of_swaps = total_arrangements // (number_of_pieces * (number_of_pieces - 1) // 2)

            # Accumulate the distance
            total_coordinate_distance += coordinate_difference * number_of_swaps
    
    return total_coordinate_distance

Big(O) Analysis

Time Complexity

O(n²) – The algorithm iterates through all pairs of pieces to calculate the Manhattan distance contribution of each pair. The dominant operation is comparing each piece with every other piece. Given n pieces, the number of pairs is proportional to n * (n - 1) / 2. This quadratic relationship makes the time complexity O(n²), where n is the number of pieces.

Space Complexity

O(1) – The algorithm iterates through pairs of pieces, calculating differences and contributions to the total Manhattan distance. No auxiliary data structures are used to store intermediate results or arrangements of the pieces. Only a few variables for storing sums and differences are used, resulting in constant auxiliary space, independent of the number of pieces N.

Edge Cases

Case	How to Handle
Null or empty input array	Return an empty list or an appropriate error code indicating invalid input to prevent null pointer exceptions or incorrect calculations.
Array with only one piece	Return an empty list since no pairs can be formed to calculate Manhattan distances.
All pieces located at the same coordinate	The Manhattan distance between all pairs will be 0, which the algorithm should correctly compute.
Maximum array size leading to integer overflow during distance calculation	Use a larger data type (e.g., long) for distance calculations to prevent integer overflow if Manhattan distance can exceed the maximum value of int.
Very large coordinate values leading to integer overflow	Use long data types for storing coordinates or implement overflow checks during distance calculation.
Duplicate piece positions	The permutation logic should handle duplicate piece positions correctly by generating all distinct arrangements regardless of duplicates.
Large number of pieces causing the permutation generation to become extremely slow	The algorithm's time complexity is factorial, so for large input sizes, return an error message/null value after exceeding a set number of recursions or implement an approximate heuristic if an exact solution isn't strictly required.
Negative coordinate values	The Manhattan distance calculation \|x1-x2\| + \|y1-y2\| handles negative coordinates correctly without requiring special treatment.