Max Points on a Line
Max Points on a Line #1 Most Asked
HardGiven an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.
Example 1:
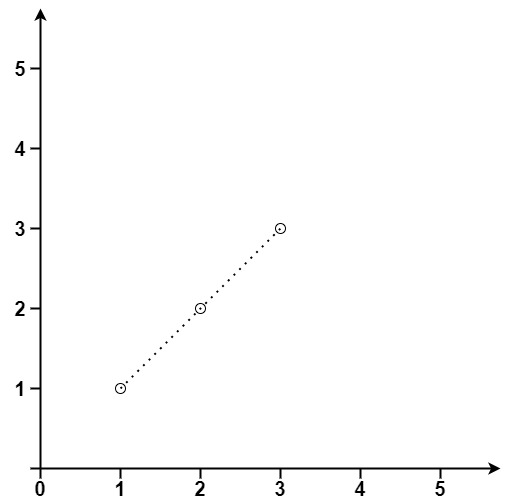
Input: points = [[1,1],[2,2],[3,3]] Output: 3
Example 2:
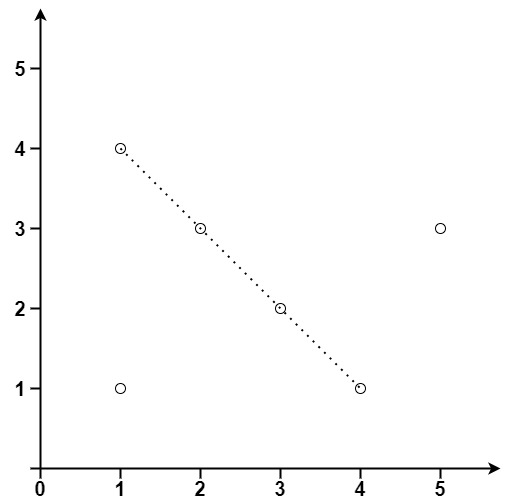
Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]] Output: 4
Constraints:
1 <= points.length <= 300points[i].length == 2-104 <= xi, yi <= 104- All the
pointsare unique.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Are the point coordinates guaranteed to be integers, or could they be floating-point numbers? If floats, what is the precision I should consider?
- What are the constraints on the number of points in the input array? Can it be empty, or contain just one point?
- Are duplicate points allowed in the input array? If so, how should they be handled (e.g., do they all count towards the line's total)?
- Should I consider lines that are perfectly vertical (infinite slope)? If so, how should I represent or handle them in my calculations?
- If multiple lines have the same maximum number of points, does it matter which one I return, or is any one of them acceptable?
Brute Force Solution
Approach
We want to find the maximum number of points that lie on the same straight line. The brute force approach involves checking every possible line that can be formed by any two points and then counting how many other points fall on that specific line.
Here's how the algorithm would work step-by-step:
- Pick any two points from the given collection.
- Imagine a straight line passing through these two chosen points.
- Now, go through all the other points one by one.
- For each other point, check if it perfectly sits on the imaginary line you just drew.
- Keep a count of how many points lie on this particular line, including the initial two.
- Record this count.
- Repeat this entire process for every unique pair of points you can select from the collection.
- After checking all possible pairs and their corresponding lines, find the largest count you recorded. This largest count represents the maximum number of points on a single line.
Code Implementation
def max_points_on_a_line_brute_force(points):
number_of_points = len(points)
if number_of_points < 3:
return number_of_points
maximum_points_on_line = 0
# Iterate through every possible pair of points to define a line.
for first_point_index in range(number_of_points):
for second_point_index in range(first_point_index + 1, number_of_points):
current_points_on_line = 0
point_one_x = points[first_point_index][0]
point_one_y = points[first_point_index][1]
point_two_x = points[second_point_index][0]
point_two_y = points[second_point_index][1]
# Determine the line's equation parameters (slope and intercept or handle vertical lines).
if point_one_x == point_two_x:
# This is a vertical line.
for third_point_index in range(number_of_points):
if points[third_point_index][0] == point_one_x:
current_points_on_line += 1
else:
# Calculate slope and intercept for non-vertical lines.
slope = (point_two_y - point_one_y) / (point_two_x - point_one_x)
intercept = point_one_y - slope * point_one_x
for third_point_index in range(number_of_points):
point_three_x = points[third_point_index][0]
point_three_y = points[third_point_index][1]
# Check if the third point lies on the line defined by the first two.
if abs(point_three_y - (slope * point_three_x + intercept)) < 1e-9:
current_points_on_line += 1
maximum_points_on_line = max(maximum_points_on_line, current_points_on_line)
return maximum_points_on_lineBig(O) Analysis
Optimal Solution
Approach
The most efficient way to solve this is to consider each point as a potential anchor and then figure out how many other points lie on the same line passing through it. We can do this by looking at the 'slope' or 'direction' each other point takes relative to the anchor point.
Here's how the algorithm would work step-by-step:
- Pick a single point and imagine it's the starting point of many potential lines.
- For every other point, calculate the direction it goes from the chosen starting point. Think of this direction as a unique signature for the line it would form with the starting point.
- Keep track of how many other points share the exact same direction signature from our starting point. This tells us how many points are on that particular line.
- If two points are exactly on top of each other, count them separately for lines that start from different original points.
- After checking all other points against our chosen starting point, find the direction that had the most points.
- Add our initial starting point to that count, as it's also on that line.
- Repeat this entire process, making each point in turn the starting point.
- The largest line count you find across all the starting points is your answer.
Code Implementation
import math
def max_points_on_a_line(points):
number_of_points = len(points)
if number_of_points <= 2:
return number_of_points
maximum_points_on_line = 0
for starting_point_index in range(number_of_points):
slope_counts = {}
duplicate_points_count = 1
current_maximum_points = 0
anchor_point_x = points[starting_point_index][0]
anchor_point_y = points[starting_point_index][1]
for other_point_index in range(starting_point_index + 1, number_of_points):
other_point_x = points[other_point_index][0]
other_point_y = points[other_point_index][1]
# Handle cases where points are identical to correctly count them.
if anchor_point_x == other_point_x and anchor_point_y == other_point_y:
duplicate_points_count += 1
continue
delta_x = other_point_x - anchor_point_x
delta_y = other_point_y - anchor_point_y
# Simplify the slope by finding the greatest common divisor.
if delta_x == 0:
slope_signature = (float('inf'),)
elif delta_y == 0:
slope_signature = (0,)
else:
common_divisor = math.gcd(delta_x, delta_y)
slope_signature = (delta_y // common_divisor, delta_x // common_divisor)
slope_counts[slope_signature] = slope_counts.get(slope_signature, 0) + 1
current_maximum_points = max(current_maximum_points, slope_counts[slope_signature])
# The total points for a line include the anchor and any duplicates.
maximum_points_on_line = max(maximum_points_on_line, current_maximum_points + duplicate_points_count)
return maximum_points_on_line
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input array is null or empty | If the input array is null or has fewer than 1 point, return 0 as no line can be formed. |
| Input array contains only one point | If there's only one point, it lies on a line by itself, so return 1. |
| All points are identical | The algorithm should correctly count all identical points as being on the same line by handling duplicate points appropriately. |
| All points lie on a vertical line | A special check for vertical lines (infinite slope) must be implemented using a distinct counter or by handling division by zero. |
| All points lie on a horizontal line | Horizontal lines have a slope of 0, which should be handled correctly by the slope calculation logic. |
| Floating point precision issues when calculating slopes | Using fractions or Greatest Common Divisor (GCD) to represent slopes helps avoid floating-point inaccuracies. |
| Large number of points leading to inefficient runtime | The O(n^2) complexity of iterating through pairs and calculating slopes is generally acceptable for typical interview constraints, but extremely large inputs might require optimization research. |
| Points with zero coordinates or negative coordinates | The slope calculation formula works correctly with zero and negative coordinates, as long as division by zero is handled for vertical lines. |