Maximal Square
Maximal Square #9 Most Asked
MediumGiven an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
Example 1:
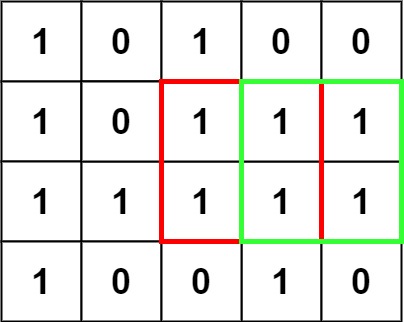
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 4
Example 2:
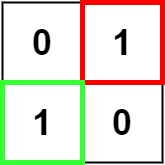
Input: matrix = [["0","1"],["1","0"]] Output: 1
Example 3:
Input: matrix = [["0"]] Output: 0
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]is'0'or'1'.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the input matrix? Can it be empty or contain empty rows?
- Are the elements of the matrix guaranteed to be only '0' or '1', or could there be other characters?
- If the matrix contains no '1's, what should be returned as the area of the largest square?
- Can the matrix be very large, such that memory constraints might be a concern for certain approaches?
- Is it possible to have a matrix with only one row or one column?
Brute Force Solution
Approach
We want to find the largest square made entirely of '1's within a grid of '0's and '1's. The brute force method involves checking every single possible square within the grid to see if it's a valid maximal square.
Here's how the algorithm would work step-by-step:
- Consider every possible top-left corner for a square in the grid.
- For each potential top-left corner, imagine squares of increasing size, starting from a tiny one by one square.
- For each imagined square, check if all the cells it covers in the grid are '1's.
- If a square is completely filled with '1's, remember its size.
- Continue expanding the square from that same top-left corner, checking larger and larger sizes, until you either hit the edge of the grid or find a cell that is a '0'.
- After checking all possible square sizes for that specific top-left corner, move on to the next potential top-left corner and repeat the process.
- Keep track of the largest valid square you've found throughout all these checks.
- The size of the largest valid square you recorded at the end is your answer.
Code Implementation
def maximal_square_brute_force(matrix):
if not matrix or not matrix[0]:
return 0
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
maximum_square_side = 0
# Iterate through every cell to consider it as a potential top-left corner
for top_left_row_index in range(number_of_rows):
for top_left_column_index in range(number_of_columns):
# Start checking for squares of increasing size from this corner
for side_length in range(1, min(number_of_rows - top_left_row_index, number_of_columns - top_left_column_index) + 1):
is_valid_square = True
# Check if all cells within the current square are '1's
for row_offset in range(side_length):
for column_offset in range(side_length):
current_row = top_left_row_index + row_offset
current_column = top_left_column_index + column_offset
if matrix[current_row][current_column] == '0':
is_valid_square = False
break
if not is_valid_square:
break
# If the current square is valid, update the maximum side length found
if is_valid_square:
maximum_square_side = max(maximum_square_side, side_length)
else:
# If a square of this size is not valid, larger squares from this corner won't be either
break
return maximum_square_side * maximum_square_sideBig(O) Analysis
Optimal Solution
Approach
This problem asks us to find the largest square composed entirely of '1's within a grid of '0's and '1's. The optimal strategy involves a dynamic programming approach, where we build up the solution by looking at smaller subproblems. Essentially, we figure out the size of the largest square ending at each position based on the sizes of squares ending at its immediate neighbors.
Here's how the algorithm would work step-by-step:
- Imagine a helper grid where each cell will store the size of the largest square that has this cell as its bottom-right corner.
- If a cell in the original grid is a '0', then no square can end there, so the corresponding cell in our helper grid gets a '0'.
- If a cell in the original grid is a '1', then a square of at least size 1 can end there. We then look at the cells immediately above, to the left, and diagonally above-left in our helper grid.
- The size of the largest square ending at the current '1' cell is one more than the smallest size found in those three neighboring helper cells. This is because to form a larger square, all three neighbors must also be the bottom-right corner of squares that can combine.
- We keep track of the biggest size we encounter across all cells in the helper grid as we fill it.
- Once the entire helper grid is filled, the largest size we recorded is the side length of the maximal square. We then square this side length to get the area.
Code Implementation
def maximalSquare(matrix):
if not matrix:
return 0
rows_count = len(matrix)
columns_count = len(matrix[0])
# Initialize a DP table to store the size of the largest square ending at each cell.
dp_table = [[0] * (columns_count + 1) for _ in range(rows_count + 1)]
max_side_length = 0
# Iterate through the matrix, filling the DP table.
for row_index in range(1, rows_count + 1):
for column_index in range(1, columns_count + 1):
if matrix[row_index - 1][column_index - 1] == '1':
# To form a larger square, all three neighbors must also be part of a square.
dp_table[row_index][column_index] = min(
dp_table[row_index - 1][column_index], # Top neighbor
dp_table[row_index][column_index - 1], # Left neighbor
dp_table[row_index - 1][column_index - 1] # Diagonal top-left neighbor
) + 1
# Update the maximum side length found so far.
max_side_length = max(max_side_length, dp_table[row_index][column_index])
# The result is the area of the largest square.
return max_side_length * max_side_lengthBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty or null input matrix | The solution should return 0 area immediately if the input matrix is null or has zero rows or zero columns. |
| Matrix with only one row or one column | A 1xN or Nx1 matrix can only contain squares of size at most 1x1, so the maximum area will be 1 if any '1' exists, otherwise 0. |
| Matrix contains only '0's | If no '1's are present, no square of '1's can be formed, resulting in a maximum area of 0. |
| Matrix contains only '1's | The largest square will be bounded by the dimensions of the matrix itself, with its area being min(rows, columns)^2. |
| Matrix is a single cell (1x1) | If the cell contains '1', the area is 1; if it contains '0', the area is 0. |
| Large input matrix dimensions | A dynamic programming approach with O(m*n) time and space complexity efficiently handles large matrices within typical memory limits. |
| No valid square of size greater than 1x1 exists | The algorithm correctly identifies and returns 1 as the maximum area if only isolated '1's exist. |
| All '1's form a single large square covering most of the matrix | The dynamic programming approach will correctly propagate the size of the square to cover the entire valid region. |